Оглавление:


Моменты инерции сложных сечений
- Момент инерции сложного сечения В вычислительной практике часто приходится рассчитывать момент инерции сложных сечений для различных осей в плоскости фигуры. Для стандартного
поперечного сечения стержня-угловой биссектрисы (рис. 21, А) и неравенство (рис. 21, б), двутавровая балка (фиг. 21, б), канал (фиг. 21, г) — момент инерции для разных осей ГОСТ8509-72、
8510-72、8239-72*、8240-72、он указан в таблице вместе с размерами, Людмила Фирмаль
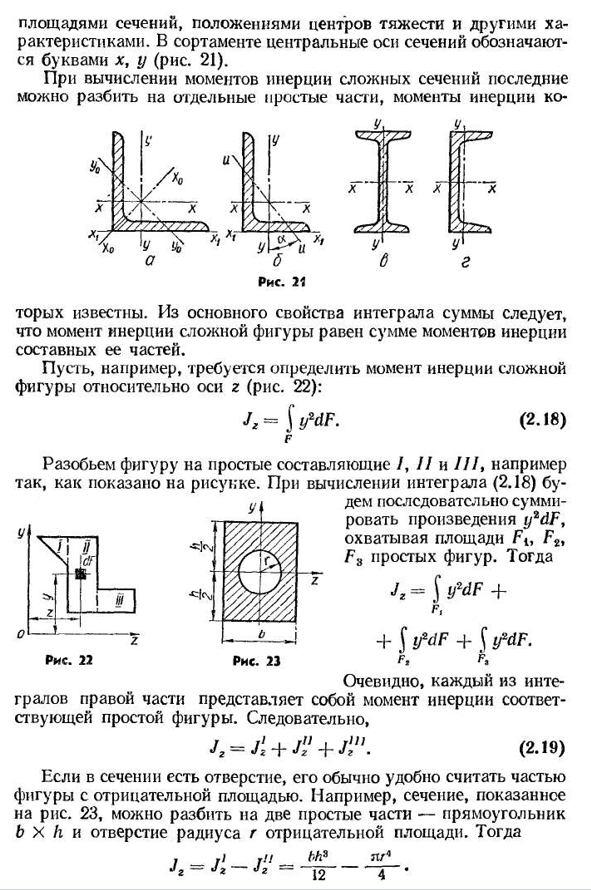
19 площадь поперечного сечения, расположение центра тяжести и другие характеристики. В этом ассортименте центральная ось сечения обозначена буквой x, y(рис. 21). При расчете момента инерции для сложного участка последний можно разделить
на отдельные простые части, моменты инерции. Закон известен. Момент инерции сложной фигуры получается из базисного характера полного интеграла, который равен сумме моментов инерции ее составных частей. Например, предположим, что требуется определить момент инерции сложной фигуры относительно оси Z.
- 22): L=J y * dF. (2.18)Ф Например, Давайте разделим фигуру на простые компоненты/, II и I I/, как показано на рисунке. При вычислении интеграла (2.18)БУ Двадцать три риса. dem последовательно
суммирует произведение y2dF. Fi, F2, F3 покрывает простой квадрат формы. Тогда Jz=f yMF+ ФФ +ТФД ф ф+ф ifdF. Очевидно, что каждый из интегралов правой части представляет момент инерции соответствующей простой фигуры. И так оно и есть., (2.19) Если в разрезе имеются отверстия, то обычно полезно
рассматривать их как часть фигуры в отрицательной области. Например, разрез, Людмила Фирмаль
показанный на рисунке. 23 можно разделить на две простые части-прямоугольник B X h и отверстие радиуса g в отрицательной области. Затем j_—J2 — 12 4″’ —
Смотрите также:
| Статические моменты площади. центр тяжести площади | Моменты инерции относительно параллельных осей |
| Моменты инерции плоских фигур | Зависимости между моментами инерции при повороте координатных осей |

