Оглавление:




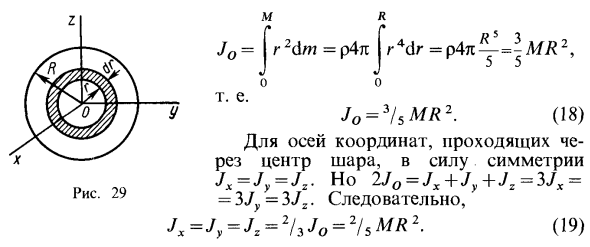

Моменты инерции простейших однородных тел
- Момент инерции объекта сложной формы часто можно рассчитать, если он был предварительно разделен на объекты простой формы. Момент инерции сложного объекта получается суммированием моментов инерции этих частей объекта. Получите формулу для расчета момента инерции некоторых однородных простых объектов. Однородный стержень Есть стержень с одинаковой длиной I и массой M (рис. 25). Сориентируйте быка на стержень вдоль оси.
Рассчитайте момент инерции стержня относительно оси Oz, которая проходит перпендикулярно от конца стержня к стержню. Согласно определению момента инерции континуума вокруг оси, Рисунок 25 JOl-f x2dm = p j x2dx. Поскольку dw = pdx, p = M / l — плотность стержня. При расчете интеграла это выглядит так Вот так Момент инерции стержня относительно оси Cz ‘, проходящей через центр тяжести и параллельный оси Oz, определяется по теореме Штейнера. Jo ^ Jc. + Md1 d2 = (// 2) 2 = / 2/4 Это (12) Прямоугольная плита Размеры прямоугольной тонкой пластины — f и h, а масса — M (рисунок 26). Оси Ox и Oy находятся в плоскости пластины, а оси Oz перпендикулярны ей.
В общем случае все шесть уравнений можно рассматривать вместе, так как правая часть этих уравнений зависит от шести параметров и их начальных производных, если сила зависит от скорости. Людмила Фирмаль
Чтобы определить момент инерции пластины относительно оси Oy, разбейте пластину на основные полосы шириной d.v и массой dwi = pAdx и интегрируйте x от 0 до /. получить Потому что фи = М Выполняя тот же расчет для оси Ox, • ‘.- «и- Эта ось Вол проходит через центр пластины. Определить момент инерции Для оси Oz необходимо сначала вычислить момент инерции одиночной заштрихованной полосы для параллельной оси O’z согласно уравнению стержня (12), а затем применить теорему Штейнера. Для основных полос, Формула интеграции Получить в диапазоне от 0 до I Относительно блюдо.
Поэтому следующая формула получается для момента инерции пластины относительно оси координат. L-AND ^; (13> Круглый диск Существует тонкий однородный диск с радиусом R и массой M (с.27). Рассчитаем момент инерции Джо для точки О. Этот момент инерции тонкого диска совпадает с моментом инерции Jz относительно координатной оси Oz, перпендикулярной плоскости диска. Разделите диск на концентрические полосы шириной dr и ограничьте их в виде материальных кругов. Масса полосы равна плотности p = M / (nR2), т.е. d / u = p-2nrdr, в 2nrdr раз больше ее площади.
- Момент одной полосы относительно точки O равен r2at. Обо всем диске Jo = Jr2dwi = p-2l Jr’dr = p-2l ^ — Вот так. T / Z Tiz Рис. 28 Jt = J0 = MR2! 2. (14) Для координатных осей Ox и Oy в плоскости диска с симметрией Jx = Jr, используя (8) = = JX + Jy + Jz, но Jz-J0 Jx = Jy = ll2Jo = MR2l ^. (15) Для тонких проволочных колец или круглых колес масса распределяется по всему ободу, а не по всей площади. Jt = Jo = MR2-, Jz = Jy = l! 2mr2. (16) Круглый цилиндр Для круглого однородного цилиндра с массой M, радиусом R и длиной I (рис. 28) сначала рассчитайте момент инерции относительно оси симметрии Oz. Для этого мы нарушаем Цилиндр на тонком диске массой dm и толщиной dz с плоскостью, перпендикулярной оси Oz.
Для таких дисков момент Это J. = MR2! 2. (17) Рассчитывается момент инерции относительно поперечной оси Su цилиндра. Для этого цилиндр с поперечным сечением, перпендикулярным вертикальной оси, делится на основные диски толщиной dz. Согласно теореме Штейнера dmR + dmz2, момент инерции основного диска с массой d / u = lL 2pdz относительно оси Si. Чтобы получить момент инерции всего цилиндра вокруг оси Su, полученное выражение должно быть интегрировано по z в диапазоне от 0 до // 2, а результат должен быть удвоен. получить Однако nR2lp = M — масса цилиндра. В результате 7Cy = L / (d2 / 4 + / 2/12).
Прежде чем рассматривать применение некоторой теоремы Карно, необходимо рассчитать кинетическую энергию потерянной скорости твердого тела, движущегося вокруг неподвижной оси или неподвижной точки. Людмила Фирмаль
Таким образом, момент инерции цилиндра относительно его симметричной горизонтальной оси получается как сумма моментов инерции диска и стержня относительно этой оси, масса которых равна массе цилиндра в отдельности. Диск получается из цилиндра симметричным сжатием с обоих концов до средней плоскости при сохранении радиуса и получается путем сжатия стержня-цилиндра до однородного стержня вдоль оси цилиндра при сохранении длины. Мяч Масса шара равна М, а радиус равен R (рис. 29).
Делит шар на концентрические сферические слои с радиусом r и толщиной Слой равен произведению площади поверхности сферы радиуса r на толщину слоя dr, т.е. dK = 4nr2dr. Следовательно, масса базового слоя равна dm = pd V = p4lg 2dr. Для момента инерции шара относительно центра O шара, Рисунок 29 Jo = Jr2dzn = р4лJ r4dr = р4л ^ — = ^ Л / Я2, _ Т. е. JO = 3! SMR2. (18) Для координатной оси, проходящей через центр шара, из-за симметрии, jx = jy = jz, но 2JO = JX + J „+ JI = 3JX = 3Jy = 3JX. Jx = Jy = Jz = 2/3 Jo = 2 / sMR2. (19)
Смотрите также:
Задачи по теоретической механике
| Моменты инерции относительно осей координат | Однородный стержень |
| Теорема о моментах инерции относительно параллельных осей (теорема Штейнера) | Прямоугольная пластина |

