Оглавление:



Моменты инерции
- Момент инерции Осевой момент инерции области называется выражением вида Показать интеграл Jy = j zadF; Jz = §y2dF, F F Jyz = §yzdF F (13.3) (13L) Он называется центробежным моментом инерции в области вокруг оси y и оси r. Полярный момент инерции Ja = J P2dF F
(Обратитесь к рисунку 13.4 для выражений (13.3) — (13.5)). Вал и полярный момент инерции Jp = Jy + / g * У 2-256 (13.5) (13,6) 249
Момент инерции измеряется в см4. Определение момента инерции базового Людмила Фирмаль
узла не распространяется на конечную область, но если вы примените теорему о среднем значении к интегралу (13.3), вы можете написать: = tyl J z-i 2z F, (13.7) где iy и iz — радиус инерции области
относительно оси y и оси z (размеры в см). Количество акций и альтернативное количество акций N и I примерно равны rd, n и t (рисунок 13.4). 1. Для параллельного переноса координатных осей: 4 = 4 e + ^ 2; ^ = ^ c + w; J yug — Jyczc ~ ^ ~ Fab ‘(13,9) Где J, J, J, J и J — моменты
- инерции, соответствующие центральной оси (начало центра тяжести области), параллельной оси y. a и b — расстояние между осью y и усами, z и zc. с0 — расстояние между началом координат системы координат и уссгами. 2. Когда ось вращается на угол a: Jy = Jy cos3а-ф-Jgsin3 a-Jzy sin 2a; 7g = Jy 8 * n2 a + J g cos2 a + Jzy sin 2a; = ‘Jy 2 S’n 2 “Jyz C0S 2” ’ (13.10) Где J., J и J — моменты инерции относительно оси t / j nzj, и они вращаются против часовой стрелки на угол a относительно осей y и z. Общий момент инерции в осевом направлении при
вращении вала не изменяется. J ^ i + ~ Jу + Jz- (13.11) Момент инерции (центробежный момент инерции) сложной формы определяется как сумма моментов инерции (центробежный момент инерции) узлов компонентов (рис. 13.5). В этом случае используется формула перехода по параллельной оси (13.9): р р р Jy = X J YI + f 1a b J 2-5l Jyz-S J A’jZ; + (13.12) i = l / = 1 i = n Где я номер сайта (я = вся область, J „и /, ,,, «Я г 1 Пройдите через эту (tth) позицию платформы, центр тяжести 1, 2, 3, …, n) относительно осей t /, -, z. n — количество сайтов,
которые нужно разделить. ..- Момент инерции и инертный центробежный момент Людмила Фирмаль
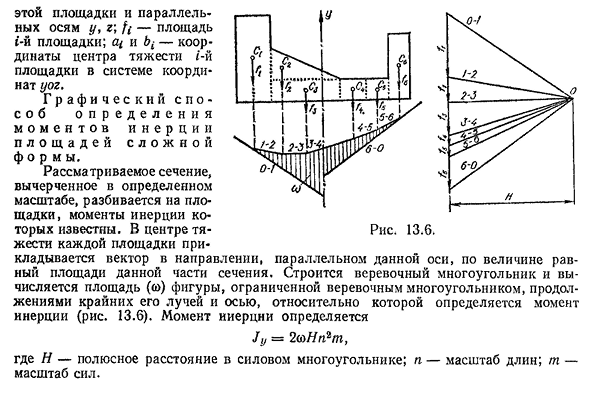
Параллельно осям 250, y и g этого сайта. fi — площадь t-й платформы. Su и являются координатами центра тяжести i-й платформы в системе координат Разочарование Грэмпа Оценить, что это за м. Рассматриваемый раздел выполнен в масштабе и разделен на платформы с известными моментами инерции. Вектор применяется к центроиду каждого узла в направлении, параллельном этой оси, с размером, равным площади этого сечения. Создается канатный многоугольник и вычисляется площадь фигуры, окруженной канатным многоугольником, его экстремальное расширение луча и ось, по которой определяется момент инерции (рис. 13.6). Jу = 2аНп в момент зажигания? Определяется Т. Где Н — полярное расстояние многоугольника силы. n — шкала длины. т шкала силы.
Смотрите также:

