Момент силы относительно центра (точки)
Возникновение понятия момента силы относительно центра связано с задачей о рычаге.
Представим себе твердое тело (рис. 44), имеющее сферическую шарнирную 1) опору, помещенную в центре
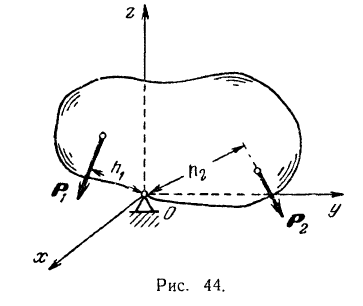
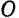тяжести тела. Если к телу приложить силу 
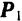на некотором расстоянии 
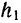от неподвижной точки 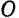, то тело начнет вращаться вокруг этой точки. Если же к телу приложить еще и другую силу 
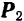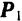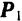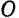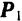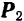(рис. 44), стремящуюся вращать тело в направлении, противоположном вращению силой в плоскости силы и точки , и если при этом отношение модулей сил и будет обратно пропорционально их расстояниям 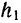и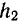 
от неподвижной точки 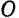, то тело будет оставаться в равновесии.
Вращательное действие силы 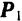будет уравновешиваться вращательным действием силы 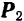, если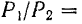 
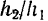и, следовательно, 
.
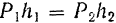Таким образом, мерой вращательного эффекта силы относительно какой-либо точки (центра) является произведение модуля силы на плечо, т. е. на кратчайшее расстояние ее линии действия от центра момента. Это произведение называется модулем момента силы относительно этого центра.
Для эквивалентности вращательного действия двух сил относительно какого-либо центра равенства модулей их моментов относительно этого центра недостаточно. Необходимо еще, чтобы совпадали плоскости, проходящие через линии действия сил и центр моментов, и чтобы силы вращали тело вокруг центра моментов з одном и том же направлении.
Таким образом, для полного определения вращательного эффекта силы относительно какого-либо центра необходимо знать не только модуль момента силы, но и указать плоскость, проходящую через линию действия силы и центр момента, а также сторону вращения в этой плоскости.
Положение плоскости в пространстве определяется, как известно, положением перпендикуляра к этой плоскости.
Из всего сказанного вытекает следующее векторное определение момента силы относительно точки:, моментом силы относительно какой-либо точки 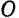(центра) называется приложенный к этой точке вектор, направленный перпендикулярно к плоскости, в которой расположены линия действия силы и центр 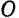, и притом в ту сторону, откуда вращение тела силой представляется совершающимся против часовой стрелки.
Вектор момента силы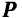 
относительно центра 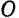будем обозначать символом 
.
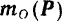Модуль момента силы относительно центра равен, как было сказано выше, произведению модуля силы на ее плечо, т. е. на длину перпендикуляра, опущенного из центра момента на линию действия силы (рис. 45):
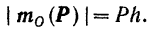
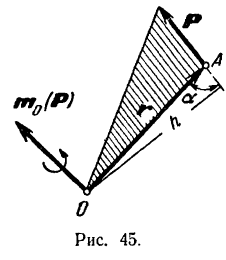
Рассуждая так же, как и при установлении векторного выражения для момента пары, можно сказать, что момент силы относительно какого-либо центра равен векторному произведению радиуса-вектора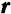 
, проведенного из центра момента в точку приложения силы (рис. 45), на вектор силы
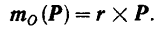
Момент силы относительно точки является одним из важнейших понятий механики. Обобщая это понятие, можно находить момент относительно любой точки, независимо от того, может ли в действительности тело вращаться вокруг этой точки.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
