Момент силы относительно точки
Если к телу приложить силу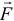 
в точке 
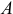(рис. 3.1), оно начнет вращаться вокруг шарнира 
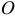. Вращательный эффект будет определяться величиной силы и расстоянием от точки 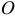до линии действия силы, т.е. произведением
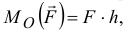
которое называется моментом силы 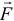относительно точки 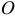, а кратчайшее расстояние 
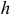. от точки до линии действия силы — плечом силы.
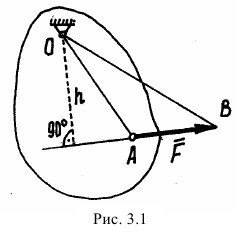
Чтобы момент силы определял не только эффективность вращательного действия, но и направление вращения, условились ставить знак (+) или (-). Если сила стремится повернуть тело против часовой стрелки, (+); если по направлению вращения часовой стрелки, (-).
Если плечо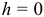 
, то есть линия действия силы проходит через точку 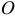, момент силы равен нулю.
Заметим, что площадь треугольник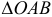а 
равна
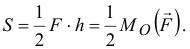
Значит, момент силы относительно точки численно равен двум площадям такого треугольника
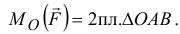
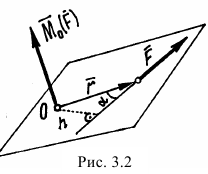
Для того чтобы момент силы определял еще и плоскость, в которой происходит вращение, будем изображать его вектором, направленным перпендикулярно плоскости, в которой расположены точка и сила. И направлять в такую сторону, что если смотреть оттуда, увидим вращение тела вокруг точки против часовой стрелки (рис. 3.2). Нетрудно доказать, что вектор момента силы относительно точки есть векторное произведение радиуса-вектора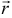 
точки приложения силы на вектор силы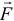
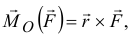
(радиус-вектор 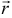— это вектор, проведённый из точки 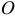и определяющий положение точки, расположенной на его конце).
Действительно, модуль векторного произведения
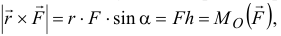
и направлен этот вектор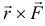 
(по правилу определения направления вектора векторного произведения) так же, как вектор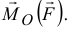 
Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:
Помощь по теоретической механике
Кстати возможно вам будут полезны эти страницы:
