Момент силы относительно оси
Пусть на тело, которое может вращаться вокруг оси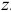 
, действует сила 
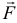(рис. 3.3).
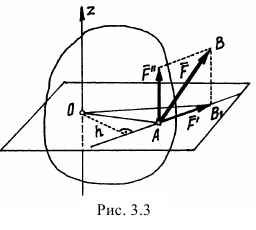
Если через начало вектора силы, точку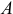 
, провести плоскость, перпендикулярную оси, и разложить силу на две составляющие 
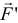и 
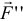, то нетрудно будет заметить, что сила 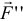, параллельная оси, будет только сдвигать тело вдоль оси. А вращать тело будет лишь сила 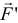расположенная в плоскости. И вращательное действие будет определяться моментом этой силы 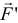относительно точки 
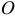, точки пересечения оси с плоскостью. Значит, момент силы 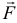относительно оси
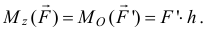
Так как составляющая силы 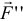при определении момента относительно оси не потребовалась, то правило определения этого момента можно сформулировать так:
Чтобы найти момент силы относительно оси, надо спроектировать вектор силы на плоскость, перпендикулярную оси, и определить момент этой проекции относительно точки пересечения оси с плоскостью.
Заметим, что если вектор силы параллелен оси или линия действия силы пересекает ось, момент силы относительно оси равен нулю. Или иначе, если вектор силы и ось расположены в одной плоскости, момент силы равен нулю.
Чтобы момент силы относительно оси указывал и направление вращения, будем использовать знак (+) или (-).
Если посмотрим на силу со стороны стрелки оси и увидим, что сила стремится вращать тело вокруг оси против часовой стрелки, момент будем считать положительным. Если по часовой — отрицательным.
Обратим внимание на то, что знак момента зависит не только от направления силы, но и от направления оси.
И еще. Из рис.3.3 видно, что площадь треугольник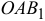а 
равна
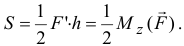
Поэтому момент силы относительно оси равен двум площадям этого треугольника
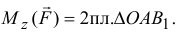
Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:
Помощь по теоретической механике
Кстати возможно вам будут полезны эти страницы:
