Оглавление:
Момент силы относительно оси
Проекция момента силы относительно точки на какую-либо ось, проходящую через эту точку, называется моментом силы относительно соответствующей оси.
Обозначая символом 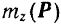 момент силы
момент силы 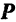 относительно оси
относительно оси 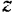 , проходящей через центр
, проходящей через центр 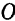 , будем иметь согласно определению:
, будем иметь согласно определению:
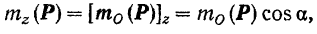
где 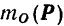 —модуль момента
—модуль момента 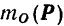 силы относительно точки
силы относительно точки 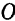 ,
, 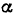 — угол между направлением вектора
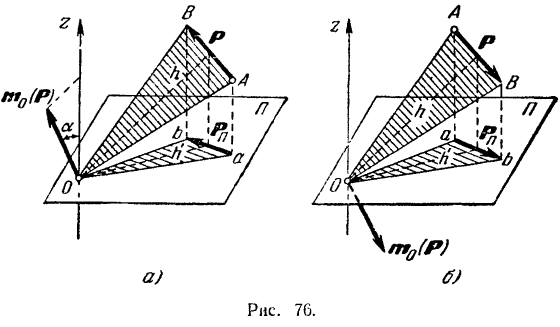
— угол между направлением вектора 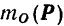 и направлением оси проекций (рис. 76, а).
и направлением оси проекций (рис. 76, а).
Так как всякий свободный вектор вполне определяется своими проекциями па координатные оси, то момент силы относительно какой-либо точки можно определить, найдя моменты данной силы относительно координатных осей, проходящих через эту точку.
Теорема. Момент силы относительно оси равен, алгебраической величине момента проекции этой силы на плоскость, перпендикулярную к оси. относительно точки пересечения оси с этой плоскостью.
Спроектируем силу 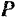 на плоскость
на плоскость 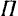 , перпендикулярную к оси
, перпендикулярную к оси 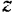 (рис. 70, а), и найдем момент проекции
(рис. 70, а), и найдем момент проекции 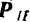 силы
силы 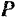 на плоскость
на плоскость 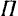 относительно точки
относительно точки 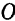 пересечения оси
пересечения оси 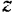 с этой плоскостью
с этой плоскостью
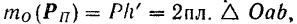
где площадь 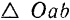 является проекцией на плоскость
является проекцией на плоскость 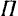 площади
площади 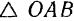 .
.
Площадь проекции плоской фигуры равна площади проектируемой фигуры, умноженной на косинус угла между плоскостью проектируемой фигуры и плоскостью проекции. Угол между плоскостями измеряется углом между перпендикулярами к этим плоскостям. Так как перпендикуляром к плоскости 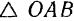 является вектор
является вектор 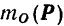 , а перпендикуляром к плоскости
, а перпендикуляром к плоскости 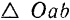 — ось
— ось 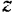 , то угол между этими плоскостями равен
, то угол между этими плоскостями равен 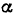 (рис. 76, а). Следовательно,
(рис. 76, а). Следовательно,
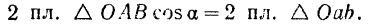
Модуль момента силы 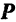 относительно точки
относительно точки 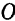 равен
равен
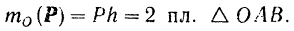
Таким образом получаем, что
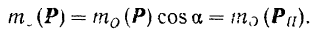
Если направление силы изменить на противоположное, то и вектор 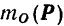 изменит свое направление на противоположное. В этом случае (рис. 76, б) угол между направлением вектора
изменит свое направление на противоположное. В этом случае (рис. 76, б) угол между направлением вектора 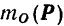 и положительным направлением оси
и положительным направлением оси 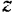 будет тупым и проекция этого век-юра на ось
будет тупым и проекция этого век-юра на ось 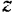 будет отрицательной. Но так как при этом вращение вектора
будет отрицательной. Но так как при этом вращение вектора 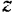 вокруг точки
вокруг точки 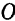 будет направлено по ходу стрелки часов (если смотреть с положительного конца оси
будет направлено по ходу стрелки часов (если смотреть с положительного конца оси 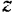 ), то
), то 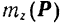 будет также отрицательным. Итак,
будет также отрицательным. Итак,
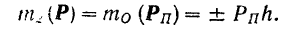
Тот или другой знак в формуле (34) определяется по следующему правилу: если для наблюдателя, смотрящего на плоскость с положительной стороны оси 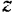 , проекция силы
, проекция силы 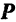 на плоскость
на плоскость 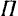 представляется вращающей тело вокруг оси
представляется вращающей тело вокруг оси 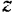 против хода стрелки часов, то момент считается положительным-, в противном случае его считают отрицательным.
против хода стрелки часов, то момент считается положительным-, в противном случае его считают отрицательным.
Момент силы относительно оси является, очевидно, скалярной величиной.
Для того чтобы уяснить физический смысл понятия момента силы относительно оси, рассмотрим такой пример.
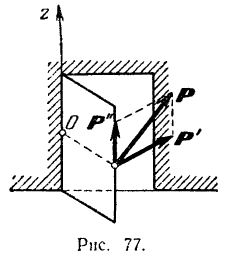
Пусть сила 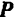 , приложенная к телу, которое может вращаться вокруг неподвижной оси, например, к двери, вращающейся на петлях вокруг оси
, приложенная к телу, которое может вращаться вокруг неподвижной оси, например, к двери, вращающейся на петлях вокруг оси 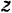 (рис. 77), не лежит на плоскости, перпендикулярной к этой оси.
(рис. 77), не лежит на плоскости, перпендикулярной к этой оси.
Разложим силу 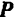 на две составляющие:
на две составляющие: 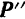 , параллельную оси вращения тела, и
, параллельную оси вращения тела, и 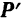 , лежащую в плоскости, перпендикулярной к этой осн. Ясно, что составляющая
, лежащую в плоскости, перпендикулярной к этой осн. Ясно, что составляющая 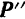 не может вращать тело: она может лишь только перемещать его вдоль оси (снять дверь с петель). Вращательное движение телу может сообщать лишь составляющая
не может вращать тело: она может лишь только перемещать его вдоль оси (снять дверь с петель). Вращательное движение телу может сообщать лишь составляющая 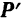 . Таким образом, вращательный эффект силы
. Таким образом, вращательный эффект силы 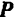 относительно оси определяется вращательным эффектом ее составляющей
относительно оси определяется вращательным эффектом ее составляющей 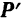 , являющейся проекцией силы
, являющейся проекцией силы 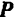 на плоскость, перпендикулярную к оси. Последний же зависит от модуля составляющей
на плоскость, перпендикулярную к оси. Последний же зависит от модуля составляющей 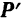 и от ее расстояния до оси, т. е. определяется моментом составляющей
и от ее расстояния до оси, т. е. определяется моментом составляющей 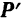 относительно точки пересечения оси с плоскостью, в которой расположена эта сила.
относительно точки пересечения оси с плоскостью, в которой расположена эта сила.
Понятие о моменте силы относительно оси является одним из важнейших понятий механики. Обобщая его, можно находить момент силы относительно любой оси, независимо от того, может ли в действительности тело вращаться вокруг этой оси.
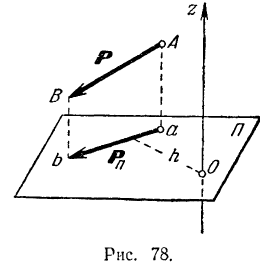
Для того чтобы определить момент какой-либо силы 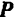 относительно какой-либо оси
относительно какой-либо оси 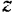 (рис. 78), нужно провести любую плоскость
(рис. 78), нужно провести любую плоскость 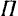 , перпендикулярную к данной оси, и спроектировав силу на эту плоскость, найти алгебраическую величину момента этой проекции силы относительно точки пересечения оси с плоскостью
, перпендикулярную к данной оси, и спроектировав силу на эту плоскость, найти алгебраическую величину момента этой проекции силы относительно точки пересечения оси с плоскостью 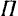 .
.
Установленный ранее (§ 21) для плоской системы сил алгебраический момент силы относительно точки можно, очевидно, рассматривать как момент силы относительно оси, проходящей через центр момента перпендикулярно к плоскости, в которой лежат эта точка и сила.
Заметим, что:
1) момент силы относительно данной оси не изменяется при перенесении силы вдоль ее линии действия, так как при этом не изменяется ни проекция силы на данную плоскость, ни ее плечо;
2) момент силы относительно оси равен нулю в тех случаях, когда линия действия силы и ось лежат в одной плоскости.
При этом возможны два случая.
а) Сила параллельна оси. В этом случае равна нулю проекция силы на плоскость, перпендикулярную к оси.
б) Линия действия силы пересекает ось. В этом случае проекция силы на плоскость проходит через точку
пересечения оси с плоскостью, и ее плечо относительно этой точки равно нулю.
Пример задачи:
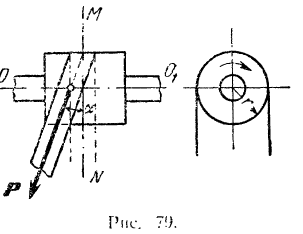
Сбегающая ветвь ремня, действующая на окружности шкива радиусом 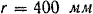 , с силой
, с силой 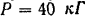 отклонена от средней плоскости шкива
отклонена от средней плоскости шкива 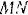 на угол
на угол 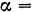
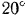 . Определить момент силы относительно оси
. Определить момент силы относительно оси 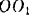 i вала (рис. 79).
i вала (рис. 79).
Решение:
Спроектируем силу 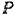 на плоскость
на плоскость 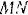 , перпендикулярную к оси вала. Модуль этой проекции
, перпендикулярную к оси вала. Модуль этой проекции 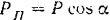 . Расстояние ее до точки пересечения оси с плоскостью
. Расстояние ее до точки пересечения оси с плоскостью 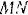 (т. е. до центра шкива) равно
(т. е. до центра шкива) равно  . Таким образом, модуль момента
. Таким образом, модуль момента
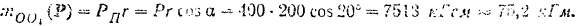
Если бы средняя линия рассматриваемой части ремня совпадала со средней плоскостью шкива, то момент той же силы относительно оси вала равнялся бы
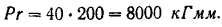
Пример задачи:
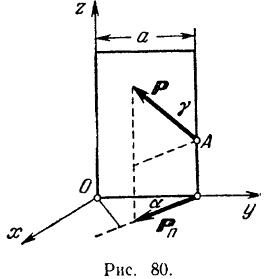
К двери, вращающейся около вертикальной оси 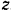 , в точке
, в точке 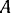 приложена сила
приложена сила 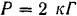 под углом
под углом 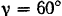 к вертикали; вертикальная плоскость, в которой лежит эта сила, образует с плоскостью двери угол
к вертикали; вертикальная плоскость, в которой лежит эта сила, образует с плоскостью двери угол 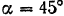 (рис. 80). Определить момент силы
(рис. 80). Определить момент силы 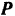 относительно оси
относительно оси 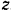 , если ширина двери
, если ширина двери 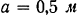 .
.
Решение:
Проведем плоскость 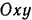 , перпендикулярную к оси
, перпендикулярную к оси 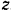 и спроектируем силу
и спроектируем силу 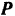 из эту плоскость; модуль этой проекции
из эту плоскость; модуль этой проекции 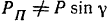 . Из точки
. Из точки 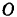 пересечения оси с плоскостью опускаем перпендикуляр на линию проекции; длина этого перпендикуляра
пересечения оси с плоскостью опускаем перпендикуляр на линию проекции; длина этого перпендикуляра 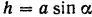 . Таким образом,
. Таким образом,
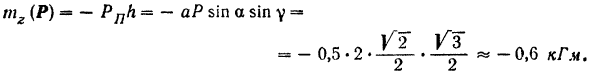
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:

