Момент пары как вектор
Было доказано, что пару, не изменяя ее действия на абсолютно твердое тело, можно переносить не только в любое положение в плоскости действия пары, но и в любую другую параллельную плоскость. Неизменным во всех случаях должны оставаться лишь модуль момента нары и направление ее вращения в соответствующей плоскости.
Так как положение всех параллельных плоскостей в пространстве вполне определяется положением перпендикуляра к любой из них, то для определения действия пары, входящей в состав сил, произвольно расположенных в пространстве, достаточно знать три фактора: 1) положение перпендикуляра к плоскости действия нары, 2) направление вращения нары в ее плоскости и 3) модуль момента нары.
По аналогии с вектором силы, также отражающим три ее фактора (линию действия, направление и модуль силы), можно сказать, что момент пары является вектором. Момент нары, направлен по перпендикуляру к плоскости действия пары в ту сторону, откуда вращение тела парой представляется происходящим против направления вращения стрелки часов. Модуль момента пары равен произведению модуля силы пары на ее плечо.
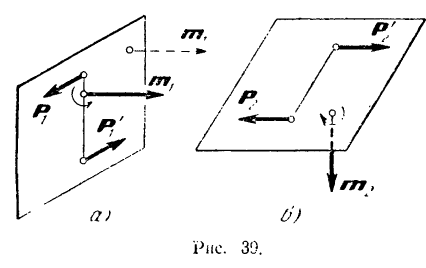
Изображенные на рис. 39, а и 39,6 векторы 
и 
представляют собой соответственно моменты пар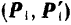 
и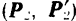 
.
Так как пару можно переносить в ее плоскости как угодно, то ее момент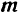 
не имеет определенной линии действия и является свободным вектором. Такие векторы можно переносить параллельно самим себе в любую точку. На рис. 39, а пунктиром показано другое положение момента 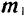пары .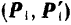
Свободные векторы называются, как известно, равными, если они имеют одинаковые модули, параллельны и направлены в одну и ту же сторону. Отсюда следует условие эквивалентности нар, выраженное в общей форме: пары эквивалентны, если их моменты равны между собой.
Вспоминая понятия векторной алгебры, можно сказать, что момент пары равен векторному произведению вектора, проведенного из точки приложения одной силы пары в точку приложения второй, на вторую силу (рис. 41):
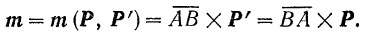
В самом деле, секторным произведением двух векторов называется вектор, который определяется следующими признаками:
1) Модуль этого сектора равен произведению модулей перемножаемых секторов на синус угла между ними. Следовательно, модуль векторного произведение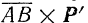 
(рис. 41) равен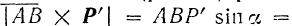 
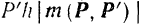, т. е. равен модулю момента пары.
2) Направлен этот вектор должен быть перпендикулярно к плоскости, проходящей через перемножаемые векторы, и в ту сторону, откуда кратчайший поворот первого сомножителя (в данном случае вектора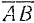 
) до совмещения со вторым сомножителем (в данном случае с вектором 
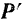), если перенести начала обоих секторов в общую точку, был бы виден происходящим против хода стрелки часов. Таким образом, вектор 
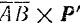направлен так же, как и вектор 
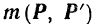, и равен ему по модулю.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
| Пара сил |
| Теоремы об эквивалентности пар |
| Сложение пар. Условие равновесия системы пар + пример решения |
| Момент силы относительно центра (точки) |
