Момент пары и момент силы относительно точки как алгебраические величины
В общем случае, когда силы, действующие на тело, расположены как угодно в пространстве, моменты пар и моменты сил относительно точки рассматриваются как векторы, перпендикулярные к плоскости действия соответствующих пар или к плоскости, в которой лежит линия действия соответствующей силы и центр моментов. Для плоской же системы сил, т. е. для случая, когда линии действия всех сил, приложенных к телу, лежат в одной плоскости, моменты пар и моменты сил относительно точки, лежащей в той же плоскости, будут перпендикулярны к этой плоскости и, следовательно, параллельны между собой. Модуль результирующего момента будет равен абсолютному значению алгебраической суммы составляющих моментов, если считать моменты, вращающие тело в одну сторону, положительными, а в противоположную сторону— отрицательными. Направлен же результирующий вектор будет всегда перпендикулярно к плоскости, в которой расположена данная система сил, в сторону, определяемую знаком алгебраической суммы.
Таким образом, для плоской системы сил отпадает необходимость в векторном представлении момента пары и момента силы относительно точки, и мы можем рассматривать их как скалярные алгебраические величины, вполне определяемые их модулем и знаком.
Алгебраической величиной момента пары называется взятый со знаком плюс или минус модуль момента пары, т. е. произведение модуля силы пары на ее плечо
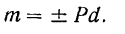
При этом момент пары считается положительным, если пара стремится вращать тело в направлении, противоположном ходу стрелки часов, и отрицательным — если пира стремится повернуть тело по ходу стрелки часов.
Если на тело действуют несколько пар, расположенных в одной или в параллельных плоскостях, то, как это следует из сказанного выше и доказанных ранее (§§16 и 18) теорем об эквивалентности и сложении пар, их можно заменить одной результирующей парой, момент которой равен сумме алгебраических величин моментов составляющих пар. Знак этой суммы определяет сторону, в какую направлено вращение результирующей пары.
Очевидно, что для равновесия системы пар, расположенных в одной или параллельных плоскостях, необходимо и достаточно, чтобы равнялась нулю сумма алгебраических величин моментов составляющих пар.
Для эквивалентности же пар, лежащих в одной или параллельных плоскостях, достаточно только, чтобы они имели одинаковое направление вращения и одинаковый по модулю момент. Поэтому в задачах плоской статики на схемах пару часто изображают круговой стрелкой (рис. 49), показывающей направление вращения пары, и рядом пишут модуль момента.
Алгебраической величиной момента силы относительно какой-либо точки называется взятое со знаком плюс или минус произведение модуля силы на ее плечо, т. е. на длину перпендикуляра, опущенного из этой точки на линию действия силы:
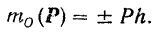
Тот или другой знак в этой формуле берется по правилу, аналогичному правилу знаков для момента пары: если сила стремится повернуть тело вокруг центра моментов против хода стрелки часов, момент считается положительным, если по ходу стрелки часов — отрицательным. Так, например, для силы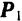 
на рис. 50 будем иметь:
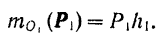
Для силы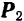 
имеем:
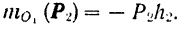
Нужно отметить, что момент одной и той же силы может иметь и положительное и отрицательное значение, в зависимости от взаимного расположения силы и центра моментов, т. е. той точки, относительно которой берется момент. Так, например (рис. 50), момент силы 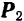относительно точки 
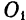равен 
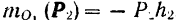, а момент той же силы относительно точки 
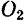равен то, 
.
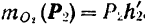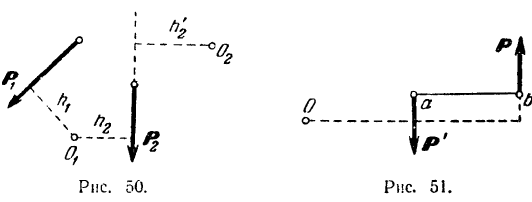
В дополнение к изложенной ранее (глава IV) теории пар, докажем еще одну теорему, которой удобно пользоваться при решении ряда задач.
Теорема. Момент пары равен сумме алгебраических величин моментов сил, составляющих пару, относительно любой точки, лежащей в плоскости действия данной пары.
Доказательство. Пусть мы имеем пару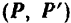 
с плечом 
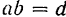(рис. 51). Момент этой пары 
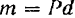. Взяв за центр моментов произвольную точку 
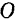, лежащую в плоскости действия данной пары, будем иметь: 
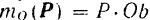и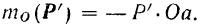 
. Складывая эти равенства и принимая во внимание, что
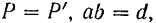
получим:
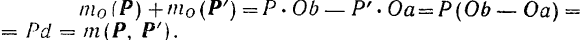
Сумма моментов сил пары не зависит, следовательно, от выбора центра моментов. Она равна постоянной для данной пары величине — моменту этой пары, характеризующему вращательное действие пары на тело.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
