Момент инерции тела относительно оси
Движение системы зависит не только от действующих на нее сил и массы системы, но еще и от распределения этой массы. Помимо положения центра масс системы, распределение ее массы характеризуется еще одной, имеющей очень важное значение в динамике системы, величиной — моментом инерции.
Моментом инерции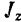 
твердого тела относительно какой-либо оси 
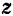(осевым моментом инерции) называется скалярная величина, равная сумме, составленной из произведений массы 
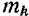каждой точки тела на квадрат ее расстояния 
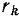до данной оси.
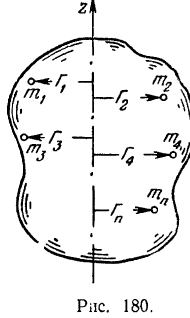
Для того чтобы найти момент инерции твердого тела относительно какой-либо его оси 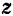(рис. 180), необходимо разбить все тело на очень большое число 
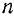элементарных объемов, составить сумму из произведений массы каждого элементарного объема тела на квадрат его расстояния до данной оси и затем вычислить предел этой суммы, предполагая, что число 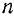стремится к бесконечности, а масса каждого элемента объема стремится к нулю:
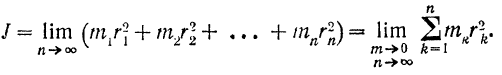
Для краткости символы предела и пределы суммирования будем опускать и момент инерции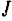 
тела относительно какой-либо оси определять просто как сумму, составленную из произведений массы 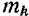каждой частицы тела на квадрат расстояния этой частицы от данной оси:
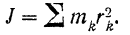
При приближенном вычислении моментов инерции полых цилиндрических тел с тонким ободом (например, маховых колес) иногда пренебрегают толщиной обода и принимают такое тело за бесконечно тонкое кольцо (материальную окружность). В этом случае можно считать все точки тела находящимися на одинаковом расстоянии от оси 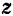его вращения. Полагая в формуле (139) 
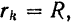, будем иметь:
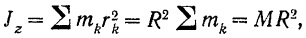
Момент инерции бесконечно тонкого кольца (материальной окружности) относительно его оси вращения равен произведению его массы на квадрат радиуса:
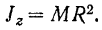
Иногда бывает удобно момент инерции 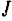тела относительно оси представить в виде произведения массы 
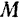тела на квадрат длины некоторого отрезка 
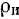называемого радиусом инерции тела относительно соответствующей оси:
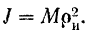
Очевидно, что под радиусом инерции тела относительно какой-либо оси можно понимать радиус такого бесконечно тонкого кольца, в котором нужно сосредоточить всю массу 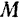тела, чтобы получить момент инерции кольца, равный моменту инерции тела относительно этой оси.
Если момент инерции тела относительно оси найден, то радиус инерции тела относительно этой оси легко находится из предыдущей формулы:
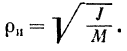
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
