Оглавление:


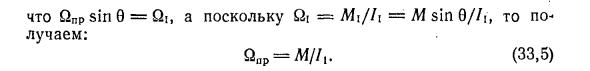

Момент импульса твердого тела
- Момент импульса твердого тела. Как известно, величина момента импульса системы составляет Из выбора определенных точек. В механике твердого тела наиболее разумным выбором для этой точки является начало движущейся системы координат.
Центр инерции тела. Далее М понимает моменты, определенные таким образом. Согласно уравнению (9.6) Центр инерции тела, его момент М, совпадает с «уникальным моментом», который относится только к движению точки тела относительно центра инерции.
ориентированы вдоль главной оси инерции Тело Людмила Фирмаль
Другими словами, по определению M = mn mn [rv] Вы должны заменить v на [Пη . M = 5 ^ m [r [ftr]] = 12m {r2Q-r (rft)}, Или в тензорной записи: Mi = ^ 2m {xiQi-XiXkttk} = -XiXk}. Наконец, учитывая определение тензора инерции (32.2), мы, наконец, получаем Mi = Iiknk. (33,1) Когда оси Ж1, Ж2, х% , эта формула обеспечивает: Mi = iifii, M2 = / 2 ^ 2, Ms = / 3 ^ 3- (33,2) Особенно для мяча, когда все три основных
Когда моменты инерции совпадают, это просто становится: М = / фут, (33,3) Другими словами, вектор момента пропорционален вектору угловой скорости и имеет то же направление. Общий случай любого объекта, обычно вектор M То есть M и ft находятся в одном и том же направлении, только если направление не соответствует вектору ft и тело вращается вокруг одной из главных осей инерции.
- Рассмотрим твердое свободное движение, на которое не влияют внешние силы. Предположим, что равномерное поступательное движение интереса исключено. Поэтому поговорим о свободном вращении тела.
Подобно закрытой системе, момент импульса свободно вращающегося объекта постоянен. Для шарового верха M = const просто становится ft = const. Это общее Когда верхняя часть шара вращается свободно, это простое вращение вокруг определенной оси.
свободное вращение ротора представляет собой равномерное вращение вокруг направления Людмила Фирмаль
Корпус ротатора такой же простой. Опять М = / фут, Вектор ft перпендикулярен оси ротора. Таким образом, , перпендикулярного этой плоскости в одной плоскости. Закон сохранения моментов достаточно для определения Более сложное свободное вращение симметричного волчка.
Выберите ось x2 перпендикулярно, используя случайность, чтобы выбрать направление главных осей инерции x1, x2 (перпендикулярно оси симметрии вершины x3) Плоскость, определяемая постоянным вектором М и мгновенным положением оси G3. Затем M2 = 0 и {} 2 = 0 из уравнения (33.2).
Это направление М, фут и Верхняя ось каждого момента находится в одной плоскости (рис. 46). Однако это, в свою очередь, означает, что скорость v = [ftr] всех точек на верхней оси в каждый момент времени перпендикулярна указанной плоскости.
Другими словами, ось вершины (см. Ниже) вращается равномерно вокруг оси М, представляющей конус (так называемая нормальная прецессия вершины). Одновременно с прецессией сама вершина вращается равномерно вокруг оси.
Угловые скорости для обоих этих вращений могут быть выражены просто как: Вырезать указанное значение момента М и угла наклона 0 верхней оси По направлению М. Угловая скорость верхнего вращения вокруг оси — это просто проекция вектора Q на эту ось. — ~ T — cos0. (33,4)
Для определения скорости прецессии Γ ^ Pr вектор Q необходимо разложить на вдоль х и м. Из них первый не вызывает смещения оси самой вершины, поэтому второй дает желаемую угловую скорость прецессии. 46 Это ясно из структуры рисунка Поскольку f ^ np sin 0 = fii и fix = M \ / I \ = M sin 0 / ii, = M / 1 . (33,5)
Смотрите также:
| Угловая скорость в физике | Уравнения движения твердого тела |
| Тензор инерции в физике | Эйлеровы углы в физике |
Если вам потребуется помощь по физике вы всегда можете написать мне в whatsapp.

