Модуль действительного числа, его график и свойства

Понятие модуля действительного числа, его график и свойства

Абсолютной величиной (модулем) действительного числа x называется само это число, если x — положительно; нуль, если x равен нулю; число, противоположное числу x , если x — отрицательно.

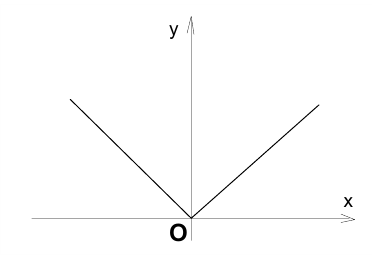
Модуль действительного числа x обозначается |х|. Функция у =|х|

относится к алгебраическим, так как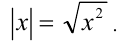

Итак, по определению, имеем: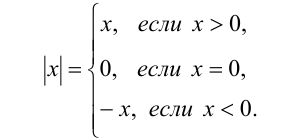

Аналогично водится понятие модуля для произвольного выражения:

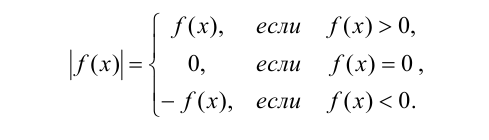
Основные свойства модуля

Пусть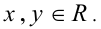

Тогда справедливы следующие свойства:

1. Модуль числа неотрицателен:
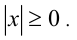
2. Модуль числа не меньше самого числа: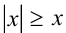, причём неравенство обращается в равенство тогда и только тогда, когда 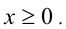Модуль числа не меньше того же числа, взятого со знаком минус: 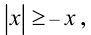причём неравенство обращается в равенство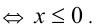
3. Модули противоположных чисел равны:
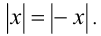
4. Квадраты числа и его модуля равны:
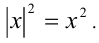
5. Арифметический корень чётной степени, извлечённый из такой же степени числа, равен модулю числа:
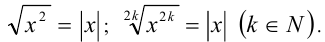
6. Модуль произведения двух чисел равен произведению их модулей:
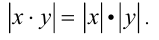
7. Модуль частного равен частному модулей:
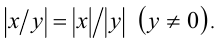
8. Модуль суммы двух чисел не превышает суммы их модулей:

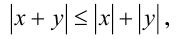
причём неравенство обращается в равенство тогда и только тогда, когда числа имеют одинаковые знаки либо хотя бы одно из них обращается в нуль (т.е. когда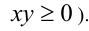

Модуль разности двух чисел также не превосходит суммы их модулей: 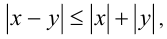причём равенство имеет место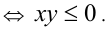

Доказательство. Пользуясь тем, что обе части неравенства 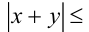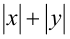неотрицательны, возведём его в квадрат и получим равносильное неравенство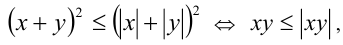которое, очевидно, верно при всех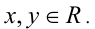

Следовательно, исходное неравенство также верно. При этом доказываемое неравенство обращается в равенство одновременно с неравенством 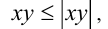т.е. когда 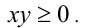Для доказательства свойства 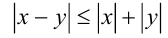достаточно подставить в неравенство 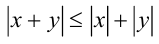вместо у выражение (-y).

Приведём здесь также известное обобщение этого неравенства на случай произвольного количества чисел: если 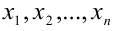— любые действительные числа, то

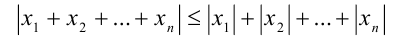
(неравенство доказывается методом математической индукции).

Модуль суммы (разности) двух чисел не меньше модуля разности их модулей:

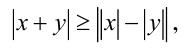
причём неравенство обращается в равенство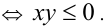

А также 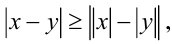причём неравенство обращается в равенство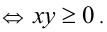

Доказательство. Пользуясь тем, что обе части неравенства 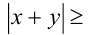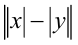неотрицательны, возведём его в квадрат и получим равносильное неравенство

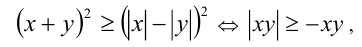
которое, очевидно, выполняется при всех 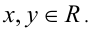При этом исходное неравенство обращается в равенство одновременно с неравенством 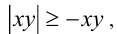т.е. когда 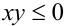(числа x, у имеют разные знаки или хотя бы одно из них обращается в нуль). Для доказательства свойства 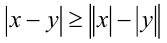достаточно подставить в доказанное неравенство 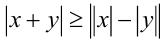вместо у выражение (-y) .

10.Действительное число всегда представимо в виде произведения его модуля на функцию его знака: 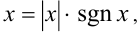где

есть известная в математике функция, называемая «сигнум», или «знак числа».

Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:

Предмет математика

Эти страницы возможно вам будут полезны:

Замена переменных: рационализирующие подстановки в математике с примерами решения

Решение задачи на отдельных промежутках ОДЗ

Методы решения задач с модулями в математике

Раскрытие модулей но определению в математике с примерами решения