Оглавление:


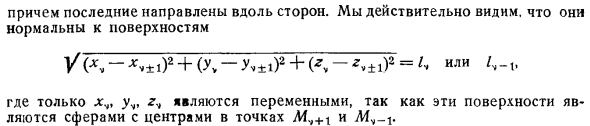

Множители Лагранжа
- Смещение точки M связано отношением h. соотношение h получается путем дифференцирования уравнения 1. Эти отношения h между вариациями координат Zl указывают на то, что k из этих вариаций могут быть выбраны произвольно. Эти вариации называются независимыми вариациями, а остальные определяются равенствами 3 зависимыми вариациями. Чтобы найти условие равновесия, мы применяем метод множителя Лагранжа. Уравнение 3 для неопределенных факторов Xj, Xg соответственно… Умножьте Chl и добавьте его к выражению 2. Затем определите коэффициент так, чтобы коэффициент был равен нулю для H зависимых колебаний величины результата. Тогда коэффициент независимых колебаний должен также disappear.
Эти два свойства могут рассматриваться как следствия аналогичных свойств, полученных для веревочного многоугольника. Людмила Фирмаль
В результате нам нужно определить X таким образом, чтобы все коэффициенты исчезли, и мы получим соединение Zl 4 Уравнение Эти уравнения вместе с уравнением H 1 ограничения образуют полную систему уравнений Zn + L, которые определяют координаты Zn и вспомогательные неизвестные H X. Это уравнения общего равновесия. Как только коэффициент K установлен, реакция связи может быть determined. In фактически, мы можем видеть, что если отбросить связь = 0 и добавить силу проекции X, y к данной силе, действующей на точку, уравнение равновесия не изменится.
- Эта сила действие Связь с точкой, то есть реакция общения. У нас есть d , величина этой силы имеет прямое отношение. Его направление, Д Т Л jy, перпендикулярно поверхности, оказывается assumed. In уравнение,= 0, x., все координаты кроме 2n задаются числом, соответствующим положению равновесия, координаты xv, yv, r являются текущими. Образцы. Примените предыдущий вывод к равновесию канатного многоугольника с n сторонами, ребра которого зафиксированы в 2 заданных точках. То есть существует n уравнений связи. Г х х.+ 1 2 4 г, г.+ 1 П4 р г н З. = О в = 0, 1, 2,…
Далее необходимо будет исследовать эту систему, которая может допускать одно, два и даже бесчисленное множество решений. Людмила Фирмаль
Координаты x0, y0 и веса равны Z0 и xn, yn и zn указаны. Общее уравнение 4 х. Т К, 4 Х. 4 х. Четыре Г Е. 1 к г г 1. Х 1 Лм 4 х. г л Ноль 0. 0. Если мы выразим, что сила F уравновешена с напряжением 2 нитей, заканчивающихся в точке I, то они фактически совпадут с той, которая получена с использованием основного method. In абсолютное значение натяжения, последнее направлено вдоль сторон. Вы действительно можете видеть, что он перпендикулярен поверхности. В л. х ТИ 2 + г, г 1 2 + Л В2 = Z или Здесь переменными являются только y,,, r.
Смотрите также:
Решение задач по теоретической механике
| Приложения. Тяжелые системы | Приложение принципа возможных скоростей к равновесию нитей |
| Принцип Торричелли | Общие теоремы, выводимые из принципа возможных скоростей |

