Оглавление:

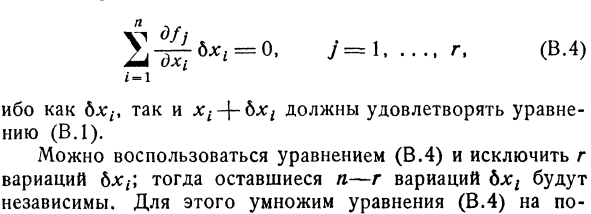





Множители Лагранжа
- Множитель Лагранжа Во многих задачах физики, если x-t не является независимым, но должен удовлетворять определенному числу, например r дополнительных условий, n переменных F(xv xv …. необходимо найти экстремумы функции (xn). фдж(в XV Х2,хп)= CJt J = 1,то р, (Б. 1.) СУ-это константа. Обратите внимание, что изменение F должно быть равно нулю, когда xt изменяется с xt на xi — \ — bxi, чтобы найти значение xit, которое достигает экстремума. н. (В. З.)
Но xt не является независимым, а должен удовлетворять уравнению н. (V. Два) Равенство (B. 2) отбрасывает все термины для bl /за исключением 1-го термина. Если дополнительных условий нет, а bxt является независимой вариацией, то уравнение(B. 2)будет известным условием экстремальных значений. я = 1 6n;, -, xi — * — в обоих случаях bxl-формула (B. 1) должна соответствовать. Формула (B. 4)
Постоянные коэффициенты I (необходимо определить) и их формулы(Б. 2) дополняют. Людмила Фирмаль
Вы можете исключить колебание R 6lu используя. Тогда оставшиеся n-r вариации bl ^будут independent. To сделайте это, используя уравнение (B. 4) умножьте Тогда мы получаем — +Г Я ^ л ДХ; + 2Д Ки-генератора типа J-1 (B. 5.) = 0. / −1 Здесь мы находим константу XJt, которая является неопределенным Лагранжем multiplier. It необходимо, чтобы коэффициент переменной xi% составлял xv x2. xg, формула (B. 5) исчезла.
- Это приводит к уравнению ДФ, в <л dfj dхij / = я….. р>(б-6а> и-И. И уравнение (B. 5) сделать Два = / ■ + 1 л (B. 7.) = 0. потому что n — это входная вариация R Уравнения (Б. 7), подставляя в, становятся независимыми, и их коэффициенты должны исчезнуть. В. Л. д / Дж я = р + я….. С. С.(ВББ) J-1 для. Уравнение(В. 6а) и(Б. ВВ можно определить значение n:/, где, при дополнительных условиях, экстремум функции Z7 резца достигается. эти значения x-t по-прежнему являются функциями Xj, но вы можете использовать формулу (B. 1) для удаления Xj. Во многих случаях фактору Xj можно дать простую физическую интерпретацию (см. пример ниже).
Метод неопределенного множителя был разработан La Grunge в 1788 году. Пример. Рассмотрим чистое вещество, которое находится в верхней 1-3 из 3 фаз shown. It необходимо находиться в состоянии равновесия. В. Л. д / Дж я = р + я….. С. С.(ВББ) J-1 для. Уравнение(В. 6а) и(Б. ВВ можно определить значение n:/, где, при дополнительных условиях, экстремум функции Z7 резца достигается. эти значения x-t по-прежнему являются функциями Xj, но вы можете использовать формулу (B. 1) для удаления Xj.
Во многих случаях фактору Xj можно дать простую физическую интерпретацию (см. пример ниже).Метод неопределенного множителя был разработан La Grunge в 1788 году. Пример. Рассмотрим чистое вещество, которое находится в верхней 1-3 из 3 фаз shown. It необходимо находиться в состоянии равновесия.
Во-первых, мы можем видеть, что| x <1> ===(ll <2> =то есть химический потенциал постоянен во всей системе, и множитель Лагранжа в этом случае равен химическому потенциалу. Людмила Фирмаль
Смотрите также:
| А. Некоторые физические константы | Преобразования Лежандра |
| Б. Критическое состояния | Якобианы |

