Оглавление:






Множественная регрессия в нелинейных моделях
- Множественная регрессия с нелинейной моделью Глава 4 показала, что модели линейной регрессии можно объяснить. Они линейны двумя способами: выравнивание переменных и метод Линейный параметр. Для линейного регрессионного анализа Линейность только для параметров из-за переменной нелинейности Его можно удалить, изменив определение.
- Как пример Показать зависимости y = a + $ {x} + $ 2Jx ~ ^ + … (4.5) Его можно переписать в форму, в которой переменная является линейной. j> = a + p, * i + P2 * 2 + -. (4.6) По простому определению z \ = xf, zi = V * 2 и m -> — в случае случайных членов (Явно показано в уравнении) удовлетворяет следующему условию Гаусса-Маркова Заполните его исходными уравнениями, переписанными уравнениями.
Так, например, вы можете оценить вторичные зависимости Значение: y = a + p, x + Pj X2 + u, (5.23) Напишите z = x2 и оцените регрессию между ;; и xnz. Людмила Фирмаль
Для х в принципе коэффициенты полинома можно оценить Необходимый бог. 141 Нелинейность параметров является более серьезной проблемой. если Тем не менее, правая часть модели состоит из отображенного члена или eP * 9, умноженного на Если вы являетесь друзьями, и случайный термин является мультипликативным, модель Линеаризуется по логарифму обеих частей.
Пример: функция спроса у = уфипыв, (5.24) Где у — стоимость продукта, х — доход, р — относительная цена, а v — случай Термины могут быть преобразованы в линейные формы По параметру: log y = log a + p log x + y log p + log v (5.25) Если вы оцениваете регрессию между данными log y, log x и log p, Коэффициент log x является прямой оценкой p-эластичности Спрос по выручке, коэффициент при log p является оценкой у-эластичности Ценовой спрос.
Пример 1. Функция спроса Логарифмическая регрессия между ценами на продукты питания и расходными материалами Личный доход в США оценивался на основе тех же данных, которые использовались Используется в формуле (5.3) для получения следующего результата (в скобках) Указана стандартная ошибка): log y = 2,82 + 0,64 log x-0,48 log p \ R2 = 0,99; (5,26) (0,42) (0,03) (0,12) F = 820,1. Уравнение регрессии показывает эластичность спроса по структуре доходов. 0,64, эластичность спроса по цене составляет 0,48, оба коэффициента значимы Они отличаются от нуля на уровне значимости 1%.
Пример 2. Производственная функция Кобба — Дуглас В 1927 году подготовил экономиста Пола Дугласа Поместите логарифм фактического индикатора на том же графике Выход (Y), стоимость капитала (K) и стоимость рабочей силы (L), затем расстояние От точки графика индикатора выхода до точки графика индикатора стоимости Труд и капитал имеют определенное соотношение.
Затем он нарисовал Попросив математика Чарльза Кобба найти математические зависимости Бридж с этой функцией, и Кобб предложил следующее Особенности: Y = AK * D ~ *. (5,27) Эта функция была предложена Филиппом Виком около 30 лет назад. Вместо (Wicksteed), C. Кобб и П. Дуглас Классик Работа (Кобб, Дуглас, 1929), но они использовали в первую очередь Эмпирические данные приведены в таблице для его построения.
5.1. автор Они не объясняют, как они на самом деле подобрали функцию, 142 Возможно, они использовали начальную форму регрессии Лизу назвали «теорией наименьших квадратов». По их оценке ке, а = V4- Невозможно повторить расчет с использованием регрессионного анализа. Быстрая линеаризация путем логарифмизации обеих частей уравнения Формула. Тогда вы получите две разные оценки.
- Коэффициент log # указывает одну оценку и коэффициент log L, который является оценкой. (1-а), другая оценка может быть рассчитана. Вместо этого, разделить Перепишите функцию с обеих сторон уравнения с помощью L и Как только: Y / L = A (K / L) * v (5,28) (Включая случайный член v). Эта форма может интерпретировать функцию Van как отношение объема производства на одного работника к капитальным затратам Для каждого сотрудника линеаризуйте, взяв логарифм Us: Log (Y / L) = Log A + Log (K / L) + Log v. (5,29)
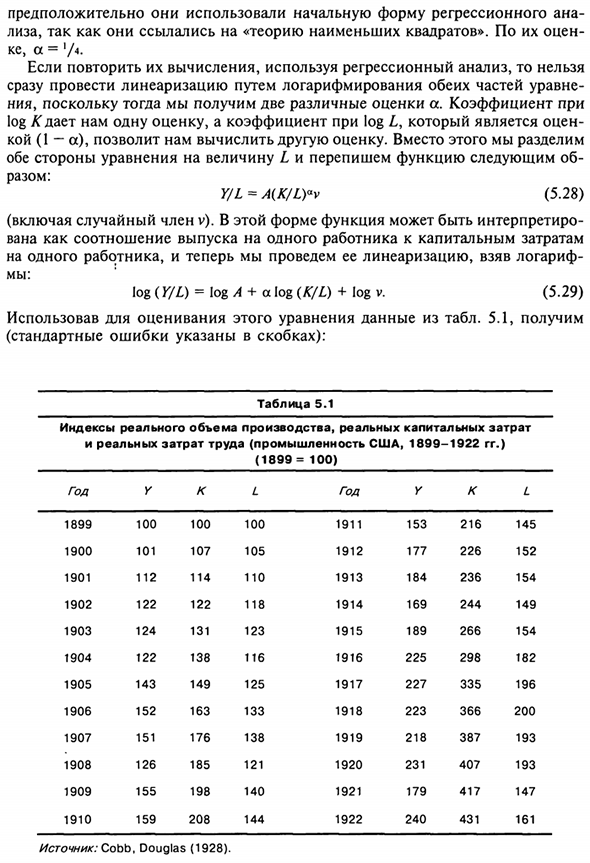
5.1, мы получаем (Стандартная ошибка показана в скобках): Таблица 5.1 Индикатор реального выпуска и реальных капитальных затрат Реальные затраты на рабочую силу (промышленность США, 1899-192, 2 года) (1 8 9 9 = 100) год Источник: Кобб, Дуглас ( 1928) log Y / L = 0,02 + 0,25 log K / L \ R2 = 0,63; (5,30) (0,02) (0,04) / = 38,0. C. Проверьте расчет Кобба. Кобб — Дуглас, конечно Это частный случай более общего выражения. Y = AK * Lb, (5,31)
Данные из таблицы используются для оценки этого уравнения. Людмила Фирмаль
Когда показатели эластичности производства для капитальных и трудовых затрат не связаны Между нами Оценивая, используя те же данные, Получено (стандартная ошибка показана в скобках): log Y = -0,18 + 0,23 log K + 0,81 log L; R2 = 0,96; (5,32) (0,43) (0,06) (0,15) F = 236,1. Это связано с тем, что эластичность на выходе достигается за счет капа тала — 0,23, что очень близко к предыдущей оценке и эластично.
Стоимость рабочей силы составляет 0,81, что немного выше предыдущей оценки. Равно 0,75. упражнения 5.5. Оценка логарифмической регрессии стоимости жилья Пастбища, располагаемый личный доход и относительные цены на эти услуги Используя данные, приведенные в упражнении 5.2, вы получите следующие результаты: таты: log >> = -1,60 + l, 181og; t-0,34 log /). Интерпретировать это уравнение.
Сравните с данной интерпретацией Ноа 5.2 для практики. Что ты имеешь ввиду? 5.6. Оценить аналогичный логарифмический регресс между расходами Продукт личного дохода от упражнения 2.4 И относительная цена товара. Интерпретировать результат. Производственная функция kbba свойства ~ -Дуглас & * ‘£ * •; «‘». —.-, — ^ — h • ‘• * •. •: • * • <-: •••; ,.
В упругом поле выхода продукта ^: влияние массы кислорода Ожидаемая доля производственных штабов и факторов производства Тори мы используем более общие функции и будем игнорировать Тыкать случайных членов; Эластичность продукта Эластичность выпуска капитала и труда Ответственно а и р dY / bK = A (a [K «~ l]) & Горячий / холодный AKa-W * ‘ 144 Точно так же легко показать, что (dY / dL) / (Y / L) равно p.
В результате увеличение капитальных вложений на 1% приводит к увеличению Производство в процентах и рост затрат на рабочую силу на 1%: * Выход увеличивается на р процентов. Можно предположить Количество как a, так и (3 находится между нулем и единицей. Позитив из-за увеличения производственных затрат Фактор должен вызывать увеличение выпуска.
Возможно в то же время Они будут меньше единства, потому что разумно предположить По мере уменьшения масштабов производства Рост производства медленнее, чем себестоимость Факторы и другие факторы остаются постоянными / Влияние масштабов производства. _ :::. :. , V? «». , ^ Если a и p в целом превышают 1, функция Влияние на масштабы производства будет увеличиваться (то есть Когда k k £ увеличивается Больший процент).
Если их сумма равна ^ E Unit 5, это примерно> Определенное влияние на масштабы производства Та же пропорция, что и у Аги I), если их сумма меньше той же ;; Имеет эффект уменьшения масштабов производства (Уувели Производится с более низкой скоростью, чем K и L. Например, предположим, что K и L удвоены. Тогда новый уро Скорость высвобождения (U) описывается следующим образом:
Γ = A (2X) ((2L) & -A2 * K * mS> = 2 + + * AK D D * 2 << * Y. » Если a + p = 1.2 и a 2 «+ P = 2.30, Y увеличивается более чем в два раза. Для a-b p = 1,0 и 2a + p = 2 удвоение K и Z удваивает Y. Для a + p = 0,8 и 2a + P = 1,74 Uuuvl | увеличивается менее чем в два раза. С первой статьи. Кобб и Г.Г. Дуглас Соотношение (5.27), которое изначально предполагалось постоянным «Новый масштаб доходов.
Тогда они ослабляют это предположение ^ „ Мы предпочитаем оценивать степень выручки по масштабу производства. Ожидаемая доля факторов производства, _. ‘^% V Согласно предположениям конкурентного рынка Канавки для производства a и b% p <6- Ожидаемый доход от каждого Кормление и труд. Если рынок труда конкурентоспособен.
Ставка заработной платы (ш) равна предельному продукту труда «(EU / E1): ‘••’ * = Щ- = АК% $ -Х = Ц-. — • ‘•• P.-,. .., ч … … 145 В результате общая сумма заработной платы ^ (w £) составляет (Давайте разделим трудозатраты на память и общий выпуск продукции / л) Определенная сумма (3. Отображается в dY / dK: /> «-V», .-. Следовательно, валовая прибыль (р ф ^^ Это была константа.
С его пылкой работой. Крбб ^ й П. Дуглас — это процент рабочей силы Трехмерное измерение, предсказанное оценкой, I ^ ^ iT. ^ Есть много проблем с использованием такой Funedia, особенно Но если он используется, см. ^ Еще в cf еще и т. Д. ^^^ В частности, даже когда: vtus * p ^ Производственное оборудование и данные Трудомода ододобо данные ^^
Есть технические процессы, которые зависят от него; ^; Т ^ сшщщщ & щд ^ щ- Важно, чтобы такие зависимости существовали <dda ,; krgda! 5PSh, Эти факторы будут объединены по следующей шкале DSI Во-вторых, даже если такая зависимость от экономики более эффективна; Если нет оснований полагать, что это будет * ^ ^ o ^ Стой форма.
Смотрите также:
| Обнаружение гетероскедастичности | Свойства коэффициентов множественной регрессии |
| Что можно сделать в случае гетероскедастичности? | Мультиколлинеарность |
Если вам потребуется заказать решение эконометрики вы всегда можете написать мне в whatsapp.

