Оглавление:







Многопролетные неразрезные балки. уравнение трех моментов
- Многопролетные неразрезные балки. Формула трех моментов Последовательность балок сидит на двух или более опорных петлях в середине. Такие балки широко используются в различных конструкциях и относятся к ряду статически неопределимых. Для риса. На рисунке 414 показана балка, опирающаяся на Т-образный шарнир. Одна из опор является шарнирно-неподвижной для восприятия осевых нагрузок, другая-шарнирно-подвижной, и балка
может свободно изменять свою длину при изменении температуры. Поддержка нумеруется слева направо, указывая самую левую цифру 0.количество пролетов определяется количеством правых опор, которые ему принадлежат. Имейте такую же вертикальную реакцию полагаясь на поддержке шарнира Т. Поскольку существует только два состояния равновесия, такая система (tn—2) статически неопределима. Как видно, число ненужных соединений, а следовательно, и ненужных реакций равно числу промежуточных опор. Иногда крайнее доверие Делается это в виде щепотки.
В этом случае степень статической неопределенности возрастает Людмила Фирмаль
по сравнению с шарнирными опорами. Чтобы получить основную систему, можно удалить все промежуточные опоры и заменить их действие неизвестной реакцией XY x2…In помимо указанной нагрузки, к основной системе прилагается КП-2 (Рис. 415). Дополнительное уравнение перемещения A|=0; A2=0 ″ •••’A/l-2=0 представляет собой условие, равное нулю отклонения в точке крепления промежуточной точки опоры. Но этот метод расчета трудоемкий, 413∞в каждом уравнении перемещения содержатся все неизвестные требуемые силы. Гораздо выгоднее строить основную
систему, размещая шарниры в секциях на всех промежуточных опорах(рис. 416). Ненужные неизвестные в этом случае будут сгибать момент к опоре балки. Таким образом, эквивалентная система представляет собой ряд простых поворотных опорных балок с заданной нагрузкой и неизвестным изгибающим моментом Afj=M2=•>L4l -| — / — HL — / — b • • •» Рис четыреста пять Применяется в секции, где установлен шарнир. Предполагается, что направление момента для определенности является положительным. Если выбрана эта основная система, указанное поведение нагрузки
- применяется только к пролету, на котором оно применяется; Четыреста шестнадцать риса Рис сорок семь Другой пролет ее ПА представлен опорным изгибающим моментом M(. Теперь сформулируем дополнительное уравнение перемещения. Они выражают равенство нулю смещения опорной части в направлении действия МЗ в неизвестный момент времени. Фактически каждая вторичная опорная балка основной системы под действием заданной нагрузки и опорного момента деформируется независимо от других. Это конец двух соседних Бало-чек, примыкающих к одной из опор, например, р-й(рис. 417), может поворачивать D G и D «º a» на определенный угол. В исходной статически неопределенной
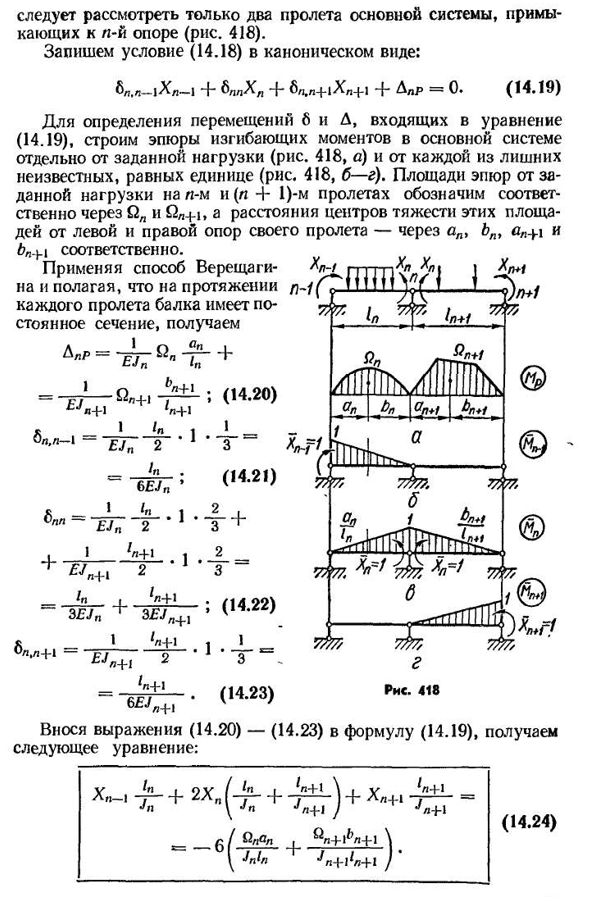
системе каждая пара таких секций представляет собой одну секцию, так что их взаимный угол поворота из непрерывного условия равен нулю, следовательно, каждая промежуточная опора D » =D G4-D G B=0. (14.18) Поскольку основная система состоит из двух несущих балок, независимых и не связанных между собой, то для раскрытия условий(14.18)) Необходимо рассмотреть только два пролета основной системы, Соединенных с 414n-й опорой(рис. 418). Запишите условие(14.18) в каноническом виде:^p. n-jXn-1+6P «xya4-6P», 4-1HP+1+LPR=0. (14.19) для определения перемещений, входящих в уравнение (14.19) 6 и D, постройте график изгибающих моментов основной системы отдельно от заданной нагрузки
(фиг. 418, С) и от каждого из дополнительных неизвестных, равных Людмила Фирмаль
единице(рис. 418, б-д). Площадь участков n-m и (l+1)-m пролета от заданной нагрузки соответственно через Q»и Q»+i, а расстояние центра тяжести этих участков, его пролет-через AP, BP-соответственно. Если применить метод Верещагина и предположить, что балка имеет определенное поперечное сечение на протяжении каждого пролета、 ^p’P~1= ~ ET^~2 1—- k_ J ВЯ _ П2 3Р■а±л. Джей, 2=2 3 ЛН+л 3jn+л Если вы добавите 1ci-H n+i2=6£7L+1 выражение (14.20)—(14.23) к выражению (14.19: ^1 и Я ЛН+т ф НН ЭДЖ+ — £Т- _ /» 3jn 6/м-н — £Дж + В/н т^н+ф Лето bn+1 (14.22) (14.23) мы самые лучшие! (14.20 утра)) Zn+I М и1. ■ 1 — ’ т — & Х», Л — +2Х» Джей Н Я в-н+^»Г Л Л-Н——•’»4-1 (14.24) 415 при таком выборе основной системы все лишние неизвестные находятся в Формуле (14.24), она принимается вместо X и изгибает момент к опоре балки.、- И так оно и есть., (14.25))
Выражение (14.25) называется выражением трех моментов. Мы вводим петли, чтобы сформировать основную систему. Чтобы записать эти уравнения, достаточно в Формуле (14.25) дать индексу Р последовательно значения 1,2, 3 и т. д., Соответствующее числу промежуточных опор. Каждое из этих уравнений содержит три и более неизвестных опорных момента L1p], m», а также первое и последнее уравнения, и не более того-только решения этих двух систем легко выполнить методом последовательного устранения неизвестных. М н-iln4~2МП (/»~/~ЛН+л)+= Л-С-Л-С’»+»)’ (14.26) Рассмотрим пример составления уравнения из трех моментов. Для риса. 419 показывает двухпролетную балку. Система не однажды определяется статически. Промежуточная помощь сразу же, что было моментом уравнения/. Если принять выражение (14.26)n=1, то существует M olt+2L4, (/,+/2)+M2/2=-6. (14.27) поскольку крайняя
левая опора шарнирно закреплена и не нагружена сосредоточенным крутящим моментом, МО=0. 416moment крайней правой концевой опоры равно времени нагрузки, приложенной к консоли. И так оно и есть., Lll12-2. Очевидно. / 1=л-п КР; г ф т+ф; / *2 —- • а т М,=4-П -^ =- г (//+с):= О-2 — b » 2 3 8 12 12 * _ /, Два. • Таким образом, выражение (14.27) принимает вид,.?’з++Т’ А2 = Б2= -±- Шесть. / Ped4+с\6л Зет Два.. Отсюда легко найти moment/I1. Если левый край балки защемлен(рис. 420, а) могут быть заменены дополнительными пролетами с бесконечно большой жесткостью, защемлением или бесконечно малым пролетом для 1-й и 2-й опор следующим образом( (/, + /2) + ^2^2 == =К2=0; Длина (рис. 420, б). Уравнение б Четыреста
двадцать риса Mj / g4-2L12 (^2+^z)L1z / 3 — = — 6 Очевидно. УГ=*3 = −7 — ; Кроме того, нужно поставить=0 в первое уравнение системы. Затем +2L42(Z2+Z3) −6. Аналогично, если правый край балки защемлен. 14 8-2770 417 опорные моменты, расчет реакций, построение фигур изгибающих моментов и боковых сил обычным способом. Сначала определите реакцию опоры каждой простой балки от заданной нагрузки и опорного момента. Мы показываем эти реакции на l-й полет через AP и VP(рис. 421, а). Это очевидно А-Л° — Л М Н-М Н-1. Мне 7 лет. » * л ВП-в°-р-м р ^ м^, (14.28) * л Вот, » — только реакция от определенной нагрузки на пролет. Полная реакция промежуточного носителя Р (фиг. 421, б» В; — в»+L._,-/g; — MP-m,.
(Йорк) Где Rn=VP+ — реакция опоры l, вызванная действием заданной нагрузки, добавленной к пролету 1P и/l+]. После определения реакции постройте график Q и M для каждой второй опорной балки основной системы. Окончательный график изгибающего момента также легко построить как сумму графика момента от нагрузки и опорного момента, последний график не поддерживается. Можно рекомендовать следующие шаги для расчета непрерывного луча. После опоры и нумерации пролетных строений (опора-от нуля, пролет-от единицы) основной Сит устанавливают под начальную балку и нагружают базовыми моментами неизвестного тогда участка только М от конкретной нагрузки на пролет, для отдельных балок основной системы. Вычислите площадь Qi этих участков и ai9B
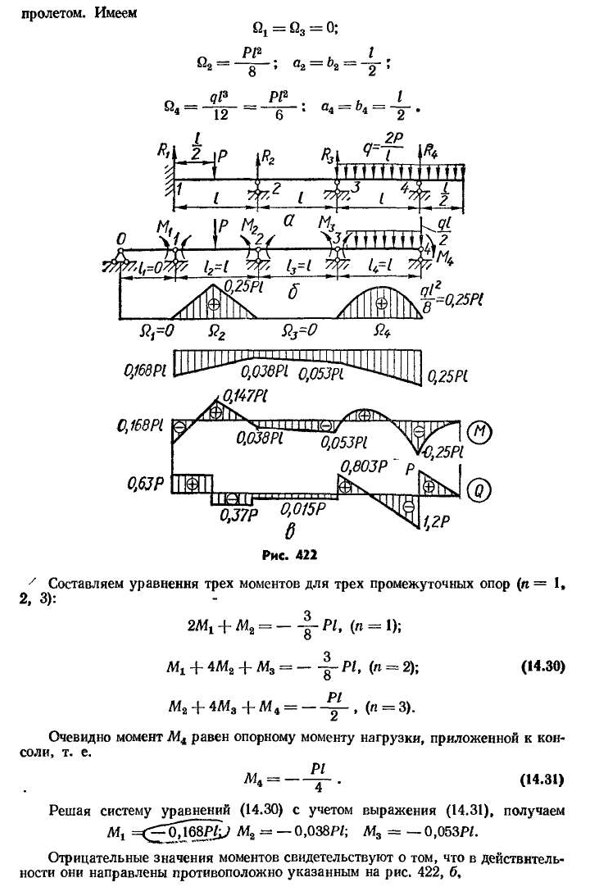
(координату их центроида. Выпишите три мгновенных уравнения для каждой промежуточной опоры. Решая полученную таким образом систему уравнений, определяется неизвестный опорный момент. Затем определяют реакцию, строят график боковых сил и изгибающих моментов. Как показано, последний график может быть построен как сумма моментов нагрузки и моментов опоры. 68, например. График изгибающего момента и поперечной силы балки показан на рисунке. 422, A. 2P Для простоты расчета используется q= — p. эти системы показаны. 422, б, зажим левого конца балки заменить дополнительным У 418 пролетом 7 составьте уравнение трех
моментов для трех промежуточных точек опоры (n=1. Три.): 2Mt+L1A= — П/, (Л=1);т+4ма+м3= — я, (» = 2); (14.30) мг+4/и3+М4=- — — — — (П=3). Очевидно, что момент M4 равен опорному моменту нагрузки, приложенной к КС-соли. МТ= — — — — — — (14.31) Принимая во внимание формулу для решения системы уравнений (14.30) (14.31), M1=<^y b8P/ym2=-0.038/7;L13=-0.053 P/. Отрицательное значение момента указывает на то, что реальность показывает свою ориентацию. 422 б, Четырнадцать.* Поддержка 419reaction(рис. 423) определить по формулам (14.28) и (14.29): A2=0.5 P+0.13 p=0.63 P; И2=0,5 с-0,1 3Р=0.37 П; Л Три. = = _0 015R; БС= — — — — М Ж~^~ = 0.015 Р; Л4=0.803 П; В,=КЖ+ «7*~=2′ 20л Четыреста двадцать три риса Реакция полной поддержки РТ=А2 = 0.63 Р; Р2-Р’2» 1 ″ −0.36 П; П8=В3 4—44=0.82 Р; Р4=В4=2.20 П. На рисунке показана фигура поперечной силы и изгибающего момента. 422, ст.
Смотрите также:
| Расчет простых статически неопределимых балок | Влияние неточного расположения опор по высоте |
| Канонические уравнения метода сил | Расчет статически неопределимых криволинейных стержней |

