Оглавление:
Многокритериальные задачи линейного программирования
Реальные проблемы, решаемые с помощью методов математического программирования, во многих случаях выдвигают несколько критериев, которым одновременно должно удовлетворять решение задачи. Причем эти критерии часто бывают антагонистическими. За последние десятилетия разработано много методов анализа и решения подобных задач. В значительной степени эти методы являются диалоговыми (или интерактивными), состоящими в последовательном анализе возможных решений лицом, принимающим решение (ЛПР), и выбором более предпочтительного решения. Методы могут основываться на предварительном выделении множества неулучшаемых (эффективных) решений и представлении этого множества ЛПР для принятия решений.
Многокритериальная задача линейного программирования (МКЛП) имеет вид:
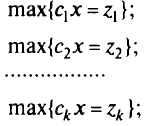
при 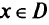 или в матричной форме
или в матричной форме
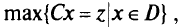
где 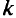 — число целевых функций (критериев);
— число целевых функций (критериев); 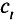 — градиент (вектор коэффициентов)
— градиент (вектор коэффициентов) 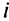 -й целевой функции (критерия);
-й целевой функции (критерия); 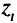 — значение
— значение 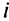 -го критерия (целевой функции);
-го критерия (целевой функции); 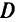 — множество допустимых значений переменных; max — означает, что нужно максимизировать все целевые функции одновременно;
— множество допустимых значений переменных; max — означает, что нужно максимизировать все целевые функции одновременно; 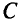 — матрица критериев размерностью
— матрица критериев размерностью 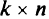 (матрица коэффициентов целевой функции, ее строки
(матрица коэффициентов целевой функции, ее строки 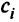 являются градиентами критериев);
являются градиентами критериев); 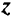 — вектор критериев.
— вектор критериев.
Предположим, что ЛПР всегда имеет функцию полезности 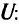
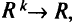 , которая отображает векторы критериев на действительную прямую так, что большее значение на этой прямой соответствует более предпочтительному вектору критериев. Функции полезности бывают разных видов: неубывающие, возрастающие, вогнутые, строго вогнутые, убывающие, выпуклые, строго выпуклые, монотонные и тл. Но исходные функции полезности могут быть преобразованы таким образом, чтобы они приняли вид, необходимый ЛПР, например, чтобы функция полезности стала покоординатно возрастающей.
, которая отображает векторы критериев на действительную прямую так, что большее значение на этой прямой соответствует более предпочтительному вектору критериев. Функции полезности бывают разных видов: неубывающие, возрастающие, вогнутые, строго вогнутые, убывающие, выпуклые, строго выпуклые, монотонные и тл. Но исходные функции полезности могут быть преобразованы таким образом, чтобы они приняли вид, необходимый ЛПР, например, чтобы функция полезности стала покоординатно возрастающей.
Многокритериальные задачи графически исследуются и в пространстве решений (как в задачах линейного программирования), и в пространстве критериев.
Пусть 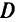 обозначает допустимую область в пространстве решений, a
обозначает допустимую область в пространстве решений, a 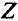 — допустимое множество в пространстве критериев. Последнее представляет собой множество
— допустимое множество в пространстве критериев. Последнее представляет собой множество 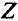 образов всех точек из
образов всех точек из 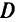 :
:
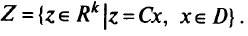
Если известна функция полезности 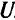 , то многокритериальная задача превращается в однокритериальную задачу
, то многокритериальная задача превращается в однокритериальную задачу
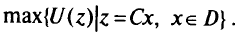
Но этот подход полезен только в концептуальном плане.
Пример:
Рассмотрим задачу МКЛП:
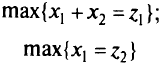
при ограничениях
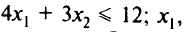
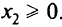
Функция полезности выбрана виде
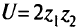
и имеет следующие выражения:
а) в пространстве решений 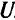
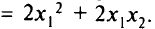 Из рис. 5.17 видно, что оптимальной точкой является точка (3,0), оптимальный вектор имеет вид (3,3), оптимальное значение
Из рис. 5.17 видно, что оптимальной точкой является точка (3,0), оптимальный вектор имеет вид (3,3), оптимальное значение 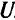 = 18;
= 18;
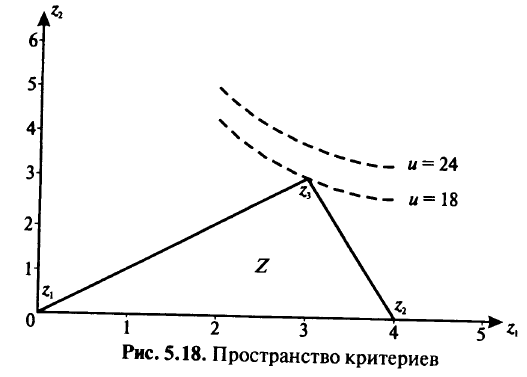
б) в пространстве критериев —
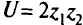
(рис. 5.18). Точка 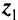 — образ точки
— образ точки 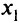 , т.е.
, т.е. 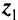 = (0,0), точка
= (0,0), точка 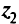 — образ точки
— образ точки 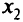 и
и 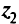 = (4,0), точка
= (4,0), точка 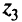 — оптимальный вектор критериев,
— оптимальный вектор критериев, 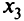 — прообраз
— прообраз 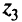 — оптимальная точка; оптимальное значение
— оптимальная точка; оптимальное значение 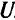 =18.
=18.
Для критериальных векторов  вводится понятие доминирования. Пусть
вводится понятие доминирования. Пусть
критериальные векторы. Вектор  доминирует вектор
доминирует вектор 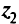 , тогда и только тогда, когда
, тогда и только тогда, когда
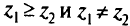
(т.е. для всех
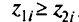
по крайней мере для одного 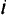 ). Таким образом, никакой компонент вектора
). Таким образом, никакой компонент вектора 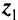 не меньше соответствующего компонента вектора
не меньше соответствующего компонента вектора 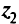 и одновременно, по крайней мере, один компонент вектора больше соответствующего компонента вектора
и одновременно, по крайней мере, один компонент вектора больше соответствующего компонента вектора 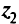 .
.
Вектор 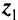 сильно доминирует вектор
сильно доминирует вектор 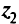 тогда и только тогда, когда
тогда и только тогда, когда 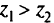 .
.
Критериальный вектор считается недоминируемым, если он не доминируется ни одним из допустимых критериальных векторов. Вектор 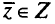 является недоминируемым тогда и только тогда, когда не существует другого вектора
является недоминируемым тогда и только тогда, когда не существует другого вектора 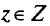 такого, что
такого, что 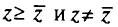 иначе
иначе 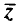 является доминируемым критерием.
является доминируемым критерием.
Критериальный вектор не может быть оптимальным, если он не является недоминируемым. И для каждого недоминируемого критериального вектора существует покоординатно возрастающая функция полезности, для которой он является оптимальным.
Доминируемость относится к векторам в пространстве критериев; в пространстве решений вводится понятие эффективности.
Точка 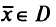 эффективна тогда, и только тогда, когда не существует другой точки
эффективна тогда, и только тогда, когда не существует другой точки 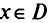 такой что
такой что 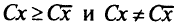 . В противном случае точка
. В противном случае точка 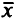 неэффективна. Точка хе D эффективна, если ее критериальный вектор не доминируется критериальными векторами других точек из
неэффективна. Точка хе D эффективна, если ее критериальный вектор не доминируется критериальными векторами других точек из 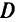 . Из эффективной точки невозможно сдвинуться допустимым образом так, чтобы увеличить один из критериев, не уменьшив, по крайней мере, один из остальных.
. Из эффективной точки невозможно сдвинуться допустимым образом так, чтобы увеличить один из критериев, не уменьшив, по крайней мере, один из остальных.
Вместе с термином «эффективность» используются термины «неулучшаемость» или «оптимальность по Парето». В практических приложениях особое внимание уделяется области Парето. Вильфредо Парето сформулировал проблему многокритериальной оптимизации в 1896 г. К этому вопросу вернулся в 1963 г. Лотфи Заде при проектировании систем управления. Область Парето задается в пространстве критериев, и любое, принадлежащее этой области решение, нельзя улучшить одновременно по всем скалярным критериям. Вне области Парето можно улучшать решение по всем критериям одновременно, но ни по одному критерию оптимальное значение здесь не достигается. Таким образом, необходимым условием решения задачи многокритериальной оптимизации является принадлежность решения области Парето, т.е. решение должно быть Парето-оптимальным, поскольку остальные решения заведомо хуже сразу по всем скалярным критериям. Однако необходима дополнительная информация, чтобы ЛПР могло выбрать единственное решение на множестве Парето-оптимальных решений. Для примера рассмотрим двухкритериальную задачу. На плоскости критериев, где задано множество допустимых решений, первый критерий достигает своего оптимума в точке А, а второй — в точке В. Кривая АВ, принадлежащая области допустимых решений, определяет для данного примера область Парето.
Множество всех эффективных точек называется эффективным множеством. Обычно легче показать, что точка неэффективна, чем доказать ее эффективность. Чтобы доказать неэффективность точки 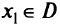 , достаточно найти другую точку
, достаточно найти другую точку 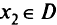 , критериальный вектор которой доминирует критериальный вектор точки
, критериальный вектор которой доминирует критериальный вектор точки 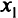 .
.
В задаче линейного программирования (ЛП) эффективная точка — это некоторая оптимальная точка, так как не должна существовать точка 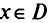 , такая, что
, такая, что 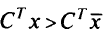 .
.
В задаче ЛП с одним критерием эффективное множество 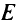 и оптимальное множество
и оптимальное множество 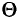 совпадают и оба выпуклы. В случае многокритериальности
совпадают и оба выпуклы. В случае многокритериальности 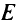 и
и 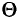 ведут себя по-разному:
ведут себя по-разному:
- Оптимальное множество может быть ограниченным и несвязным (наличие более чем одной оптимальной точки не означает, что число их обязательно бесконечно).
- В задаче МКЛП может быть более одного оптимального критериального вектора (в JIП имеется единственное оптимальное значение критерия независимо от числа оптимальных точек).
- Эффективное множество
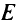 может оказаться невыпуклым.
может оказаться невыпуклым. - Оптимальная точка — не обязательно крайняя (многое зависит от вида функции полезности).
- При сведении к однокритериальной задаче с помощью функции полезности могут быть локальные оптимумы, не являющиеся глобальными.
- Оптимальное множество
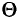 может быть пусто, когда не пусто эффективное множество
может быть пусто, когда не пусто эффективное множество 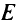 .
.
Для решения задач МКЛП применяются различные методы сведения к одному скалярному критерию: метод взвешенных сумм, методы сжатия допустимой области, метод е-ограничений, алгоритмы векторной максимизации, различные интерактивные процедуры и т.д. Процедура сведения задачи к одному скалярному критерию с помощью функции полезности очевидна. Рассмотрим другой метод сведения к одному скалярному критерию — метод взвешенных сумм с точечным оцениванием весов.
Эта теория взята со страницы лекций по предмету «математическое программирование»:
Предмет математическое программирование
Возможно эти страницы вам будут полезны:
| Комбинированный метод внутренней и внешней точек |
| Метод проекции градиента |
| Метод взвешенных сумм с точечным оцениванием весов |
| Сжатие множества допустимых решений |

