Оглавление:
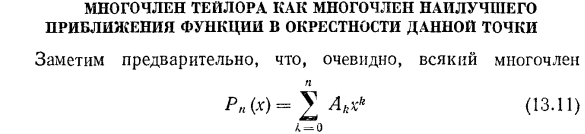


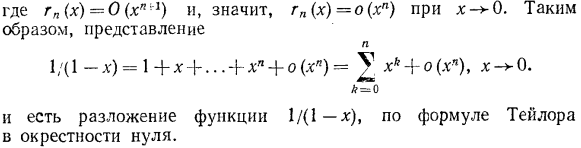

Многочлен Тейлора как многочлен наилучшего приближения функции в окрестности данной точки
Многочлен Тейлора как многочлен наилучшего приближения функции в окрестности данной точки. Во-первых, очевидно, все многочлены для x0 вы можете представить его в следующем виде На самом деле, в(13.11) достаточно поставить x = x0Φk и расширить правую часть силой H. То есть была получена формула (13.12). Точнее, выполняются следующие теоремы. Теорема 2.Пусть функция x всесторонне дифференцирована в точке x0 до степени n.
Полином Тейлора степени n является оптимальным полиномом среди всех полиномов степени n, которые аппроксимируют «бесконечно малую окрестность» точки x0, то есть функцию в x-x0. Людмила Фирмаль
- То есть полиномиальный многочлен Порядка n, отличный от полинома Тейлора Порядка n, Порядка N меньше n, не может быть аппроксимирован x * x0 (следовательно, чаще всего эта функция в пределах o ((x-x0) ’r)). (x-x0) B), K N) о высокой точности. Доказательство. Из формул (13.5) и (13.13)、 Затем, если вы передадите как X-x0 до предела, вы получите a0 = {x0).Отбросьте этот термин слева и справа и уменьшите оставшиеся выражения в обеих частях на x-x0(xfx0)、 Опять же, если вы передадите его до предела как x-x0, это будет a1 = f ’(x0).
- Если вы продолжите в том же духе. Единственность представления функции в виде (13.13) иногда используется для расширения функции по формуле Тейлора. То есть, если мы можем получить выражение (13.13) каким-то косвенным образом, мы можем утверждать, что это развертывание по выражению Тейлора (13.5), по теореме 2.То есть коэффициенты многочлена выражаются формулой (13.14). Так, например, соотношения (13.12) являются разложением многочленов (13.11) по формуле Тейлора, в данном случае r ^(.\)= 0.
В частности, если разложить полиномы степени n по формуле Тейлора, то остаток n-го порядка будет равен нулю. Людмила Фирмаль
- So, согласно теореме 2, вид многочлена (13.12) имеет вид Подобный этому В частности, если разложить полиномы степени n по формуле Тейлора, то остаток n-го порядка будет равен нулю. По формуле Тейлора функция f (x) = 0 в окрестности точки x0 = 1.Предположим, что вам нужно расширить /(1-x) обратите внимание, что 1 /(1-x) это просто сумма бесконечной геометрической прогрессии рН (х)= хп + 1xn + 2 + … = , / x / 1, получаем Где rn(x)= 0(xn’L), а следовательно, rn (x)= o (xn) как x-0.Поэтому выражение Затем происходит разложение функции 1 /(1-x) по выражению Тейлора в окрестности нуля.
Смотрите также:
| Обобщение правила Лопиталя. | Примеры разложения по формуле Тейлора. |
| Вывод формулы Тейлора. | Вычисление пределов с помощью формулы Тейлора (метод выделения главной части). |

