Оглавление:






Миогопролетные неразрезные статически неопределимые балки
- Миогопролетные непрерывные статические неопределенные пучки Непрерывная многопролетная балка-это статическая неопределенная балка, которая зависит от двух или более опор. В таких балках изгибающий момент распределяется более разумно по сравнению с расщепленной балкой. Вся поддержка как луч может захватить
позитв и недостаток обе стороны поддержки. Одна из опор в сплошной балке должна быть закреплена обязательно шарнирно, чтобы обеспечить неподвижность горизонтальной балки и воспринимать горизонтальную реакцию.
Шарнирно подвижный, Людмила Фирмаль
который нуждается во всех других опорах. Категория непрерывных балок также является двутавровой балкой с фитингами на одном или обоих концах. Степень статической неопределенности сплошной балки, в которой все опоры шарнирно закреплены, равна числу
промежуточных опор. Рисунок 124: расчет непрерывной балки позволяет применять метод сравнения деформаций, но этот метод также очень громоздок для трехпролетной балки. Гораздо проще рассчитать непрерывную балку и принять дополнительный
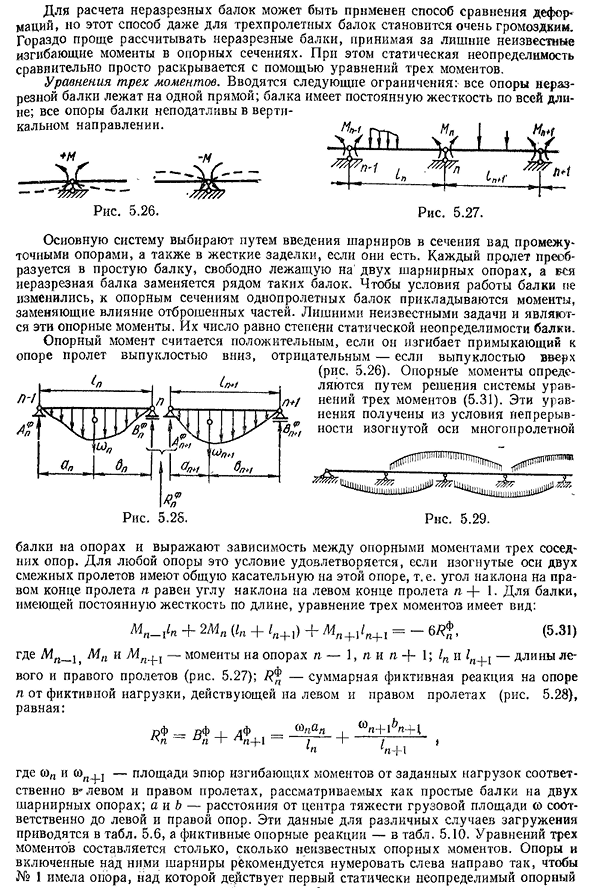
- неизвестный изгибающий момент в опорном сечении. В этом случае статическую неопределенность относительно легко выявить с помощью уравнений трех моментов. Уравнения, которые отслеживают моменты. Вводятся следующие ограничения: все опоры сплошной балки находятся на одной прямой, балка имеет определенную жесткость по всей длине, а все опоры балки неподвижны. Основная система выбирается путем введения поперечного шарнира на средней опоре пыжа, если таковой имеется, а также жесткого уплотнения. Каждый пролет трансформируется
в простую балку, свободно лежащую на двух шарнирных опорах, а вся поперечная балка заменяется рядом таких балок. Чтобы гарантировать, что условия работы балки не изменяются, момент, приложенный к опорному участку однопролетной балки, заменяющей удар отброшенных частей, лишних неизвестных материи, является моментом этих опор. Их количество равно степени статической неопределенности луча. Опорный момент считается отрицательным, если согнуть пролетное строение,
примыкающее к опоре, выпуклой стороной вниз и выпуклой стороной вверх(рис. 5.26). Опорный момент определяется решением уравнения Людмила Фирмаль
упругости Три очка (5.31). Эти уравнения выводятся из условия непрерывно изогнутых многопролетных осей. РНС 5.29 Выражена зависимость между балкой на опоре и моментом опоры трех соседних опор. То есть наклон на правом конце пролета n равен наклону на левом конце пролета ft+1. Для балки с определенной жесткостью по длине формула трех моментов такова:+2M «(ln+Z » +1)+Mn+i ln+l=-62?, (5.31) где Mp_1,момент на MP I-опоры p-1,p и p+1;1P p1P^ — длина левого и правого пролетов(рис. 5.27); 2? — Суммарная
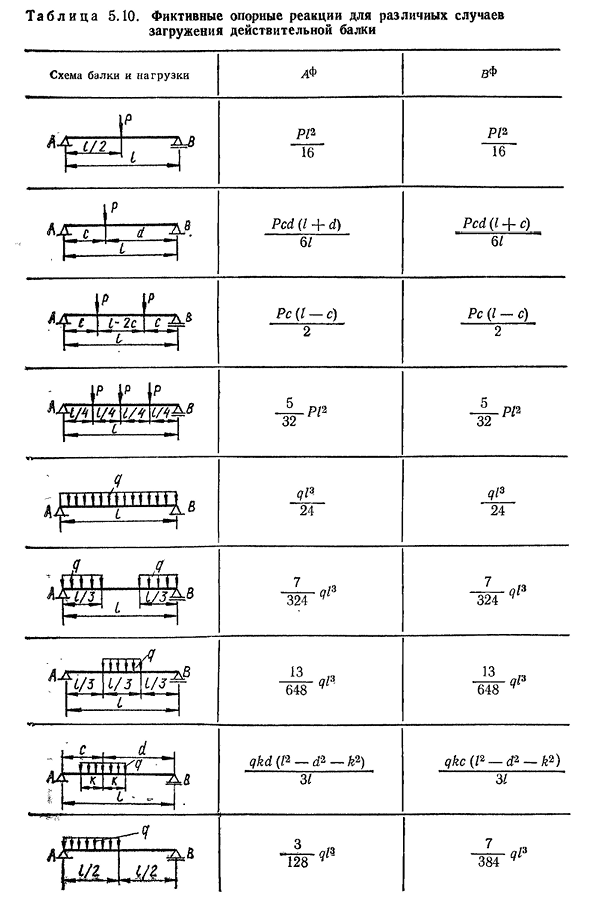
гипотетическая реакция опоры р от фиктивных нагрузок, действующих в левом и правом пролетах (рис. 5.28) равно: п f_pF|НЧ р-р-/-1-;Если j1P1P+1 Где YP I-площадь участка изгибающего момента от заданной нагрузки, а в левом и правом пролетах рассматривается простая балка на двух шарнирных опорах. эти данные для различных случаев загрузки A и b приведены в таблице. 5.6, а фиктивная ссылка реакции-на таблицу. 5.10 существует столько мгновенных уравнений, сколько неизвестных моментов поддержки. Поддержите
и пронумеруйте шарниры которые включены на нем и No. It рекомендуется, чтобы первая статически индетерминированная поддержка имела рабочую поддержку в 1. 125Т а б л и Ц А5. 10. Вымышленная реакция опоры на различные случаи фактического нагружения балки Как работают Луч и нагрузка И /ОАО ПК (Я-С)2 Пед(я+с) п р О Д О Л Ж Е Н И Е Т А Б Л. 5. Десять. Но Квадратная Лунная парабола qP Двадцать. Д-р. Двадцать. М Как Три. МИ6 Я 127П Р О Д О л ь ш е н и Е табл. 5. Десять. Схема балки и нагрузки ДФ * М Мэриленд МВ2 Момент. Поэтому крайняя левая шарнирная опора
нумеруется до нуля, а момент MP, содержащийся в первом уравнении, имеет нулевые или заранее известные значения (например, каждая из трех мод консора соединена с двумя соседними пролетами опорного момента, а спастичность связана с опорой, расположенной между этими пролетами). 5.29). Чтобы создать трехмоментную формулу опоры, часто заменяют эту опору шарниром и вводят дополнительный пролет (рис. 5.30). Рис в 5: 30 вечера. Этот промежуток не загружен, и его длина равна нулю. Когда левый конец балки защемлен, шарнирная опорная часть основной системы,
которая заменяет это защемление, находится под номером 1, и первое уравнение принимается равным n=1, Mo=0, 0: 2L41/1+M212=-6(5.31) ’2′ Если правый край балки зажат, то записывается и последнее уравнение. Если момент инерции участка, который постоянен по длине каждого пролета, отличается в разных пролетах, то формула для трех моментов выглядит следующим образом: Где Jn-размах момента инерции (относительно опоры n) левого и правого участков, а другое обозначение-то же самое. Процедура расчета непрерывного луча. 1. Для всех промежуточных опор (если уплотнение, а также до конца) вводятся шарниры и добавляются поддерживающие времена. 2. Каждый пролет непрерывной балки действует в пределах этого пролета при изгибе от заданной внешней нагрузки L4®и
шарнирной опоры 3.построена диаграмма поперечных сил. Вычисляется площадь участка L1®(грузовые зоны co) и определяется местоположение центроида a и центроида B. 4. Было составлено уравнение трех моментов. 5. Для определения неизвестных опорных моментов решается система уравнений трех моментов. 6. Определена эталонная реакция данного непрерывного пучка: — ^- в;+Л;+,+—П(5.33) 128gde I-реакция от пролетных нагрузок правой опоры левой балки и левой опоры левой балки; реакция от двух других составляющих-моменты опоры (рис. 5.31). Статическая неопределенность становится очевидной. Дальнейшие расчеты
обычно идут. 7. Изгибающий момент был решен, и сюжет был построен. Изгибающий момент при любом сечении х сплошной балки определяется по формуле: М x=Л4°м я ООН*)•(5.34) График изгибающего момента получается суммированием графика опорного момента и графика простого балочного (пролетного) момента от нагрузки пролетного строения М°8. Определяются боковые силы и строится их график. Формула для определения поперечной силы на поперечном сечении x n-го пролета сплошной балки: QX=Q°+AQ. (5.35 утра)) График поперечных сил получается из графика Q°путем суммирования»аддитивных», учитывающих влияние опорного момента: M n-M n_g Д<2= —— ,——— 9. Правильность принятого
решения проверяется. Криволинейная ось непрерывной балки непрерывна на опоре, то есть взаимный угол поворота секции влево и вправо от опоры равен нулю. График в двух соседних пролетах непрерывной балки корректен, если алгебраическая сумма мнимой реакции на нагрузку является конечным графиком M’x). Такая проверка должна выполняться столько же раз, сколько и статически неопределенная балка. Следует отметить, что сумма проекций всех сил (нагрузок и опорных реакций) равна нулю, что в данном случае является необходимым, но недостаточным условием. Если существует много пролетов, мы можем рекомендовать следующие методы
и упростить решение уравнений трех моментов(точка 5). Для K-пролетной балки мы имеем K-1 уравнение трех моментов: Рис 5.31 в поддержку среднего n равен нулю (вымышленный) Ui+1%)+ ’ ^a-2=C1> * W|4 + 2/I2(12 4-Z3) — | — L4313-C2;+2M3 (Z3+(4)+M4 / 4=C3; М k_3lk_2+2L4^3(Zft_2 4-/ох|) 4 — =С>; 2; 2^-1 + 2^/г-1(-1+4)=С К-1- Ноль четыре a2a3 е-2″ Фе-л» (И) Умножим эти уравнения на любой параметр a и сложим их параллельно. [2 (/4 4-1г) 4 — ^2А Г1 4 ″ [4A1H-2(4-4)Z3ct3]41г 4-1-1 1 * ’+2(!k_t+З*)в fe_t]—c я я++c3a3+с’•+4К-1А-п(б) 5 2-256 Выберите множитель 129 a так, чтобы уравнение коэффициента MP (b) было равно нулю.■2 (it4
—|a)»I+^»2=l2af+2(12+ls)+1(z—0;C»2+Uz+h)» z+^a4—0; / ©hl—2a k—3+2(-2+h-1)параметр a больше числа уравнений, одно из которых может быть задано произвольно. Обычно это занимает 4-1. Затем решаем систему ©, находим: «2 = — 2 + 1) ; «z=-2 (A-+1)a2-a4. В общем = — 2 — + 1 / да., _ , ————— а » 2. После вычисления параметров A напишите уравнение (ft): к-1 [^«1г-2+2У к-1+а-Фе-11^К-Л=2CIA’и’ г=1 Отсюда мы находим момент прямой ссылки К-и k~ ’ lk-la k-2+2UK-l+lk) определяем момент из последнего уравнения системы a_l (и)находим момент Mk_2, из последнего момента M k_3 и т. д. Поэтому каждый раз нужно решать одно уравнение с одним неизвестным (см. Пример расчета).
Смотрите также:
| Определение перемещений в балках переменной жесткости | Определение деформаций статически неопределимых балок. |
| Статически неопределимые балки | Расчёт неразрезных балок. |

