Оглавление:
Для каждого элемента определителя можно вычислить его минор.
Минором элемента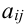 
определителя 
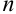-го порядка называется новый определитель порядка 
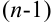, полученный из данного вычеркиванием 
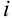-й строки и 
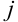-го столбца, на пересечении которых находится элемент .
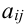Минор элемента 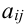обозначают 
.
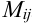Пример №2.4.
Найдите все миноры определителя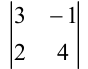 
Решение:
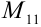получаем вычеркиванием из определителя 1-й строки и 1-го столбца; 
;
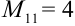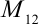получаем вычеркиванием из определителя 1-й строки и 2-го столбца; 
;
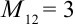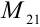получаем вычеркиванием из определителя 2-й строки и 1-го столбца; 
;
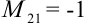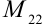получаем вычеркиванием из определителя 2-й строки и 2-го столбца; 
.
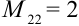Ответ: ; ; ; .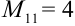
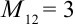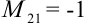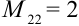Пример №2.5.
Найдите миноры элементов второй строки определителя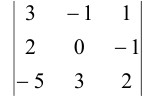 
Решение:
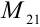— получаем вычеркиванием из определителя 2-й строки и 1-го столбца:
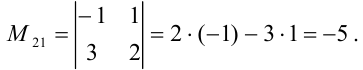
Аналогично:
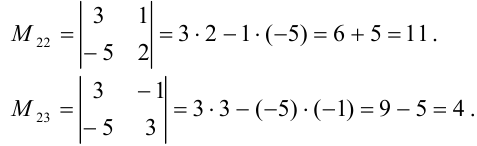
Ответ: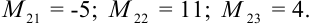 
Алгебраическим дополнением элемента 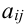называется минор этого элемента, взятый со знаком 
.
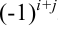Алгебраическое дополнение элемента 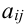обозначают 
.
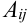Таким образом,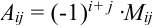 
.
Пример №2.6.
Найти все алгебраические дополнения определителя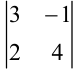 
Решение:
Воспользуемся решением примера 2.4: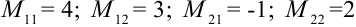 
.
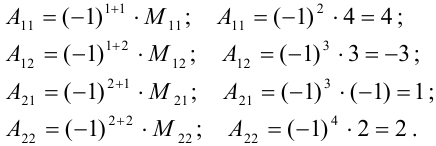
Ответ: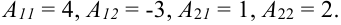 
Пример №2.7.
Найдите алгебраические дополнения элементов второй строки определителя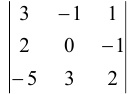 
Решение:
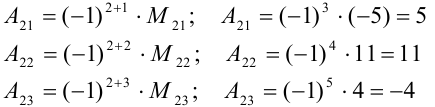
Ответ: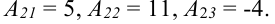 
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Понятие определителя матрицы. |
| Свойства определителей. |
| Теорема о разложении определителя по элементам строки или столбца. |
| Расчет определителей в электронных таблицах Microsoft Excel. |
