Пример №6.
Минимизация дисбаланса на линии сборки. Фирма производит изделие, состоящее из трех узлов. Эти узлы изготавливают на двух заводах. Производительность заводов по выпуску каждого из трех видов узлов не одинакова. В табл. 1.3 указаны производительность заводов по выпуску каждого из узлов и суммарное время, которое каждый из заводов может выделить в течение недели на производство этих узлов.
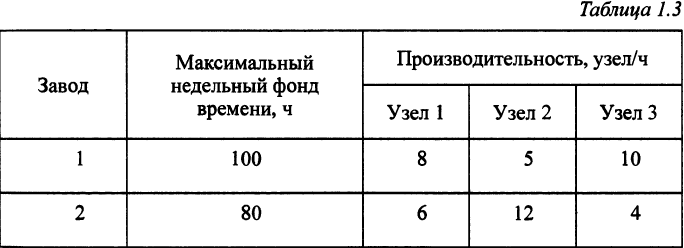
Требуется определить еженедельные затраты времени (в ч) на производство каждого из трех видов узлов на каждом заводе, обеспечивающие максимальный выпуск изделий.
Описание неизвестных. Обозначим через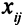 
недельный фонд времени (ч), выделяемый на 
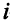-м заводе для производства 
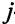-го узла,
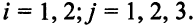
Всего в задаче 6 переменных.
Описание целевой функции. Определим, сколько узлов каждого вида поступит на линию сборки в течение недели.
Первый завод за неделю изготовит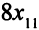 
узлов первого вида, 
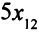узлов второго и 
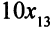узлов третьего вида. Для второго завода эти числа равны соответственно
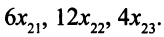
Тогда на линию сборки поступит
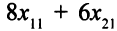
узлов первого вида,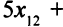 
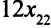узлов второго вида,
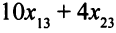
узлов третьего вида. Число готовых изделий равно минимальному из этих трех выражений. Это число требуется максимизировать.
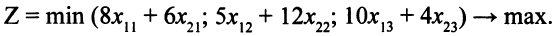
Описание системы ограничений. Время, затраченное каждым из заводов на производство всех трех узлов, не должно превышать суммарного недельного фонда времени. Поэтому
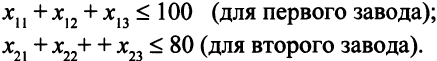
Кроме того,
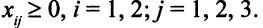
Построенная модель не линейна, так как не линейна целевая функция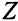 
. Целевую функцию можно сделать линейной, если положить
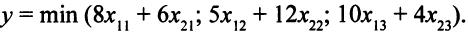
Тогда
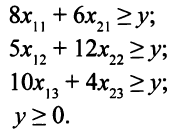
Окончательно математическую модель можно записать так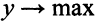 
шах при ограничениях
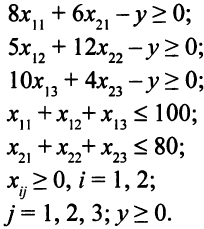
Эта задача взята со страницы решения задач по предмету «линейное программирование»:
Решение задач по линейному программированию
Возможно эти страницы вам будут полезны:
| Пример №4. Задача планирования производств |
| Пример №5. Транспортная задача. |
| Пример №7. Построить допустимую область системы неравенств |
| Пример №7. Построить допустимую область системы неравенств |
