Мгновенный центр скоростей фигуры
Скорость любой точки плоской фигуры в каждый момент времени можно рассматривать как геометрическую сумму двух скоростей: скорости полюса и скорости данной точки от вращения
вокруг полюса, причем за полюс может быть взята любая точка фигуры. Эта произвольность выбора полюса позволяет внести значительное упрощение в изучение движения плоской фигуры.
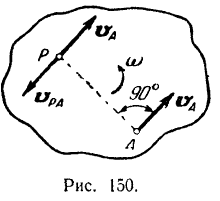
При всяком движении плоской фигуры (кроме поступательного) всегда можно отыскать такую точку, лежащую или на самой движущейся фигуре или на ее мысленном продолжении, скорость которой в данный момент равна нулю. В самом деле, пусть в данный момент скорость какой-либо произвольной точки 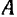 фигуры (рис. 150) равна
фигуры (рис. 150) равна 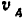 , причем направление вращения фигуры (на рис. 150 оно указано стрелкой) и угловая скорость
, причем направление вращения фигуры (на рис. 150 оно указано стрелкой) и угловая скорость 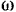 нам также известны. Восставим в точке
нам также известны. Восставим в точке 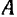 фигуры перпендикуляр к скорости этой точки так, чтобы угол 90 был отсчитан от вектора
фигуры перпендикуляр к скорости этой точки так, чтобы угол 90 был отсчитан от вектора 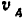 в сторону вращения фигуры, н отложим на нем отрезок
в сторону вращения фигуры, н отложим на нем отрезок
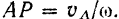
Примем точку 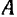 за полюс. Тогда скорость точки
за полюс. Тогда скорость точки 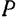 , как и скорость всякой другой точки фигуры при ее плоском движении, будет складываться из скорости
, как и скорость всякой другой точки фигуры при ее плоском движении, будет складываться из скорости 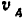 полюса
полюса 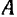 и скорости
и скорости 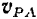 точки
точки 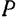 от вращения вокруг этого полюса:
от вращения вокруг этого полюса:
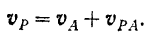
Модуль скорости 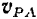 равен
равен
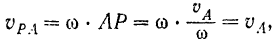
т. е. он равен модулю скорости 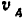 полюса. Направлена же скорость
полюса. Направлена же скорость 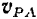 перпендикулярно к отрезку
перпендикулярно к отрезку 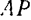 в сторону вращения фигуры, т.е. по одной прямой со скоростью
в сторону вращения фигуры, т.е. по одной прямой со скоростью 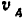 полюса, но в противоположную сторону (рис. 150). Ясно, что геометрическая сумма двух равных и противоположных по направлению векторов
полюса, но в противоположную сторону (рис. 150). Ясно, что геометрическая сумма двух равных и противоположных по направлению векторов 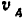 и
и 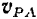 равна нулю, а потому в данный момент абсолютная скорость точки
равна нулю, а потому в данный момент абсолютная скорость точки 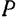
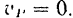
Точка 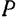 движущейся плоской фигуры, скорость которой в данный момент времени равна нулю, называется мгновенным центром скоростей этой фигуры.
движущейся плоской фигуры, скорость которой в данный момент времени равна нулю, называется мгновенным центром скоростей этой фигуры.
Мгновенный центр  скоростей фигуры, как видно из способа, при помощи которого мы нашли его положение. всегда лежит на линии, проведенной из какой-либо точки фигуры, перпендикулярно к направлению скорости этой точки.
скоростей фигуры, как видно из способа, при помощи которого мы нашли его положение. всегда лежит на линии, проведенной из какой-либо точки фигуры, перпендикулярно к направлению скорости этой точки.
Если известны направления скоростей двух каких-либо точек фигуры, то мгновенный центр  скоростей этой фигуры легко находится как точка пересечения линий, проведенных из данных точек фигуры перпендикулярно к скоростям этих точек (рис. 151).
скоростей этой фигуры легко находится как точка пересечения линий, проведенных из данных точек фигуры перпендикулярно к скоростям этих точек (рис. 151).
Найдя положение мгновенного центра скоростей 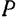 и зная для рассматриваемого момента скорость какой-либо точки фигуры не только по направлению, но и по величине, легко найти и угловую скорость фигуры, соответствующую этому моменту времени. Так как
и зная для рассматриваемого момента скорость какой-либо точки фигуры не только по направлению, но и по величине, легко найти и угловую скорость фигуры, соответствующую этому моменту времени. Так как

Угловая скорость фигуры в каждый момент равна отношению модуля соответствующей этому моменту скорости какой-либо точки фигуры к расстоянию от этой точки до мгновенного центра скоростей. Направление же вращения фигуры определяется известным направлением скорости ее точки.
Указанный выше прием определения мгновенного центра скоростей фигуры как точки пересечения перпендикуляров, восставленных к скоростям двух точек фигуры, неприменим, очевидно, тех случаях, ко;да чти скорости параллельны. При игом возможны два случая:
- Скорости двух точек
 и
и  фигуры параллельны, но эти точки не лежат на одном перпендикуляре к направлению их скоростей (рис. 152).
фигуры параллельны, но эти точки не лежат на одном перпендикуляре к направлению их скоростей (рис. 152).
Так как перпендикуляры, восставленные из точек 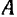 и
и 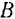 к их скоростям, не пересекаются, но мгновенный центр скоростей фигуры лежит в бесконечности. Расстояния точек
к их скоростям, не пересекаются, но мгновенный центр скоростей фигуры лежит в бесконечности. Расстояния точек 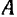 и
и 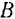 от мгновенного центра скоростей
от мгновенного центра скоростей
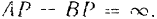
Угловая скорость фигуры и данный момент
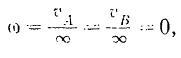
и вращение фигуры в этот момент, следовательно, отсутствует. А так как всякое плоское движение фигуры можно рассматривать как совокупность поступательного движения со скоростью произвольно выбранного полюса и вращательного движения вокруг этого полюса, то абсолютные скорости точек фигуры в рассматриваемом случае равны только скорости полюса. Другими словами, в этом случае фигура совершает в данный момент поступательное’) движение, и скорости всех се точек равны между собой.
- Скорости двух точек
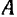 и
и 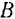 фигуры параллельны, и эти точки лежат на одном перпендикуляре к направлению их скоростей (рис. 153)
фигуры параллельны, и эти точки лежат на одном перпендикуляре к направлению их скоростей (рис. 153)
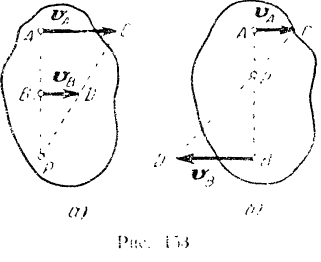
В данном случае перпендикуляры, восставленные в точках  и
и  фигуры к направлениям их скоростей, сливаются в одну прямою, и для определения положения мгновенного центра скоростей нужно знать скорости двух точек фигуры не только по направлению, по и по модулю.
фигуры к направлениям их скоростей, сливаются в одну прямою, и для определения положения мгновенного центра скоростей нужно знать скорости двух точек фигуры не только по направлению, по и по модулю.
Так как мгновенный uenip скоростей всегда лежит пи перпендикуляре, восставленном в любой точке фигуры к направлению ее скорости, а модули скоростей различных точек фигуры в каждый момент пропорциональны расстояниям этих точек от мгновенного центра, то положение точки  на перпендникуляре может быть найдено из пропорции
на перпендникуляре может быть найдено из пропорции
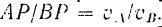
Если мы проведем через концы  и
и  (рис. 153, а и б) векторов
(рис. 153, а и б) векторов 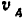 и
и 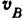 прямую, го она пересечет отрезок
прямую, го она пересечет отрезок 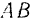 в точке
в точке 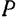 , являющейся мгновенным центром скоростей фигуры.
, являющейся мгновенным центром скоростей фигуры.
Это следует из того, что, исходя из подобия 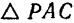 и
и 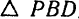 , можно составить написанную выше пропорцию.
, можно составить написанную выше пропорцию.
Нетрудно понять, что если при этом
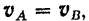
то фигура совершает в данный момент поступательное движение (так же как и в предыдущем случае).
В практических задачах часто приходится иметь дело со случаями, когда плоская фигура движется так, что ее контур катится без скольжения по некоторой неподвижной кривой. Так как в каждый момент у движущейся плоской фигуры может быть только одна точка, имеющая скорость, равную нулю, а при качении без скольжения таковой является точка фигуры, в которой она касается неподвижной кривой, то при качении без скольжения контура фигуры по неподвижной кривой мгновенным центром скоростей будет точка касания этого контура с неподвижной кривой.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:

