Оглавление:




Мгновенная изменяемость системы
- В некоторых случаях неправильное расположение необходимого количества соединений может сформировать систему и привести к бесконечному перемещению отдельных элементов без деформаций. Система, допускающая бесконечно малое относительное перемещение без какой-либо деформации ее элементов, называется изменчивой сразу же после окончания которой она становится
неизменной. Для наглядности два стержня (диска), расположенные на прямой линии, прикреплены к Земле шарнирами C и D, соединенными между собой шарниром B 27.8). Эта система имеет необходимое количество соединений, поскольку D=2, W=1 и SOP=4. B7=3-2— 2 1 -4 =0. Но от любой внешней нагрузки точка B может быть перемещена в положение B{без деформаций стержней BC и VD.
Действительно, две окружности, вычерченные из центров C и D Людмила Фирмаль
радиусом SV и DV в точках B, имеют общую касательную, перпендикулярную стержням BC и VD. Таким образом, точка B может быть трансляционно перпендикулярна радиусу SV и DV на бесконечно малую величину BBi. После перехода шарнира в положение Bi эта система изменяется геометрически неизменным образом, и вместе с землей появляются три шарнира C, B и D, которые не лежат на одной прямой. В системе, которая изменяется мгновенно
, ее элементы и силы в поддерживающей реакции неопределенны и равны бесконечности. Чтобы доказать это утверждение, я приведу пример балки, установленной на трех опорных стержнях, оси которых пересекаются в точке B (рис. 27.9, а). Этот луч изменяется мгновенно, потому что он может вращаться под бесконечно малым углом вокруг мгновенного центра вращения B. 303 страницы 27.8 Рис
- 27.9 — > 27.9, 6. Тогда эталонную реакцию можно определить по формуле статического равновесия SMfl=0, Fa-Rc r=Ot, Rc-Fa!Р Поворачивая опорный стержень с в исходное горизонтальное положение, расстояние g стремится к нулю. На пределе Дистанционное управление= Г — +ОО Когда нет внешней нагрузки F=0, мы получаем / неопределенность?С=0/0. Исследование показывает, что система, которая изменяется мгновенно, не должна использоваться для строительных конструкций. Также не следует использовать систему, характеристики которой близки к непосредственной изменчивости, так как в этом случае может
возникнуть значительное количество усилий. Поэтому при кинематическом анализе конструкции, помимо определения степени свободы и изучения геометрической структуры, необходимо проверять мгновенные колебания. В простой системе обычно выполняется тест мгновенного изменения по сравнению с известной мгновенной переменной. Если исследуемая система не является аналогом мгновенно изменяющегося стандарта, то она неизменна. Простая мгновенно изменяемая система получается следующим способом расположения дисков, стержней и шарниров. 1.
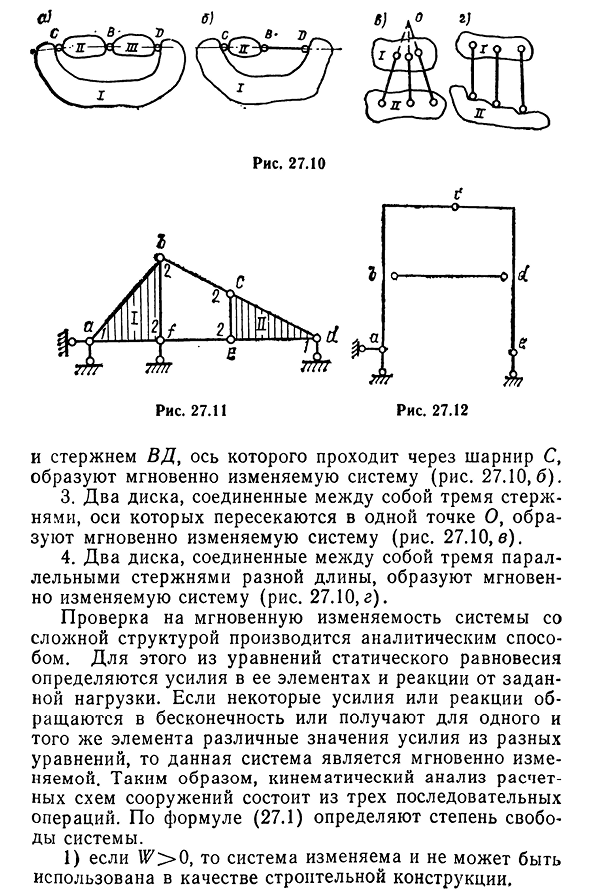
Три диска соединены тремя шарнирами на одной прямой, образуя мгновенную изменяющуюся систему(рис. 27.10 а). 2. И два диска, соединенных Людмила Фирмаль
шарнирами Стержень 804i VD, ось которого проходит через шарнир C, мгновенно образует переменную систему(рис. 27.10, 6). 3. Два диска соединены тремя стержнями, и их оси пересекаются в одной точке O, образуя систему, которая мгновенно изменяется(рис. 27.10 б). 4. Два диска, Соединенные тремя параллельными стержнями разной длины, мгновенно образуют изменяемую систему(рис. 27.10, г). Проверка мгновенных флуктуаций в системах со сложными структурами осуществляется аналитическим путем. Для этого уравнение статического равновесия определяет силу в своем элементе и реакцию от данной нагрузки. Если некоторые силы или реакции становятся бесконечными, или вы получаете разные значения силы одного и того же элемента из разных уравнений, эта система
мгновенно модифицируется. Таким образом, кинематический анализ расчетной схемы конструкции состоит из трех последовательных операций. По формуле (27.1) определяется степень свободы системы. 1) нет. >0, система переменчива и не может быть использована в качестве строительной конструкции. 20-480 В U/^O (3052) анализ геометрических структур выполняется с использованием правил формирования геометрической инвариантной системы. 3) Если система имеет геометрически неизменяемую структуру и не содержит лишних связей, проверьте ее на мгновенные колебания.
Например. Выполните анализ движения фермы, как показано на рисунке. 27.11 Решение. В этой ферме W=10, стержень D=8 и опорный стержень Spp=4 шарнира. Степени свободы U7=3D-2SH-SOP= = 3-8-2-10-4=0, то есть количество соединений, требуемых фермой. Перейдем к анализу геометрических структур. В исследуемой ферме можно выделить две геометрически неизменные части: треугольник ABF и cde на шарнире. На рисунке они заштрихованы и обозначены как диск I и II соответственно. Диск I закреплен на земле тремя непараллельными и непересекающимися опорными стержнями, то есть он является единым с Землей рассматриваемым диском I, анализируемая система состоит из неподвижного диска I, диск II закреплен опорой точки d и двух стержней (BS и E). быть Поскольку
оси этих стержней пересекаются в одной точке (точка d), рассматриваемая ферма мгновенно изменяется. Например. Может быть. 27.12 Решение. В этой раме диск D=3, простое цилиндрическое соединение W=3 и опорный стержень SOP=3. Никаких степеней свободы. =3Д-2Ш-СОП=3-3-2-3 = 0, которое имеет необходимое количество связей. Перейдем к анализу геометрических структур. Каркас в исследовании состоит из трех дисков abc, cde и bd, которые соединены тремя шарнирами B, C и D. В результате эти диски образуют геометрически неизменную систему, то есть единый диск. Этот диск установлен на земле тремя непараллельными и непересекающимися опорными стержнями. Этот фрейм является неизменным с требуемым количеством связей, т. е. чем-то статически определимым.
Смотрите также:
Решение задач по технической механике

