Оглавление:
Методы внешней точки для задачи математического программирования
Попытаемся приблизиться к оптимальной точке из недопустимой области. Для этого преобразуем достаточные условия локального минимума задачи математического программирования следующим образом:
1) рассмотрим ограничения в ослабленной форме —
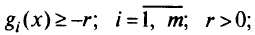
2) преобразуем условие дополняющей нежесткости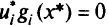 
так, чтобы оно имело смысл для отрицательных значений 
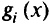и сводилось к исходному условию при 
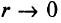(это означает, что
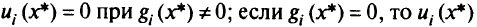
принимает любые значения), т.е.
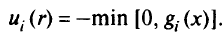
Отсюда, если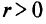 
и мало, 
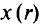удовлетворяет (5.26) 
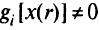для некоторых
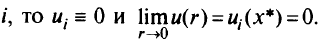
Если
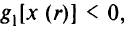
то
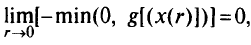
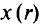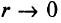так как из (5.26) следует, что точка при находится в допустимой области. В силу (5.26)
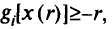
а из (5.27) вытекает, что
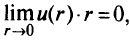
поэтому
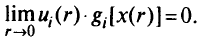
Условие дополняющей нежесткости в данном случае выполняется в пределе (из (5.27) следует, что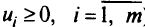 
).
Аналогично преобразуют другие достаточные условия:
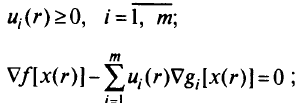
для каждого вектора у, для которого
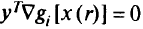
при всех
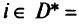
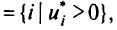
справедливо неравенство
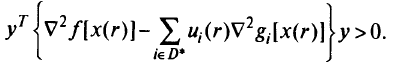
Подставим (5.27) в (5.28):
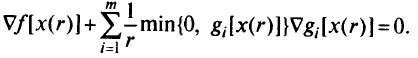
Опять непосредственной проверкой убеждаемся, что функция, для которой выполняются названные условия, имеет вид
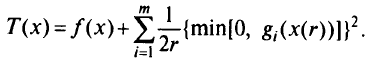
Это и есть функция, минимизируемая методом внешней точки. В нее могут входить ограничения в виде и неравенств, и равенств. Можно доказать, что все необходимые условия минимума этой функции выполняются, например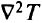 
есть положительно определенная матрица, причем для ограничений-неравенств
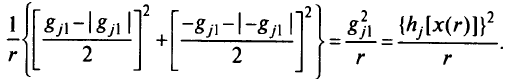
Для ограничений-равенств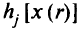 
можно записать
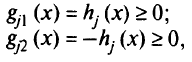
откуда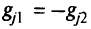 
или
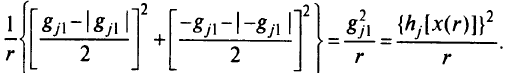
Рассмотрим пример применения метода внешней точки для решения задачи математического программирования.
Пример:
Минимизировать
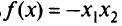
при ограничениях
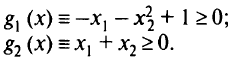
Решение:
Составим функцию штрафа для метода внешней точки:
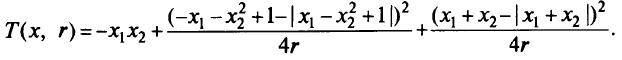
Из необходимого условия
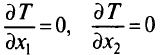
определим последовательность значении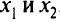 
, сходящуюся к решению.
Зададим последовательность значений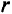 
: 1,0; 0,5; 1/3; 0,1; получим соответствующие последовательности значений:
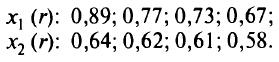
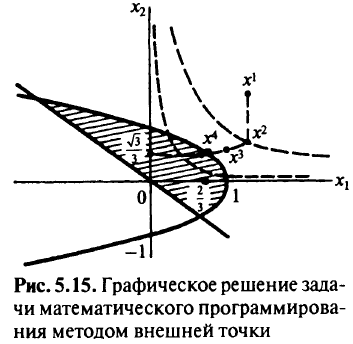
Последовательность значений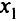 
сходится к 2/3, а последовательность значений 
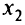к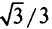 
(рис. 5.15).
Методы внутренней и внешней точек основаны на разных принципах: в первом случае штрафной член препятствует нарушению ограничений, во втором — он предотвращает блуждание точек слишком далеко от допустимой области.
Эта теория взята со страницы лекций по предмету «математическое программирование»:
Предмет математическое программирование
Возможно эти страницы вам будут полезны:
| Эвристический алгоритм решения задачи синтеза сети связи |
| Методы внутренней точки для задачи математического программирования |
| Комбинированный метод внутренней и внешней точек |
| Метод проекции градиента |
