Методы решения задач с модулями
Обратимся к рассмотрению основных приёмов и методов решения задач, содержащих модули. Их условно можно разбить на две группы.
1) Специальные приёмы раскрытия модулей, характерные именно для задач, содержащих модули:
- раскрытие модуля по определению;
- метод интервалов как базовый метод раскрытия модулей в случаях, когда подмодульные выражения содержат одну неизвестную;
- метод областей, обобщающий метод интервалов на случай, когда количество неизвестных под знаком модуля больше одной;
- раскрытие модуля с помощью его геометрического смысла;
- методы, основанные на использовании разнообразных свойств модуля (в том числе в виде неравенств, когда уравнение реализует частный случай обращения неравенства в равенство; при этом проводится анализ необходимых и достаточных условий достижения равенства);
- метод замены множителей вида
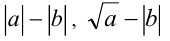 в отдельных типах неравенств на множители эквивалентного знака, не содержащие модулей и др.
в отдельных типах неравенств на множители эквивалентного знака, не содержащие модулей и др.
В частности, на некоторых из перечисленных приёмов основаны схемы решения наиболее часто встречающихся типов уравнений и неравенств с модулями.
2) Универсальные приёмы и методы, используемые не только при решении задач с модулями, но и в других разделах математики:
- возведение в степень (чаще всего, в квадрат);
- графический подход (метод координат), когда в решении используются графические образы уравнений или неравенств с модулями;
- метод замены переменных;
- метод оценок, функциональные методы и многие другие известные подходы.
Чтобы успешно решать задачи на данную тему, необходимо не только хорошо разбираться в различных методах решения, но и уметь отбирать для конкретной задачи наиболее оптимальный способ.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

