Задача 2.50.
Методом Гомори найти решение задачи, состоящей в определении максимального значения функции
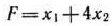
при условиях
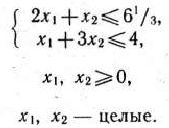
Дать геометрическую интерпретацию решения задачи.
Решение:
Сформулированную задачу перепишем так: найти максимальное значение функции
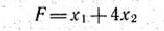
при условиях
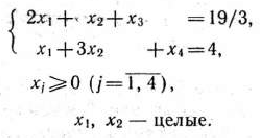
Задача (49) — (52) является частично целочисленной, так как неременные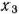 
и 
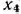могут принимать нецелочисленные значения.
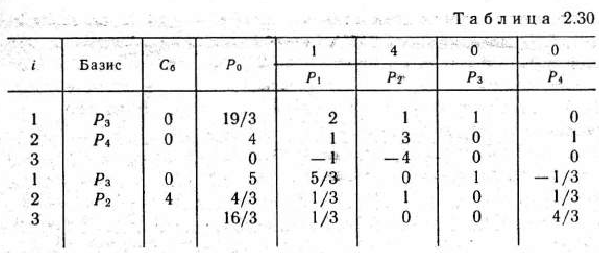
Находим симплексным методом решение задачи (49) — (51) (табл. 2.30).
После II итерации получаем оптимальный план данной задачи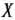 
= (0; 4/3; 5; 0). При этом плане переменная 
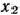приняла нецелочисленное значение. Поэтому необходимо перейти к новой
задаче, добавив к системе ограничений (49) —(51) еще одно ограничение:
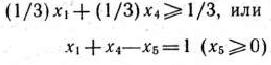
Находим теперь решение задачи, состоящей в определении максимального значения функции (49) при условиях (50), (51) и (53). Данную задачу решаем двойственным симплекс-методом (табл. 2.31).
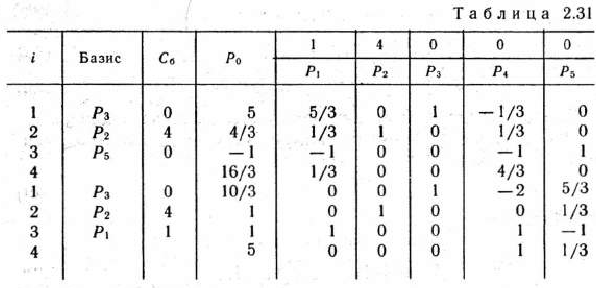
Из табл. 2.31 видно, что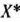 
= (1; 1; 10/3; 0; 0) является оптимальным планом построенной задачи. Так как при этом плане переменные 
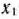и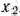 
принимают целые значения, то он также является оптимальным планом исходной задачи (49)—(52).
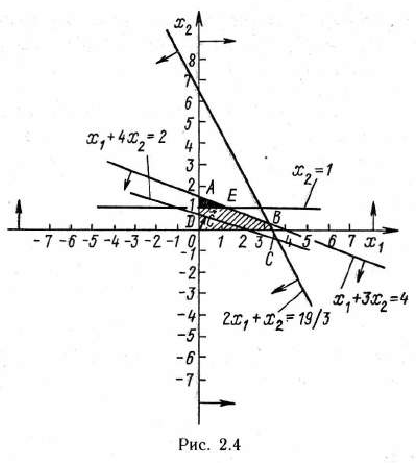
Дадим геометрическую интерпретацию решения задачи. На рис. 2.4 показана область допустимых решений задачи (49) — (51). Из рисунка видно, что максимальное значение целевая функция принимает в точке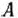 
(0; 4/3), т. е. что 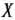= (0; 4/3; 5; 0) является оптимальным планом задачи (49) — (51). В то же время 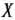=(0; 4/3; 5; 0) не является планом задачи (49) —(52). так как переменная 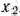принимает дробноезначение. Поэтому вводим
дополнительное ограничение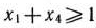 
. откуда, подставляя вместо 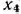его значение из второго уравнения системы уравнений (50), получаем 
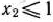. Этому неравенству на рис. 2.4 соответствует полуплоскость, ограниченная прямой отсекающей от многоугольника 
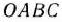треугольник 
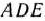. В области 
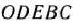находим точку 
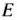(1; 1), в которой функция (49) принимает максимальное значение. Так как координаты точки 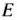— целые числа, то 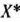=(1; 1; 10/3; 0) является оптимальным планом задачи (49) — (52). Это видно и из табл. 2.31.
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:
