Задача 2.49.
Методом Гомори найти максимальное значение функции
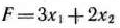
при условиях
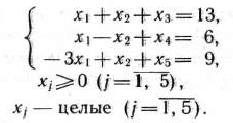
Дать геометрическую интерпретацию решения задачи. Решение. Для определения оптимального плана задачи (40) — (43) сначала находим оптимальный план задачи (40) — (42) (табл. 2.28).
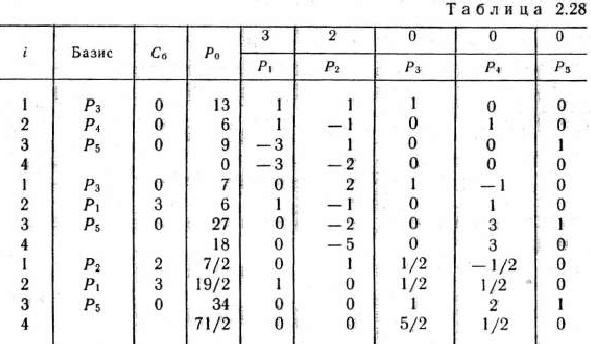
Как видно из табл. 2.28, найденный оптимальный план 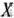 = (19/2; 7/2; 0; 0; 10) задачи (40) —(42) не является оптимальным планом задачи (40) —(43). поскольку две компоненты
= (19/2; 7/2; 0; 0; 10) задачи (40) —(42) не является оптимальным планом задачи (40) —(43). поскольку две компоненты 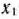 и
и 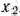 имеют нецелочисленные значения. При этом дробные части этих чисел равны между собой. Поэтому для одной из этих переменных составляется дополнительное ограничение. Составим, например, такое ограничение для переменной
имеют нецелочисленные значения. При этом дробные части этих чисел равны между собой. Поэтому для одной из этих переменных составляется дополнительное ограничение. Составим, например, такое ограничение для переменной 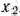 . Из последней симплекс-таблицы (табл. 2.28) имеем
. Из последней симплекс-таблицы (табл. 2.28) имеем
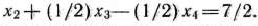
Таким образом, к системе ограничений задачи (40)—(42) добавляем неравенство
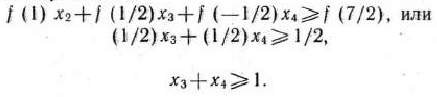
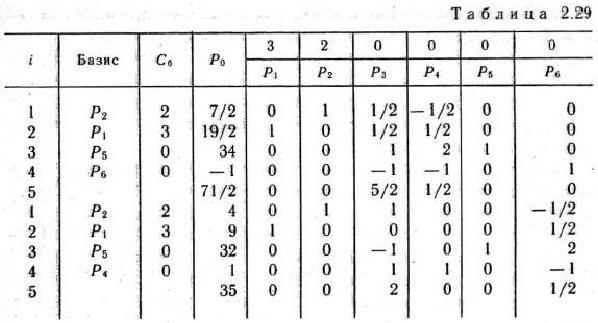
Находим теперь максимальное значение функции (40) при выполнении условий (41), (42) и (44) (табл. 2.29).
Из табл. 2.29 видно, что исходная задача целочисленного программирования имеет оптимальный план
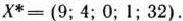
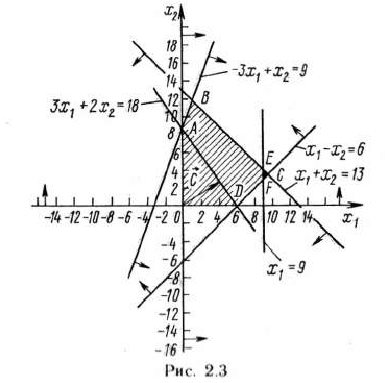
При этом плане значение целевой функции равно 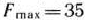 . Дадим геометрическую интерпретацию решения задачи. Областью допустимых решений задачи (40) — (42) является многоугольник
. Дадим геометрическую интерпретацию решения задачи. Областью допустимых решений задачи (40) — (42) является многоугольник 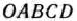 (рис. 2.3). Из рис. 2.3 видно, что максимальное значение целевая функция принимает в точке
(рис. 2.3). Из рис. 2.3 видно, что максимальное значение целевая функция принимает в точке 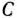 (19/2; 7/2), т. е. что
(19/2; 7/2), т. е. что 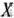 = (19/2; 7/2; 0; 0; 34) является оптимальным планом. Это непосредственно видно и из табл. 2.28. Так как
= (19/2; 7/2; 0; 0; 34) является оптимальным планом. Это непосредственно видно и из табл. 2.28. Так как 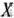 = (19/2; 7/2; 0; 0; 34)
= (19/2; 7/2; 0; 0; 34)
не является оптимальным планом задачи (40) — (43) (числа 19/2 и 7/2 — дробные), то вводится дополнительное ограничение 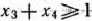 Исключая из него
Исключая из него 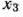 и
и 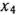 подстановкой вместо них соответствующих значений из уравнений системы ограничений (41), получим
подстановкой вместо них соответствующих значений из уравнений системы ограничений (41), получим 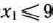 . Этому неравенству соответствует полуплоскость, ограниченная прямой
. Этому неравенству соответствует полуплоскость, ограниченная прямой 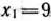 , отсекающей от многоугольника
, отсекающей от многоугольника 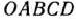 треугольник
треугольник 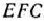 .
.
Как видно из рис. 2.3, областью допустимых решений полученной задачи является многоугольник 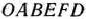 . В точке
. В точке 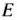 (9; 4) этого многоугольника целевая функция данной задачи принимает максимальное значение. Так как координаты точки
(9; 4) этого многоугольника целевая функция данной задачи принимает максимальное значение. Так как координаты точки 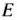 — целые числа и неизвестные
— целые числа и неизвестные 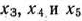 принимают целочисленные значения при подстановке в уравнения (41) значений
принимают целочисленные значения при подстановке в уравнения (41) значений 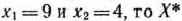 является оптимальным планом задачи (40) —(43). Это следует и из табл. 2.29.
является оптимальным планом задачи (40) —(43). Это следует и из табл. 2.29.
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:

