Оглавление:



Методика решения задач
- Большинство задач статики сводятся к определению реакции связей, в частности реакции различных типов опор. На самом деле наиболее распространены опоры трех типов:а) шарнирно-подвижная опора;б)шарнирно-шарнирная опора;в)неподвижная прижимная опора или жесткое уплотнение. Первые два типа поддержки были рассмотрены в§1.4. В случае жесткого уплотнения исключается любое смещение линейных и угловых балок. В этом случае
последовательность реакций воздействует на герметизированные концы балки со стороны опорной плоскости(рис. 4.6, а) является плоской системой любой силы. Используя теорему о переносе сил, эта система имеет одну силу, равную основному вектору-реакции RB, и точку B относительно основного момента этих сил, равную моменту 4.6, а). Это сочетание силы и пары является связующей
реакцией. Неизвестные модуль и направление реакции RB могут быть Людмила Фирмаль
заменены открытием ее образования RBx и RBy. Поэтому для того, чтобы найти реакцию армирования, необходимо определить две проекции силы R b’r bx и RBy и момента MV(рис. 4.6, а). Символ печати показан на рисунке. 4.6, 6. Все аксиомы и статики справедливы для концентрированной мощности (см.§1.1). На практике часто приходится иметь дело с параллельными силами,
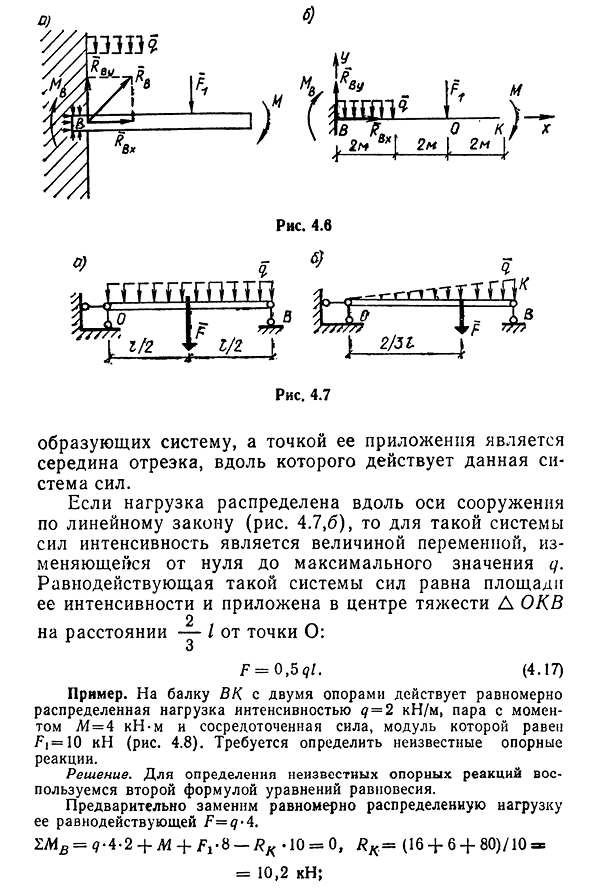
расположенными вдоль данной плоскости по определенному закону. Такая система распределенных сил характеризуется силой q, равной силе на единицу длины нагруженной детали. Интенсивность измеряется в Ньютонах на метр (Н/м). При решении задачи статики система таких сил сначала должна быть заменена результатом. Если нагрузка равномерно распределена по оси конструкции (рис. 4.7, а), в этом случае сила q является постоянной величиной, а F, полученная в результате действия системы таких сил, равна f=ql. (4.16)
- направление силы F совпадает с направлением силы, Ирис 4.6 tFT4-fcff __ £С>< зет P » * flr……. 1, — * * чг1 — Рисунок 4. Семь Образуя систему, точкой ее приложения является середина сегмента, где действует система этой силы. Если нагрузка распределяется по осям конструкции по линейному закону(рис. 4.7, 6), для системы таких сил интенсивность — это величина Переменной, которая изменяется от нуля до максимального значения Q. Результат действия системы таких сил равен площади ее интенсивности и приложен к центру
тяжести D ОКВ на расстоянии-2I1 от точки ОО: F=O, 5ql. (4.17) примеры. Равномерно распределенная сила нагрузки q=2кн / м, крутящий момент L1=4кн * м и концентрация пары, модуль упругости которой равен fi=10кн (рисунок). 4.8). Необходимо определить неизвестную эталонную реакцию. Решение. Вторая формула уравнения равновесия используется для определения неизвестной реакции поддержки. г=^-4 заранее. 2AfB=Q-4-2 + al + F1. 8-РК-10 = 0, = (16 + 6 + 80)/10 ® = 10,2 кн; 43O) EL4L= — F f2+M-g. 4-8+RB
Заменить в результате равномерное распределение нагрузки Людмила Фирмаль
y-10=0, RBy= (20 — 6 + 64)/10= = 7,8 kN;SX = rBx = 0. Из последнего уравнения видно, что балка реакции шарнирной опоры будет равна нулю, если только вертикальная нагрузка действует на горизонтальную составляющую. Для подтверждения правильности найденных реакций воспользуемся уравнением XM= -^. 4-G1+/? ^+/?Л= 0; — 8 — 1 0 + 7 , 8 + 10,2 = 0. Например. В консольной балке БР действует на равномерно распределенную нагрузку силой q-2кн/м, парой крутящих моментов L1=6кнм и концентрацией, коэффициент которой равен а / ==10кн (рис.4.6). Необходимо определить
неизвестную эталонную реакцию. Решение. Чтобы определить неизвестную реакцию, используйте первую форму уравнения равновесия. Два. G= -? — 2 — ^ + ^ = 0, /?B4,=1 4kN;2 / I^ = — <7’25 — GH2 + 6 + /?V^6+MV=0, MV= 20 + 20 — 6 — 84 = — 50 kNm; 2X=/?BX=0. Знак минус указывает на то, что он был указан на диаграмме. 4.6 направление момента реакции противоположно действительному. Для проверки полученной реакции используем формулу ZMQ=RB y-l— 50 — <72*3 + 44 = 0; 56 — 50 — 12 + 6 = 0.
Смотрите также:

