Оглавление:



Методика расчета разветвленных электростатических цепей
Метод расчета разветвленной электростатической цепи. Все методы расчета электрических цепей постоянного тока, описанные в Главе 1, основывались на первом и втором законах Кирхгофа и Ома. Вспомните расовые законы.:
- Первый закон Кирхгофа : = 0 (А. 4. Второй закон Кирхгофа: X Y =£E (A-5) закон Ома / = УГ. (A. Шесть) Аналогичное уравнение справедливо и для электростатического circuit. In фактически, формула (A. 4) альтернативно,
если начальный заряд равен нулю, формула (A. 2) будет выполняться. Людмила Фирмаль
Уравнение(А. 6)вместо уравнения м = УЦ. (A. 6 ’) Формула (A. 5) электростатический контур является общим для электрического n. 。 зет Поэтому существует формальное сходство между электрической и электростатической цепями.
Роль тока I в уравнениях электрических цепей в уравнениях электростатических цепей играет заряд q. роль проводимости g в уравнениях электрических цепей в электростатических цепях играет емкость C.
- Эта формальная аналогия позволяет использовать все методы расчета электрической цепи постоянного тока для расчета электростатической цепи. Только в Формуле для расчета цепи постоянного тока (представленной в первой главе) достаточно заменить ток зарядом, а проводимость g емкостью С.
Наиболее адаптированными к расчету электростатического контура являются метод узлового потенциала и полученный 2-узловой метод. Дело в том, что формулы для расчета этих методов явно включают проводимость (см. формулы 1.20 и 1.22),
поэтому замена проводимости емкости очень проста. Людмила Фирмаль
Если начальный заряд qH отдельных конденсаторов не равен нулю, то влияние этих зарядов на распределение напряжения в цепи рассматривается путем сложения этих зарядов в правой части уравнения метода потенциала перехода (уравнение (1.22)) (см. ток, протекающий от источника к отдельным узлам цепи (см. стр. 34)).
Расчет электрической цепи начинался с выбора положительного направления тока ответвления. Расчет электростатической схемы начинается с того, что выбирается положительное направление приложенного к конденсатору напряжения arbitrarily.
In кроме того, положительное направление напряжения на конденсаторе связано с распределением заряда на пластине, как показано на рисунке 2. Двести четыре、
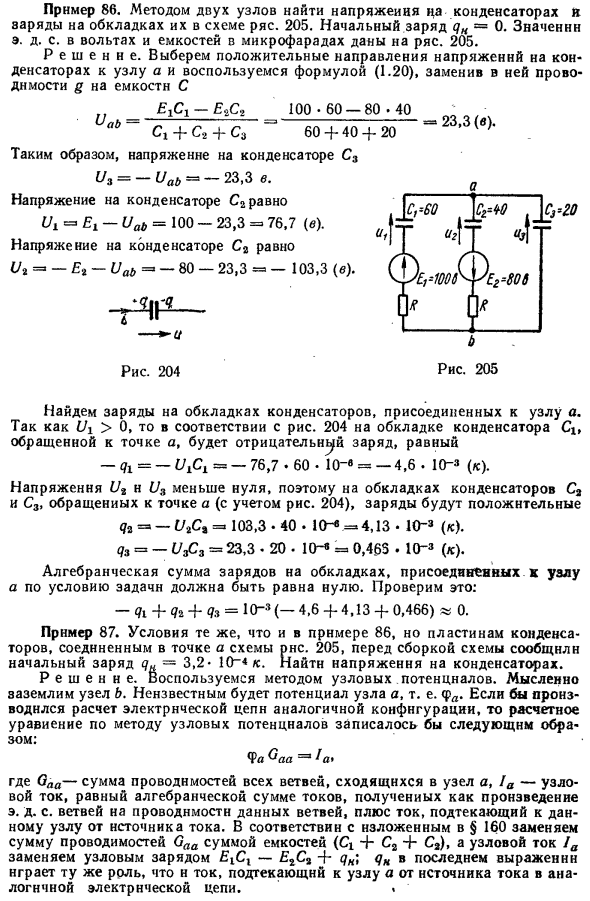
Пример 86. Используя метод 2 узлов, находим напряжение конденсатора Рясной цепи и заряд пластины. 205.Начальный заряд qH =0.величина Э. Д. емкости в s-вольтах и микрофлюидиках обозначается рясой. 205.
Решение. Выберите положительное направление напряжения на конденсаторе до узла а и используйте формулу (1.20) для замены проводимости g в нем на емкость С. Следовательно, напряжение конденсатора С3 = 23,3 дюйма Рисунок 205
Напряжение на конденсаторе С2£4 = и ЗАО = Напряжение на конденсаторе С2 равно Рисунок 204 Найти заряд пластины конденсатора, подключенного к узлу. > От 0, 204 на пластине рисунка конденсатора СХ, обращенной к точке а、
Так как напряжения Ut и U3 меньше нуля, то в пластинах конденсаторов С2 и С3, обращенных к точке а (с учетом рисунка 204), заряд будет положительным. Алгебраическая сумма зарядов на пластинах, Соединенных с узлами, должна быть равна нулю из-за условия задачи.
Пожалуйста, проверьте это: Пример 87.Условия те же, что и в Примере 86, но перед сборкой схемы с конденсаторной пластиной 205, подключенной в точке а схемы, они сообщают начальный заряд= 3,2-10 «<к. найти напряжение на конденсаторе. Решение.
Используйте метод узла potential. It будет заземлять узел b мысленно. Неизвестным является потенциал узла А, или рН. если вычисляется электрическая схема аналогичной конфигурации, то формула расчета по методу потенциала узла описывается следующим образом: ФА Гаа = 4 »
Где Gaa-сумма проводимости всех ветвей, сходящихся на узле, а 1a-ток узла, равный алгебраической сумме тока, полученного как произведение e. d. s В дополнение к проводимости этих ветвей, он разветвляется на ток, протекающий от источника тока к этому узлу.
В соответствии с § 160 соображения, сумма проводимости GAA заменяется суммой емкости (Ci 4 «C2-C3), а ток узла 1a заменяется зарядом узла ElCl-E2Ca 4〜qH.QH последнего уравнения-это ток, который протекает от источника тока в аналогичной электрической цепи к узлу A.」
Получается следующее уравнение: Пха (сі 4 — Ц2 + ЦЗ)= » Етци-E2C2 4-(] «• Заменить цифры: 120•10 » 6 fa = 60 * 10 — < fa = 50 дюймов Напряжение первого конденсатора Уй = экс-ФД = 100-50 = 50©. Напряжение тока 2-ого конденсатора У2 = — Е2-фл = — 80-50 = −130©.
Напряжение 3-го конденсатора — 50 дюймов ’^5 — фа Пример 88. На РНС. 206, а указывает на соединение 3-х контейнеров СрС2 и stars3 звезд. Значение емкости микрофарады записано на рисунке. необходимо найти эквивалентную треугольную значения емкости С12, С13 сад и по возможности РНС. 206, Б, предположение? Начальная стоимость танка равна нулю. Один \ Р
Решение. Принимая во внимание подобие электрических и электростатических цепей (§ 160), воспользуемся формулой (1.28)-(1.30), заменив проводимость их конденсатором:* С23 Пять) CtC2 С, — f-С2+Сз10 * 20 РНС. Двести шесть = гг-3.33 (микро Фарад)’、 С13= 5 микрофарад; С2з-10 люкс.
Смотрите также:

