Оглавление:







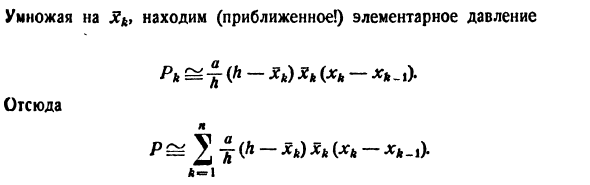

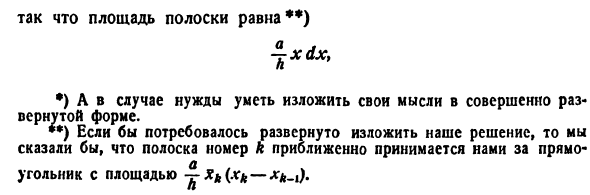




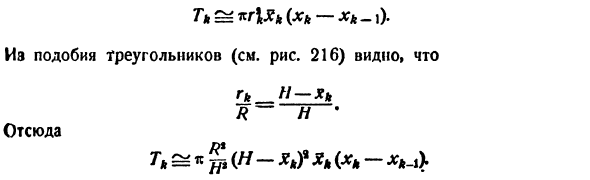





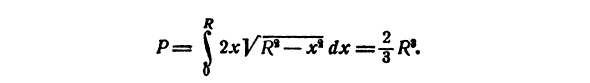
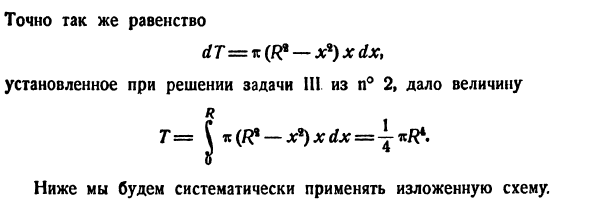

Методика применения определенного интеграла к решению практических задач
Применение конкретных интеграций для решения практических задач n ° 1. Расчет давления жидкости на вертикальных стенках. Рассмотрим несколько задач на одну и ту же тему. I. Возьмите прямоугольный резервуар, наполненный водой перед нами (Рисунок 209). Найти давление *) P на передней стенке резервуара. Напомним некоторые факты из статики. Если под водой есть горизонтальная платформа, давление воды над ней равно весу водяного столба на платформе, то есть в цилиндре на основе этого основания высота погружения равна глубине погружения. — платформа.
- Потому что речь идет о воде, / Удельный вес, равный 1 ■ / —I- / Приведенные выше веса столбцов численно равны T j равняется его объему, т.е. площади участка & / Умножить глубину погружения. } / / U С этой работой, следовательно, \ ч и давление на горизонтальной плоскости Мерси. Рисунок 209. Подводная платформа Невозможно говорить о глубине погружения всего сайта, так как его различные точки находятся на разных глубинах, а не горизонтально. Однако, если сайт очень маленький, все его точки имеют примерно одинаковую глубину. Это почти можно рассматривать как глубину погружения сайта и можно назвать его. Определите давление в такой очень маленькой области.
Для этого представьте, что сайт вращается рядом с одной из своих точек и сайт находится на одном уровне. . С другой стороны, вышеупомянутые правила определения давления уже были применены к новому горизонтальному участку. Поскольку вращение сайта не меняет ни его площади, ни глубины погружения (последнее но Рисунок 209.
Поскольку давление внутри уравновешенной жидкости одинаково в каждой точке во всех направлениях, давление платформы практически не изменится во время показанной операции вращения Людмила Фирмаль
Сайт очень маленький) и тут можно сформулировать Правила. Давление воды на небольшой платформе равно площади этой платформы, умноженной на ее глубину. *) Под давлением понимается вся сила, которую вода толкает к стене, а не сила на единицу площади (т. Е. Общее, а не удельное давление).
Давление на него («основное» давление, обозначенное dP) затем определяется путем умножения этой площади на глубину погружения x полосы. То есть он равен *. дп = ± х * дх. N Получить точную (!) Формулу для всех P здесь Также обратите внимание, что π0 = 0 и xn = h при рассмотрении расширения всего экрана с использованием прямой линии на расстоянии xkt от вершины, чтобы установить пределы интегрирования.
Внутривенно Примените укороченный метод, описанный выше, чтобы найти давление воды P на стороне полукруглого вертикального экрана, диаметр которого совпадает с поверхностью воды (рис. 214). Рисует горизонтальную полосу на щите на глубине х. Сделайте ширину полосы равной **) dx, length /. Из теоремы Пифагора Откуда / = 2Vr * -X \ Так полоса ли 2U7? A-x * dx и его давление dP = 2xVR * -x * dx. \ х Дж | \ Y «s 1 1 \ / 1 1 1 — / -> ■ 1 Рисунок 214.
- Отсюда R — [м ^ — ^ ‘Т- Следующее пытается обобщить вышеупомянутые соображения, но перед этим рассмотрим другую группу проблем. № 2. Найдите работу, которая вам нужна. Откачайте воду из контейнера. I. Налейте воду в цилиндрический бойлер (рис. 215) и откачайте воду с помощью насоса. Вам нужно найти работу, необходимую для этого. Во-первых, определите работу, которую нужно провести, чтобы удалить одну частицу воды из котла.
Эта частица должна быть поднята до конца котла% I и уже будет вытекать из котла под действием веса (движение частиц вдоль горизонтального участка шланга насоса не происходит). Поэтому необходимо только преодолеть гравитацию частиц с вертикальным поперечным сечением пути, равным глубине погружения частиц. Требуемая для этого работа равна произведению указанных выше количеств. Поскольку удельный вес воды = 1, вес частицы равен ее объему.
Следовательно, работа, необходимая для удаления частиц воды из котла, равна объему частиц и является тонкой в глубине погружения. Вы не можете применять это правило напрямую для решения проблемы. Потому что разные частицы находятся на разных глубинах. Действуйте так же, как при l ° 1. Это значит R p = J 2xVrRr ^ J? дх = -о Это Одна плоскость, параллельная нижней части свинцового n-цилиндра и глубокая . В результате этих действий общая масса воды разбивается на n цилиндрических «базовых * слоев». Если ранг X является измельчением сегментов [O, I],
Также установите jc0 = 0, xn = N для однородности Людмила Фирмаль
То есть максимальная разница xk-Xk-v очень мала, высота всех слоев мала, и вы можете приблизительно догадаться, что все частицы находятся на одной и той же глубине в одном слое. Для этого номера слоя глубины k (выше) используйте число Jck, произвольно выбранное между xk_t и xk. Работа, необходимая для откачки этого слоя — это объем (xk-jca_j), умноженный на Xk. Получить приближенные уравнения для всех найденных работ T 1 Отсюда вы можете получить более точный X, например, n ° 1. N T = j nR * x dx = ±. «R * H *. II. Теперь у вас есть работа, необходимая для прокачки конической воронки (Рисунок 216).
Используя тот же метод, поместите всю горизонтальную плоскость вглубь и поразите всю воду воды Рисунок 216. T N IV хку найти- * 0 = 0 << … <xn_t <= I, n слоев. Каждый из этих слоев (конических усечений) считается цилиндром, который не влияет на конечный результат. Ошибка в определении объема слоя состоит в том, что он становится равным X- * 0, что бесконечно меньше самого объема.
Пусть радиус слоя представлен rk числом k (пронумерованным сверху вниз), и предположим, что слой находится на глубине Xk. Здесь работа по удалению слоя с номером k Тк ^ кг \ Хк (хк-хк-1). Исходя из сходства треугольников (см. Рис. 216), rk_N-xk R AND Отсюда Hk? Hk (hk-hk_ $
так r ^ 2 «§ (I — ** (** — * k-i)> 1 С пределом X- * 0 вы найдете точное значение G N T = [njp (H-x) * xdx = j2 * R * H *. III. Вы можете найти работу для откачки воды из полушария (Рисунок 217). Упростить все решение и опустить эти детали Мы уже ^ _ ^ _ ^ Я знаю, не влияет на конец -I_I Конечный результат. Это означает, что весь //} Представленный том будет разобран- / Рассмотрим базовый слой с толщиной dx и толщиной x.
Если рассматривать цилиндр с радиусом r, то работа, которая сжимает этот слой (элемент * work, обозначенный dT), равна произведению. (Nr * dx) x = nr * xdx.
Из теоремы Пифагора (рис. 217) r * = R? -х \ итак dT = n (R! * -x *) xdx, Откуда R T = ^ KiRi-x ^ xdx ^^ R1. Внутривенно Вы можете найти работу для откачки воды из желоба в форме полуцилиндра (Рисунок 218). Слой, расположенный на глубине x и толщине dx, будет прямоугольной плиткой. она Длина равна всей длине впадины H, а ширина / определяется из теоремы Пифагора / = 21 //? -А Высота слоя dx. То есть его объем равен HIх = 2НУВ? -x * dx и основные задачи dT = 2Hx VR * -x * dx. Отсюда R _ T = [2HxVR * -Mx = 4tf /? J 3 № 3. Правила, которые применяют интеграцию к конкретным вопросам.
Он пытается охватить опыт, полученный в предыдущих двух параграфах, с конкретной общей схемой. Значение физической или геометрической величины A, соответствующее изменению переменной x от a до b (например, значение давления воды в вертикальной стенке P, соответствующее изменению глубины x от 0 до //) Предположим, вы хотите найти. Предположим, что это количество является аддитивным. То есть, когда интервал [a, b] делится на точку c, a <c <C ^ b соответствует частям [a, c] и [cf b], значению A и всему сегменту [a, b ] Равно сумме значений, соответствующих [a, c] и [c, b \ *).
Перейдите к решению проблемы и разбейте отрезок [a, b] на n частей с помощью точки. xb = a <xx <… <xn_x = b. (2) В соответствии с этим значение A интереса делится на n слагаемых Alf As, An. А = 2 А-ч. Предположим, что существует функция / (*), в которой базовый член Ak, соответствующий интервалу [xb_r, xk] *, можно записать в виде Ak ^ f (Xb) {xk-xk_x)> (3) Здесь Xk находится между xki xk, а погрешность (3) уравнения ранга X (2), бесконечно малого для шлифования, бесконечно меньше, чем Ak.
В этом случае приближенное выражение A получается. Я Л / () ( Точнее, Х меньше. В результате точное значение A действует как X-> 0 или совпадает с записанным общим пределом. (4) б но На практике этот аргумент представлен в более короткой форме с элементом A размера A, соответствующим базовому сегменту [x, jc-J-Ajc], вплоть до небольшого сегмента более высокого порядка * (5) (6) И говорят, что величина A получается суммированием элементов dA .
Фактически, интеграл является его пределом, а не просто суммой, и благодаря этому переходу предела результат является точным, а не приблизительным. Следовательно, целое найдет функцию f (удовлетворяющую x \ соотношению (6)). Например, давайте вернемся к n ° 1 Задача IV. dP = 2xVR * -x * dxt И это привело нас к церемонии Точность этого правила приближения увеличивается с размером сайта *).
Давайте вернемся к задаче. Вышеуказанные правила не применяются, потому что передняя стенка резервуара не такая маленькая. Чтобы сделать его еще применимым, возьмите очень большое число n и нарисуйте горизонтальную линию, разделенную расстоянием xx <[x% <… <xn_ от верхнего края вдоль передней стенки n-1 резервуара (Рис. 210). Для равномерного обозначения x0—0 и xn = h. Наша прямая линия разделяет стену \ А-г но тсссххххххххх ку по узким полоскам. Полоса с номером k (пронумерована сверху вниз) заштрихована на чертеже. Максимальная разница * k-X \ — \ (т. Е. Если генерируется ранг X- * Сегмент [0, Л] маленький, каждая полоска очень узкая, все Все точки находятся примерно на одной глубине. Поэтому давление одной полосы можно рассчитать в соответствии с приведенными выше правилами **).
Площадь номера полосы k равна основанию a, умноженному на высоту xk-jr ^ j. Другими словами, эта область равна (xb-xk_x). Xk для глубины погружения полосы. Может принимать любое число от \ (глубина вверху полосы) до xk (глубина внизу). Фактически, в конце концов, понятие глубины погружения самой полосы было определено только как глубина погружения одной из точек. Выберите Xk, удовлетворяющее двойному неравенству Xk <xkt х, б Используйте этот Xk для глубины погружения полосы номер k.
Далее, давление этой полосы («основное * давление») представляется (приблизительно!) Общее давление Р составляет (почти):Одинаково равный dT = i: {P? -X *) x dx> n ° 2 установлено при решении задачи III и дает значение G 1 T = \ it (R * -xt) xdx = ± R Ri Далее приведенная выше схема применяется систематически.
о) •) Это означает, что относительная ошибка из-за применения правила, как правило, равна нулю с размерами сайта. **) На самом деле, как правило, было важно, чтобы операция поворота сайта не меняла глубину погружения отдельных точек сайта очень мало. Таким образом, вы можете применить правило к полосе, но из-за ее длины полоса не является «маленькой».
Точность уравнения (1) увеличивается с уменьшением X. Следовательно, точное значение P равно его пределу, а не сумме, указанной выше. N /> = Hm 2 aXK (xk-xkL x-OdG » Но этот предел как общий предел формы N 2 / C **) (hk-hk _ |) Есть определенный интеграл. так L P = \ axdx. о Дальнейшие расчеты не сложны: I. Рассмотрим еще одну проблему того же типа. Пусть дно треугольника упадет вертикально в воду с треугольной оболочкой. Уровень свободной поверхности II I _ вода (рис. 211).
Необходимо решить 1 \ / г? Давление воды P на одной стороне экрана. \ / & L-7, чтобы применить тот же метод h tgzzzzzzzzzzJz ~ -zJL или более «снова, используйте горизонтальный, чтобы разделить экран на очень узкие полосы VJ \ / Линия расстояния \ J = 0 <Oi <••• <■ * / »-! Оя = L С вершины щита. Снова на полосе. 211. Номер k для применения вышеуказанного Как правило, рассмотрим число Xk, произвольно выбранное между xk, i, xk, с учетом глубины погружения этой полосы. Осталось найти участок полосы. Эта полоса трапециевидная.
Но (Внимание!) Из-за того, что полоса очень узкая, ее можно принять за прямоугольник с высокой точностью. вхождение (Относительная!) Ошибка, возникающая при определении площади полосы, становится меньше по мере сужения полосы. Из предыдущего примера мы уже знаем, что ширина полосы должна уменьшаться бесконечно. Поэтому ошибки не влияют на конечный результат *), и расчет упрощается. здесь •) Если каждый член определенной суммы найден с очень небольшой относительной ошибкой, общая относительная ошибка также очень мала.
Мы сталкиваемся с очень общей природой. Это всегда относится к решению самых разнообразных задач интегральных вычислений: при вычислении элементарных терминов обращайте внимание главным образом на простоту их представления и игнорируйте некоторые из этих терминов при необходимости вы.
По сравнению с тем, что считается. Сам базовый термин, который занимает нас в X 0, имеет тенденцию быть нулевым, поэтому идея выражается в том, когда вы находите определенный ^ a ^ Возможна интеграция, интеграция Игнорировать все бесконечные T // £ Бесконечное подмножество этой суммы m- [\ ^ / По существу бесконечные части | \ * / _ 1 Более высокий порядок, чем собственная терминология V J. , \ / Когда вы вернетесь к задаче, номер полосы k длина (т. е. прямой I \ J Квадрат, который заменяет полосу), принимает длину любого горизонтального отрезка. 212. Общая линия, проведенная вдоль полосы. Самое простое и естественное — использовать прямую линию на расстоянии Xb. Эта прямая линия используется как глубина погружения полосы.
Из сходства треугольника, показанного на фигуре 212, ясно, что длина полосы удовлетворяет соотношению а-л » / * h-Xk Откуда 4 = 4 Поскольку ширина полосы равна разности xk-xk_it, ее площадь ^ (H-Xb) {xk-xk_t).Вы хотите умножить на j? * Мы (приблизительно!) Я p = 2 т (L «» * * k -XK B * = 1
Точное значение P — это общее ограничение по X L О, это \ P = \ ± (h-x) xdx. ах1 6 в конце концов н я Г. х * хр * III. Вот еще один пример аналогичной проблемы, решаемой с использованием опыта, уже накопленного в решении задач I и II. Опустите вертикальный экран треугольника в воду так, чтобы дно треугольника было параллельно свободной поверхности воды. И противоположный пик в GG этой поверхности (рис. 213) Найти давление I / \ p на одной стороне щита. Я / х решаю эту проблему таким же образом Я, как и прежде, дома.
Итак, мы первые ifazzzzzzzzzzzzb ^ iiZLdx P представляет приблизительно сумму, и точное значение f \ ** r-i-> • \ P равно пределу этой суммы- / _ \ we, т.е. интегралу. | Рассчитать любое давление _ _ I ^ Сделай сок и положи на него щит. 213. Введите глубину погружения полосы Xk. Но мы Мы уже знаем, что символы просто заменяются на x при переходе от суммы к интегралу. Аналогично, этот переход заменяет ширину полосы xk-xl символом dx. Учитывая все это, можно легко сказать, что горизонтальная полоса с экраном глубиной х и шириной дхм (рис. 213).
Фраза, написанная в кавычках, является просто сокращением для мыслительной последовательности, подробно описанной в примерах I и I. Чтобы научиться вычислять интегралы, вам нужно выучить аналогичный сокращенный метод речи *). Длина I основной полосы похожа на треугольник. ч ‘Площадь полосы **) ± xdx, •) При необходимости сможете выразить свои мысли в полностью расширенном формате. • *) Если нам нужно объяснить наше решение, мы можем сказать, что номер полосы k приблизительно взят непосредственно нами. но Площадь с площадью у
Смотрите также:

