Оглавление:
Метод замены переменных
Этот распространённый метод используется для разных целей: упрощение задачи и повышение её наглядности, придание уравнению (неравенству, системе и проч.) более симметричного вида, сведение одного уравнения к системе нескольких уравнений, рационализация иррациональностей (см. пункт 3.3) и т.д. Иными словами, введение новых переменных производится в тех случаях, когда есть возможность свести задачу к другой, для которой существует более эффективный способ решения.
Существуют виды уравнений, для которых разработаны специальные подстановки, позволяющие наиболее оптимально решать эти уравнения (например, симметрические и возвратные уравнения, однородные уравнения и многие другие). Рассмотрим дополнительно группу примеров, иллюстрирующих различные цели использования этого подхода.
Начнём с примера, в котором при помощи замены неизвестной рациональное неравенство сводится также к рациональному, но более простому алгебраическому неравенству.
Пример №350.
Решить неравенство
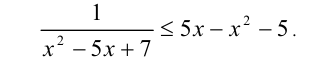
Решение:
Положим 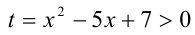 . Тогда необходимо решить неравенство
. Тогда необходимо решить неравенство 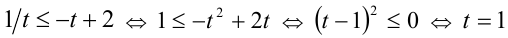 . Выполнив обратную подстановку, получим квадратное уравнение
. Выполнив обратную подстановку, получим квадратное уравнение 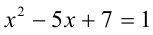 , решив которое, приходим к ответу. Ответ:
, решив которое, приходим к ответу. Ответ: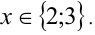
В следующем примере дробно-рациональное уравнение заменой сводится к целому алгебраическому уравнению.
Пример №351.
Решить уравнение 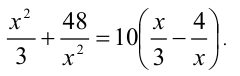
Решение:
Обозначим разность 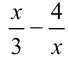 через
через 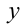 , тогда уравнение перепишется в виде
, тогда уравнение перепишется в виде 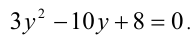 Это уравнение имеет два корня
Это уравнение имеет два корня 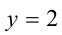 и
и 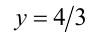 , что приводит к совокупности уравнений
, что приводит к совокупности уравнений
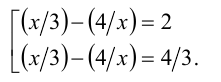
Первое уравнение даёт корни 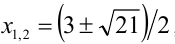 , а второе —
, а второе — 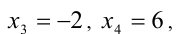 которые и будут решениями исходного уравнения.
которые и будут решениями исходного уравнения.
В некоторых случаях алгебраическую задачу (даже если в её условиях не содержится радикалов) с помощью специальных тригонометрических подстановок бывает целесообразно свести к тригонометрической задаче, и далее уже решать её методами тригонометрии.
Пример №352.
Известно, что 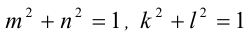 и
и 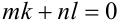 . Чему равно значение
. Чему равно значение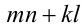 ?
?
Решение:
Воспользуемся тем, что если два действительных числа X, у удовлетворяют равенству

где 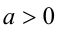 — заданное число, то
— заданное число, то 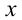 и
и 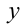 можно представить в тригонометрическом виде
можно представить в тригонометрическом виде 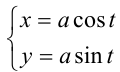 , где
, где 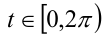 . В самом деле, уравнение (1) задаёт на плоскости
. В самом деле, уравнение (1) задаёт на плоскости 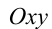 окружность радиуса
окружность радиуса 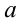 с центром в начале координат. При изменении
с центром в начале координат. При изменении 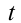 от
от 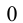 до
до 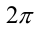 точка с координатами
точка с координатами 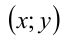 ровно один раз обходит окружность, и таким образом между точками окружности и полуинтервалом
ровно один раз обходит окружность, и таким образом между точками окружности и полуинтервалом 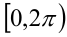 оказывается установлено взаимно однозначное соответствие. Это означает, что каждому значению
оказывается установлено взаимно однозначное соответствие. Это означает, что каждому значению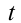 из
из 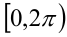 соответствует единственная пара чисел
соответствует единственная пара чисел 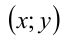 , удовлетворяющих равенству (1), и наоборот, каждой паре чисел, удовлетворяющих (1), соответствует единственное значение
, удовлетворяющих равенству (1), и наоборот, каждой паре чисел, удовлетворяющих (1), соответствует единственное значение 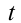 из
из 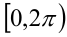 .
.
Итак, поскольку числа 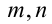 удовлетворяют равенству
удовлетворяют равенству 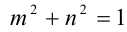 , то найдётся такое число
, то найдётся такое число 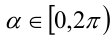 , что
, что 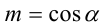 ,
, 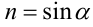 . Аналогично, поскольку числа
. Аналогично, поскольку числа 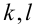 удовлетворяют равенству
удовлетворяют равенству 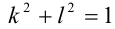 , то найдётся такое число
, то найдётся такое число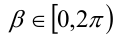 , что
, что 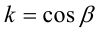 ,
, 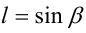 . При этом условие
. При этом условие 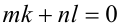 примет вид
примет вид
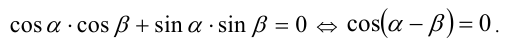
Выполнив тригонометрическую подстановку в искомом выражении 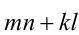 , получим:
, получим:
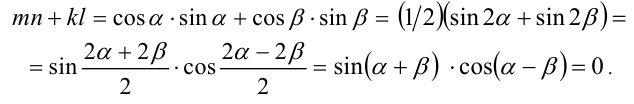
Введение новых переменных может быть вызвано необходимостью понизить степень уравнения, упростив при этом решение задачи.
Пример №353.
Решить уравнение 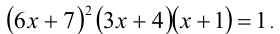
Решение:
Сведём данное уравнение 4-й степени к квадратному уравнению. Для этого вначале умножим обе части уравнения на 12 и приведём его к виду
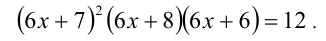
Затем сделаем подстановку 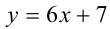 , что приведёт к уравнению
, что приведёт к уравнению
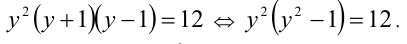
Сделав ещё одну подстановку 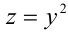 , сведём окончательно данное биквадратное уравнение к квадратному уравнению
, сведём окончательно данное биквадратное уравнение к квадратному уравнению 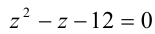 , решив которое, находим корни
, решив которое, находим корни 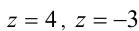 . Тогда
. Тогда 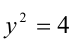 и
и 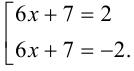
Ответ: 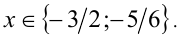
В следующем примере используется симметризирующая подстановка. Название говорит само за себя: уравнению придаётся более «симметричный» вид. Новая переменная является средним арифметическим входящих в уравнение выражений. При её применении уравнение 4-й степени общего вида приводится к более простому частному случаю, а именно, симметризация уравнения позволяет «убрать» из уравнения нечётные степени неизвестной, оставив только чётные и превратив его, таким образом, в биквадратное уравнение.
Пример №354.
Решить уравнение
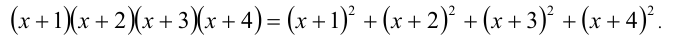
Решение:
Выполним симметризирующую подстановку
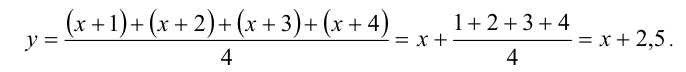
Тогда уравнение примет вид
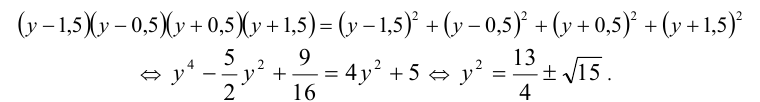
Ответ: 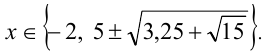
6.Близко к методу введения новых переменных стоит так называемый метод введения параметра. Не всегда введение параметра усложняет задачу. На примере, рассмотренном ниже, видно, как включение параметра в уравнение вместо числового коэффициента позволяет лучше «разглядеть» способ дальнейшего его решения — рассмотрение уравнения как квадратного относительно введённой величины.
Пример №355.
Решить уравнение
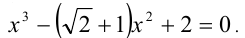
Решение:
Введём в уравнение параметр, положив 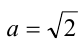 :
:
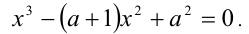
Рассмотрим теперь это уравнение как квадратное относительно 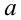 . Приведём его к стандартному виду
. Приведём его к стандартному виду 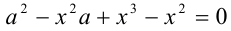 и вычислим дискриминант
и вычислим дискриминант 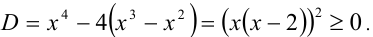 Найдём корни:
Найдём корни:
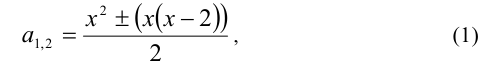
т.е. 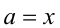 или
или 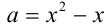 . Параметр к этому моменту сыграл свою положительную роль, позволив свести решение кубического относительно
. Параметр к этому моменту сыграл свою положительную роль, позволив свести решение кубического относительно 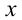 уравнения к совокупности двух уравнений более низкой степени: квадратного и линейного.
уравнения к совокупности двух уравнений более низкой степени: квадратного и линейного.
Заменяя 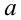 числом
числом 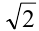 , получим совокупность
, получим совокупность
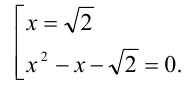
Отсюда находим решения: 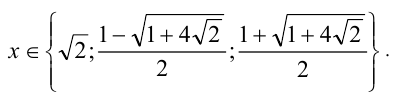
Замечание. В формуле корней квадратного уравнения более корректным было, вообще говоря, написать

Однако когда ищутся оба корня, то использование формул (1) и (2) приводит к одному результату. Именно поэтому часто в подобных ситуациях модуль опускают.
7.Отметим, что, вообще говоря, не всегда в задаче нужно полностью переходить к новым переменным. Иногда имеет смысл, вводя новую переменную, сохранить в задаче и первоначальную переменную, т.е. сделать частичную замену переменных. Так, сведением к системе уравнений, решаются некоторые уравнения. Рассмотрим в качестве пояснения пример.
Пример №356.
Решить уравнение
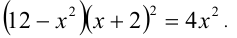
Решение:
Так как 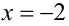 не является корнем, то уравнение можно привести к равносильному виду
не является корнем, то уравнение можно привести к равносильному виду
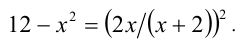
Положим 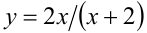 , тогда уравнение сведётся к равносильной ему системе
, тогда уравнение сведётся к равносильной ему системе
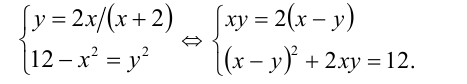
Решая эту систему относительно 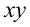 и
и 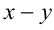 , приходим к ответу:
, приходим к ответу: 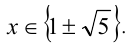
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

