Оглавление:
Метод замены неизвестных с применением модуля
Суть метода состоит в том, что в целях упрощения дальнейшего решения задачи вводится одна или несколько новых переменных. В конце решения задачи делается так называемая обратная подстановка, в результате которой осуществляется переход к первоначальным переменным. Возможные трудности при использовании этого метода связаны с необходимостью подбора удачной подстановки, которую не всегда бывает легко увидеть. Рассмотрим примеры использования этого подхода в задачах с модулями.
Пример №318.
Решить неравенство 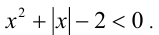
Решение:
Положим 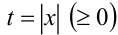 , тогда имеем квадратное неравенство
, тогда имеем квадратное неравенство 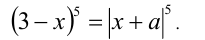 (так как
(так как 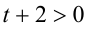 ). Итак,
). Итак, 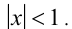 Ответ:
Ответ: 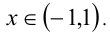
Пример №319.
Решить неравенство
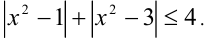
Решение:
Положим 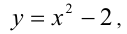 тогда неравенство примет вид
тогда неравенство примет вид 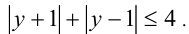 Решим его с помощью метода интервалов.
Решим его с помощью метода интервалов.
1) 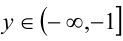 : раскрыв модули на этом промежутке, получим
: раскрыв модули на этом промежутке, получим 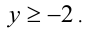 Пересекая с промежутком, находим решения
Пересекая с промежутком, находим решения 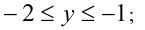
2)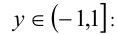 раскрывая оба модуля, получим
раскрывая оба модуля, получим 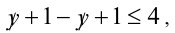 т.е.
т.е. 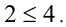 Это неравенство выполняется при всех у из рассматриваемого полуинтервала, поэтому имеем решения
Это неравенство выполняется при всех у из рассматриваемого полуинтервала, поэтому имеем решения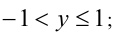
3) 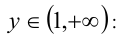 на этом интервале неравенство приводится к виду
на этом интервале неравенство приводится к виду 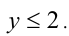 Пересекая с промежутком, получим
Пересекая с промежутком, получим 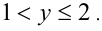
Объединяя все найденные решения, получаем 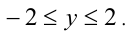 Оста-лось сделать обратную подстановку:
Оста-лось сделать обратную подстановку: 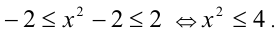 Отсюда получаем окончательный ответ. Ответ:
Отсюда получаем окончательный ответ. Ответ: 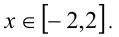
Пример №320.
Решить уравнение
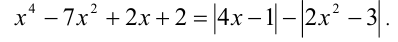
Решение:
Выполним двойную подстановку: 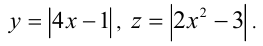 Так как
Так как 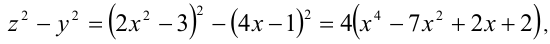 то исходное уравнение в результате замены примет вид:
то исходное уравнение в результате замены примет вид: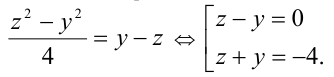 Первое из уравнений сводится в результате обратной подстановки к уравнению
Первое из уравнений сводится в результате обратной подстановки к уравнению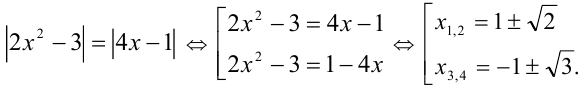
Второе из уравнений 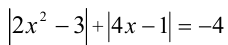 не имеет решений. Ответ:
не имеет решений. Ответ: 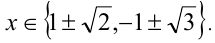
Пример №321.
Решить уравнение
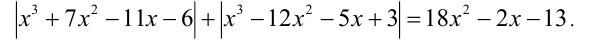
Решение:
Положим 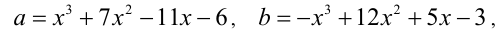 Тогда уравнение примет вид
Тогда уравнение примет вид
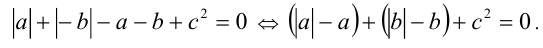
Поскольку все три слагаемых в левой части уравнения неотрицательны, то уравнение равносильно системе
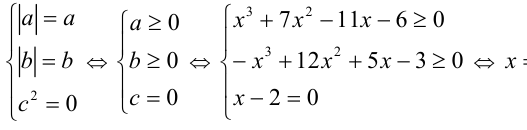
Пример №322.
Числа a,b,c,d удовлетворяют условиям 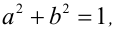
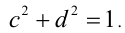 Доказать, что
Доказать, что 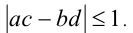
Решение:
Воспользуемся тригонометрической подстановкой. Из условий задачи следует, что 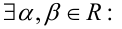
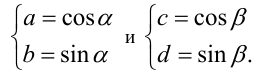
Подставляя в неравенство, получим
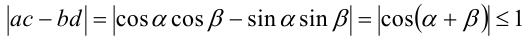 — верно, что и требовалось доказать.
— верно, что и требовалось доказать.
Другие примеры на замену переменной были рассмотрены выше в пункте, посвященном использованию свойств модулей.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

