Оглавление:
Метод замены множителей на множители равных знаков
При использовании обобщённого метода интервалов для решения неравенств полезным может оказаться следующий подход, называемый в данной книге методом замены множителей на множители равных знаков. Некоторые авторы, например, Дорофеев Г.В., относят этот метод к разновидности обобщённого метода интервалов, а другие, скажем, Моденов В.П., называют методом логических схем равносильных высказываний. Рассмотрим суть этого подхода.
Пусть, например, решается неравенство вида
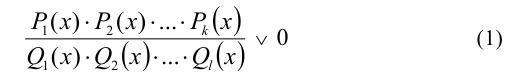
(количество сомножителей 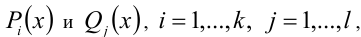 в числителе
в числителе
и знаменателе дроби, а также знак неравенства могут быть произвольными). Пусть для одного из сомножителей (ради определённости будем считать, что это
сомножитель 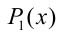 ) нашлась такая функция
) нашлась такая функция 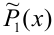 , определённая на ОДЗ неравенства, что она обращается в нуль одновременно с
, определённая на ОДЗ неравенства, что она обращается в нуль одновременно с 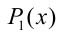 , а при остальных x из ОДЗ имеет тот же знак, что и
, а при остальных x из ОДЗ имеет тот же знак, что и 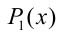 . В остальном, вообще говоря, функция
. В остальном, вообще говоря, функция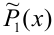 может иметь любой вид. Тогда исходное неравенство равносильно на ОДЗ неравенству
может иметь любой вид. Тогда исходное неравенство равносильно на ОДЗ неравенству
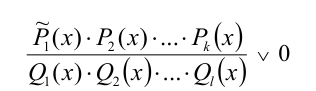
(сомножитель 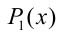 заменили сомножителем
заменили сомножителем 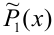 того же знака). Приведём наиболее типичные примеры использования этого подхода.
того же знака). Приведём наиболее типичные примеры использования этого подхода.
1) Если в неравенство (1) входит множитель 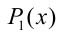 вида
вида 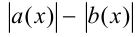 , то его можно заменить в целях упрощения решения задачи на множитель
, то его можно заменить в целях упрощения решения задачи на множитель 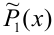 вида
вида 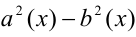 , не содержащий модулей, так как
, не содержащий модулей, так как 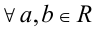 знаки выражений
знаки выражений 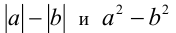 совпадают (обращаются в нуль они также одновременно).
совпадают (обращаются в нуль они также одновременно).
2) Множитель 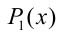 логарифмического вида
логарифмического вида 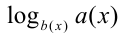 на ОДЗ задачи заменяют эквивалентным ему по знаку, но более простым множителем
на ОДЗ задачи заменяют эквивалентным ему по знаку, но более простым множителем 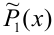 нелогарифмического вида
нелогарифмического вида 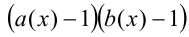 . Множитель
. Множитель 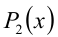 в виде разности двух логарифмов по одному основанию
в виде разности двух логарифмов по одному основанию 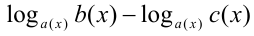 заменяют на ОДЗ (т.е. при дополнительном условии
заменяют на ОДЗ (т.е. при дополнительном условии 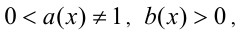
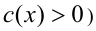 произведением вида
произведением вида 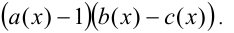
Поскольку в результате применения этого метода трансцендентное неравенство (логарифмическое, показательное и т.д.) часто приводится к рациональному виду, то его в этих случаях относят к методам рационализации.
Пример №215.
Решить неравенство
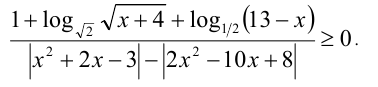
Решение:
Входящие в данное неравенство логарифмы определены при 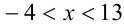 . Преобразуем числитель дроби
. Преобразуем числитель дроби
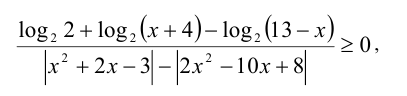
или
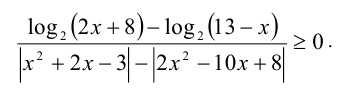
Теперь, помня об ограничении 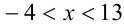 , заменим и числитель, и знаменатель на более простые выражения алгебраического вида (эквивалентного знака), перейдя к равносильному неравенству
, заменим и числитель, и знаменатель на более простые выражения алгебраического вида (эквивалентного знака), перейдя к равносильному неравенству
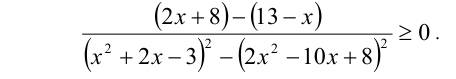
Разложив знаменатель на множители и упростив, приходим к неравенству
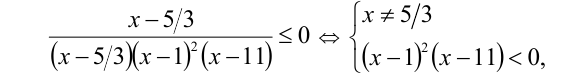
откуда с учётом ОДЗ находим ответ: 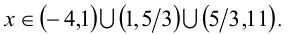
3) Множитель показательно-степенного вида 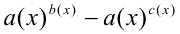 на ОДЗ неравенства (т.е. при дополнительном условии
на ОДЗ неравенства (т.е. при дополнительном условии 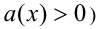 также заменяют произведением
также заменяют произведением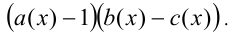
Пример №216.
Решить неравенство
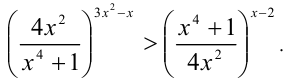
Решение:
Приведём неравенство к виду
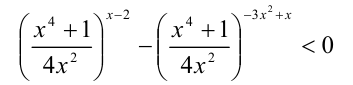
и, применяя указанный выше приём, перейдём к эквивалентному ему дробно-рациональному алгебраическому неравенству:
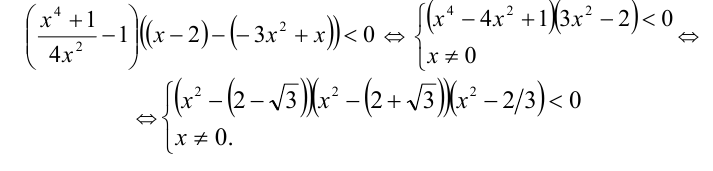

Ответ:
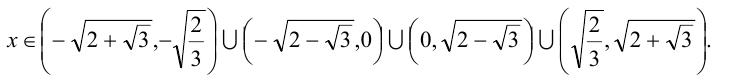
4) Множитель вида 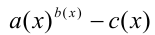 можно заменить при условии
можно заменить при условии 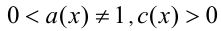 множителем
множителем 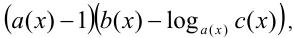 а множитель вида
а множитель вида 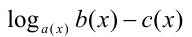 соответственно множителем
соответственно множителем 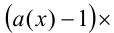
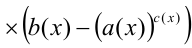 (при условии
(при условии 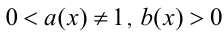 ).
).
5) Множитель иррационального вида 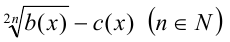 заменяют при условии
заменяют при условии 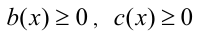 рациональным выражением
рациональным выражением 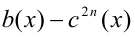 , а множитель вида
, а множитель вида 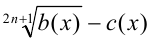 при любых
при любых 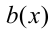 и
и 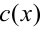 соответственно разностью
соответственно разностью 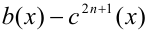 и так далее.
и так далее.
Пример №217.
Решить неравенство
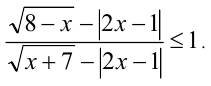
Решение:
ОДЗ: 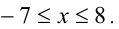 Выполним равносильные преобразования:
Выполним равносильные преобразования:
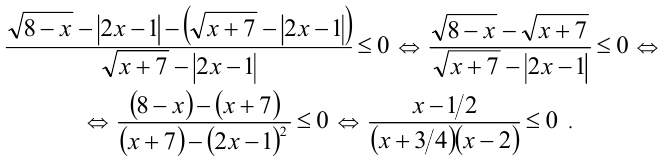
С учётом ОДЗ приходим к ответу: 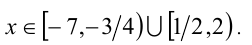
Применение этого метода на практике часто позволяет существенно упростить решение неравенства и сэкономить время. Важно лишь отслеживать равносильность этих переходов.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

