Метод взвешенных сумм с точечным оцениванием весов
Метод заключается в следующем. Каждый критерий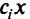 
умножается на положительный скалярный «вес» 
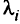все 
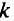взвешенных критериев суммируются и образуют составную целевую функцию (целевую функцию из взвешенной суммы) 
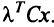. Предположим, что все весовые векторы 
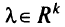нормированы так, что сумма их координат 
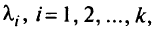равна I (т.е. в соответствии с нормой 
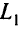). Множество таких весовых векторов имеет вид
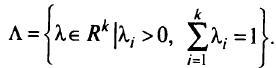
При известных весовых векторах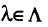 
получаем однокритериальную задачу ЛП
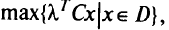
которая будет иметь оптимальное или достаточно близкое к нему решение для неизвестной нам функции полезности.
Основная трудность заключается в отыскании подходящего весового вектора. В ряде случаев веса выбирают пропорционально важности критериев или применяют метод взвешенных сумм, если считать его способом ранжирования точек из допустимого множества в соответствии с их коэффициентом качества, под которым понимают значение составной критериальной функции.
Теорема 1. Точка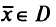 
, которая максимизирует взвешенные суммы в задаче ЛП
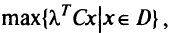
где 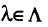является эффективной точкой.
Теорема 2. Если 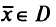— эффективная точка, то существует вектор 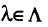, когда 
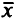— решение задачи
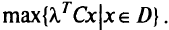
В силу этих теорем все точки,максимизирующие при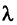 
> 0 взве-шенные суммы в задаче ЛП, являются эффективными. Если взвешенная сумма в задаче ЛП оказалась неограниченной для некоторого весового вектора, то последнему нельзя поставить в соответствие ни одной эффективной точки, но могут существовать другие положительные весовые векторы, для которых взвешенные суммы будут ограничены.
Если один или более весов — нули, то нельзя гарантировать, что все точки, максимизирующие взвешенную сумму в задаче ЛП являются эффективными. Следует помнить, что стандартные пакеты ЛП могут не выявлять все крайние точки, максимизирующие целевую функцию, а выдают лишь первую подходящую точку, даже если эта точка не является эффективной.
Один из способов задать веса — назначить разным критериям веса так, чтобы градиент взвешенной суммы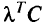 
совпадал по направлению с градиентом функции полезности
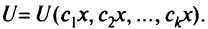
Пусть функция полезности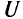 
дифференцируема. Градиент сложной функции 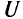в точке 
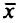имеет вид
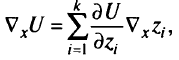
где
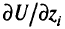
вычисляются в точке
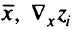
градиент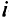 
-го критерия:
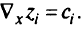
Полагая, что
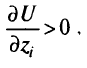
введем положительный скаляр
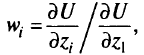
вычисленный в точке 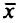. Тогда направление градиента 
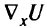в точке 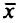можно задать в виде
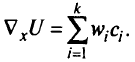
Нормируя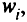 
получим
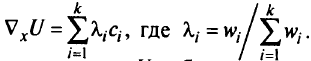
Функция полезности 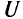в общем случае нелинейна, и ее градиент будет изменяться от точки к точке. Рассмотрим касательную гиперплоскость к поверхности уровня функции 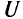в точке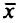
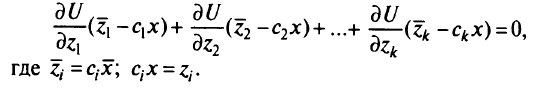
Разделив это уравнение на
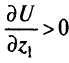
получим
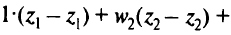
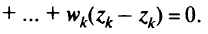
Для оценки
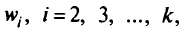
введем произвольную величину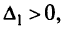 
, чтобы скомпенсировать изменения градиента, и в качестве оценки 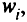, выберем величину 
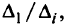, вычисленную в точке 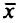. При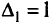 
получим
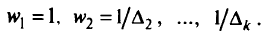
Нормируя оценки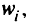 
находим 
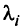. От этого метода оценки весов не следует ожидать большой точности.
В общем случае множество оптимальных весовых векторов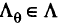 
(т.е. при некотором 
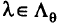есть точка, являющаяся решением
составной задачи ЛП
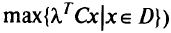
зависит не только от предпочтений ЛПР, но и от соотношения длин векторов-градиентов целевых функций и геометрии допустимой области, а также от степени корреляции критериев (от величины угла между градиентами целевых функций — чем меньше этот угол, тем больше корреляция между критериями). При сильной корреляции двух критериев, задав большой вес одному критерию, нет необходимости вводить какой-либо вес для другого критерия. При увеличении размерности задачи трудности оценки оптимальных весовых векторов возрастают.
Для облегчения процедуры отыскания оптимальных весовых векторов и решения задач МКЛП проводится масштабирование целевых функций путем применения множителей, выравнивающих диапазоны изменения критериев, и выбора наиболее подходящего определения нормы.
Эта теория взята со страницы лекций по предмету «математическое программирование»:
Предмет математическое программирование
Возможно эти страницы вам будут полезны:
| Метод проекции градиента |
| Многокритериальные задачи линейного программирования |
| Сжатие множества допустимых решений |
| Минимальные значения критериев на множестве эффективных точек |
