Метод стэм для задачи принятия решений - Динамическое программирование

Оглавление:

Теория принятия решений — это набор методов и моделей, используемых для обоснования решений. Теория решений — это совокупность методов и моделей, используемых для обоснования решений на этапах анализа, разработки и эксплуатации сложных систем различного типа: Информационные, технические, производственные, организационные и экономические системы и др.

Человек наделен сознанием, будучи свободным и обреченным принимать решения и стараться делать все наилучшим образом. В самом общем смысле, теория оптимального принятия решений — это совокупность математических и численных методов, которые направлены на поиск наилучших вариантов из набора альтернатив и избежание их полного поиска. Учитывая тот факт, что размерность практических задач, как правило, достаточно велика и вычисления по алгоритмам оптимизации требуют значительного времени, методы оптимального принятия решений ориентированы в основном на их реализацию с помощью компьютерных программ.

Целью коммерческого предприятия является получение прибыли. Любое решение, принятое руководством (будь то решение о количестве купленных товаров, или решение о назначении цены проданного товара, или решение о размещении рекламы в газете и т.д.), повлияет на прибыль в сторону увеличения или уменьшения. Эти решения являются оптимизационными, т.е. всегда есть возможность выбрать лучшее из нескольких возможных решений. Давайте представим, что все управленческие решения принимаются наилучшим образом. То есть все параметры, на которые может влиять фирма, оптимальны. Тогда фирма получает максимальную прибыль (при данных условиях невозможно получить больше). Для определения оптимальности управленческих решений, принимаемых сотрудниками фирмы, можно использовать методы математического программирования.

В экономике проблемы оптимизации возникают из-за многообразия возможных вариантов функционирования конкретного экономического объекта, когда возникает ситуация выбора варианта, лучшего по некоторому правилу, критерия, характеризующегося соответствующей объективной функцией (например, иметь минимум затрат, максимум производства).

Модели оптимизации отражают в математической форме смысл экономической задачи, а характерной особенностью этих моделей является наличие условия для нахождения оптимального решения (критерия оптимальности), которое записывается в виде функционала. Эти модели позволяют, исходя из определенных исходных данных задачи, получить набор решений, удовлетворяющих условиям задачи, и выбрать оптимальное решение, удовлетворяющее критерию оптимальности.

При решении задач оптимизации применяются выводы из теории решений. Существует множество методов определения оптимальных решений вопросов с достаточным количеством ограничений. Некоторые из них: геометрический метод, симплексные методы, динамические методы программирования, методы экспертной оценки и другие.

Самым простым и очевидным методом линейного программирования является графический метод. Используется для решения задач LP с двумя переменными.

Геометрически задача линейного программирования представляет собой поиск такой точки полигона решения, координаты которого обеспечивают максимальное (минимальное) значение линейной объективной функции, а все точки полигона решения являются допустимыми решениями. Решением каждого неравенства системы ограничений FPGA является полуплоскость, содержащая пограничную линию и лежащая на одной стороне пограничной линии. Пересечение полуплоскостей, каждая из которых определяется соответствующим неравенством системы, называется областью допустимых решений или областью детерминации.

Геометрическая интерпретация при решении линейных задач программирования перестает быть пригодной для числа свободных переменных n — m > 3, а для n — m = 3 она уже затруднена. Для решения задачи линейного программирования в общем случае (для любого количества свободных переменных) используются вычислительные, а не геометрические методы. Так называемый симплексный метод является наиболее универсальным среди них.

Метод симплекса является одним из наиболее эффективных методов численного решения задач ЛП. Суть понятия «симплекс» заключается в следующем. Для тела в k-мерном пространстве симплекс — это множество, состоящее из k +1 вершин этого тела. Например, если k = 2, т.е. на плоскости, симплекс — это вершины треугольника; если k = 3, симплекс — это вершины тетраэдра, т.е. тетраэдра и т.п. Метод называется так потому, что он основан на непрерывном перечислении вершин FSTD для определения координат вершины, у которой объективная функция имеет экстремальное значение. Метод был разработан в 1947 году американским математиком Джорджем Данцигом.

Функция, связывающая объективную (оптимизированную переменную) с управляемыми переменными в задаче оптимизации, называется объектной функцией. В самом широком смысле объективная функция — это математическое выражение для критерия качества одного объекта (решения, процесса и т.д.) по сравнению с другим. Примером критерия в теории статистического решения является средний квадратный критерий точности аппроксимации. Цель состоит в том, чтобы найти оценки там, где объективная функция достигает минимума. Важно, чтобы критерий всегда вводился извне, и только тогда будет найдено правило принятия решения, которое минимизирует или максимизирует объективную функцию.

Динамическое программирование

Динамическое программирование — это подполе оптимального программирования, в котором процесс принятия решений и управления можно разбить на отдельные этапы (фазы).

Экономический процесс можно контролировать, если есть возможность влиять на ход его развития. Под управлением понимается ряд решений, принимаемых на каждом этапе для оказания влияния на ход развития процесса. Например, выход компании — это управляемый процесс. Набор решений, принятых в начале года (квартала и т.д.) по обеспечению предприятия сырьем, замене оборудования, финансированию и т.д., является управленческим. Необходимо организовать выпуск продукции таким образом, чтобы решения, принимаемые на каждом этапе, помогали достичь максимально возможного выхода или прибыли.

Динамическое программирование позволяет свести сложную проблему со многими переменными к множеству проблем с небольшим количеством переменных. Это значительно сокращает объем расчетов и ускоряет процесс принятия решений. При решении задачи этим методом процесс решения разбивается на этапы, которые обрабатываются последовательно во времени и в конечном итоге приводят к желаемому решению.

В отличие от линейного программирования, где симплексный метод является универсальным методом решения, в динамическом программировании такого универсального метода нет. Одним из основных методов динамического программирования является метод рекурсивных соотношений, основанный на применении принципа оптимальности, разработанного американским математиком Р. Беллманом. Принцип заключается в том, что независимо от исходного состояния на любом этапе и от выбранного на этом этапе контроля, дальнейший контроль должен быть выбран как оптимальный по отношению к состоянию, которое система будет занимать в конце этого этапа. Применение этого принципа гарантирует, что управление, выбранное на любом этапе, не лучше локально, а лучше по отношению ко всему процессу в целом.

В некоторых задачах, решаемых методом динамического программирования, процесс управления разделен на этапы. При разделении фондов деятельности предприятия на несколько лет полезно рассматривать этот период как этап; при разделении фондов между предприятиями это число следующего предприятия. В других задачах разделение на этапы вводится искусственно. Например, непрерывно управляемый процесс можно считать дискретным, условно разделив его на временные периоды (шаги). Исходя из условий каждой конкретной задачи, длина шага выбирается таким образом, чтобы на каждом шаге получалась простая задача оптимизации и гарантировалась требуемая точность расчетов.

При решении экономических проблем часто анализируются ситуации, в которых сталкиваются интересы двух или более конкурирующих сторон, преследующих разные цели; это особенно характерно для рыночной экономики. Такие ситуации называются конфликтными.

Математическая теория конфликтных ситуаций — это теория игр. В игре могут сталкиваться интересы двух (парная игра) или более (множественная игра) противников; есть игры с бесконечным числом игроков. Во множественном числе, если игроки образуют коалицию, игра называется коалицией; если таких коалиций две, то игра сводится к парной.

На промышленных предприятиях теория игр может быть применена для выбора оптимальных решений, например, при формировании рациональных запасов сырья, полуфабрикатов, когда противопоставляются две тенденции: Увеличение запасов, гарантирующих бесперебойную работу добычи, снижение запасов, минимизирующее затраты на их хранение. В сельском хозяйстве теория игр может быть применена при решении таких экономических задач, как посев одной из возможных культур, урожайность которой зависит от погоды, если известна удельная цена той или иной культуры и средний урожай каждой культуры в зависимости от погоды (например, будет ли лето сухим, нормальным или дождливым); в этом случае ферма, которая хочет получить наибольший доход, действует как одно, так и природа как другая.

Решение таких задач требует полной определенности в формулировке их условий (правил игры); определения количества игроков, идентификации возможных стратегий игроков, возможных прибылей (под убытком понимается отрицательная прибыль). Важным элементом в состоянии игровых заданий является стратегия, т.е. набор правил, которые в зависимости от ситуации в игре определяют уникальный выбор действий данного игрока. Если в ходе игры игрок поочередно использует несколько стратегий, то такая стратегия называется смешанной, а ее элементы — чистыми стратегиями. Количество стратегий каждого игрока может быть конечным и бесконечным, в зависимости от того, какие игры делятся на конечные и бесконечные.

Метод экспертных оценок

В принципе, лицо, принимающее решение, может получить информацию, необходимую для принятия решения, только из трех источников: от личных знаний, собственного опыта и интуиции, от опыта других людей через анализ эмпирических данных и от советов экспертов. Однако при решении действительно сложных, сложных задач, особенно в условиях неопределенности и неполноты информации, зачастую единственным способом как-то определить сложную ситуацию является метод логико-эвристического анализа, основанный на экспертной оценке.

Методы экспертной оценки — это методы организации работы с экспертами и обработки экспертных заключений. Эти мнения обычно выражаются частично в количественной и частично в качественной форме. Экспертные исследования проводятся с целью подготовки информации для принятия решений ЛДП (лицом, принимающим решения). Для проведения работы над методом экспертной оценки от имени ОПП создается рабочая группа (РГ), которая организует деятельность экспертов (формальных или основных), сгруппированных в Экспертной комиссии (ЭК).

Оценки готовятся в форме индивидуальных и коллективных оценок. Индивидуальная оценка — это оценка одного эксперта. Например, преподаватель ставит студенту одну оценку, в то время как врач ставит пациенту диагноз. Но в сложных случаях болезни или когда учащемуся грозит отчисление за плохую успеваемость, запрашивается коллективное мнение — симпозиум врачей или группа преподавателей. В армии ситуация похожа. Обычно командир принимает решение в одностороннем порядке. Но в сложных и критических ситуациях проводится военный совет.

Экспертные оценки часто используются в процессе отбора, например:

Версия технического устройства, которая будет продаваться в серии из нескольких экземпляров;
группа астронавтов из множества претендентов;
Отбор научно-исследовательских проектов для финансирования из массы заявок;
получателей экологических кредитов из числа многих желающих;
в отборе инвестиционных проектов для реализации среди представленных проектов и т.д.

Давайте кратко охарактеризуем ключевые этапы процесса экспертной оценки. В том числе:

Формулировка цели и задач экспертной оценки;
Формирование управленческой команды и формализация решения о проведении экспертизы;
Выбор метода получения экспертной информации и методов ее обработки;
Отбор группы экспертов и, при необходимости, подготовка анкет;
Экспертный опрос (экспертиза);
Обработка и анализ результатов исследований;
Интерпретация полученных результатов;
Написать отчет.

Задача экспертной оценки устанавливается ЛПР (заказчиком). При этом следует учитывать следующие факторы: Достоверность и полнота имеющейся исходной информации, желаемая форма представления результата (качественная или количественная), возможные области использования полученной информации, сроки представления, ресурсы, имеющиеся в распоряжении руководства, возможность привлечения экспертов из других областей знаний и многое другое.

Менеджер по аудиту отвечает за подготовку решения и руководство всей последующей работой. Он определяет состав руководства. Руководящая группа будет предоставлять аудиторам обратную связь. Руководство отвечает не только за всю организационную и плановую работу по созданию благоприятных условий для эффективной творческой деятельности специалистов, но и за аналитическую работу по отбору группы экспертов, определение методов получения и обработки информации, подготовку анкет, содержательную интерпретацию полученных результатов.

Экспертный отбор. Проблема отбора экспертов является одной из самых сложных в теории и практике экспертных исследований. Очевидно, что в качестве экспертов необходимо использовать тех лиц, чье мнение в наибольшей степени способствует принятию соответствующего решения. Необходимо идентифицировать, находить и выбирать таких лиц. Следует четко заявить, что не существует методов отбора экспертов, которые обеспечивали бы успех экспертизы. Необходимо рассмотреть различные другие аспекты процедур отбора экспертов.

Проблему отбора экспертов можно разделить на две части — составление списка возможных экспертов и отбор группы экспертов в соответствии с компетенцией кандидатов.

Составление списка возможных экспертов облегчается при многократном повторении рассматриваемого вида оценки. В таких ситуациях обычно ведется список возможных экспертов, например, в области общественной оценки воздействия на окружающую среду или фигурного катания, из которого можно сделать выбор в соответствии с различными критериями или с помощью псевдослучайного датчика числа (или таблицы).

Метод Снежного кома

Рассмотрим ситуацию, когда экзамен проводится впервые и нет установленных списков экспертов. Но даже в этом случае каждый отдельный эксперт имеет некоторое представление о том, что требуется от эксперта в такой ситуации. Существует полезный «снежный ком» метод составления списка, при котором от каждого специалиста, который может рассматриваться в качестве эксперта по рассматриваемому предмету, получается определенное количество (обычно 5-10) имен людей. Очевидно, что некоторые из этих названий появились раньше в деятельности рабочей группы, другие являются новыми. Каждому новичку задают один и тот же вопрос. Процесс расширения списка останавливается, когда практически не появляется новых имен. В результате получился достаточно обширный список возможных экспертов. Метод «снежного кома» имеет свои недостатки. Количество раундов до остановки процесса расширения снежного кома не может быть предсказано заранее. Более того, понятно, что если на первом этапе все эксперты были из одного «клана», придерживались схожих мнений или занимались подобной деятельностью, то метод «снежного кома», скорее всего, вернет людей из того же «клана». Вы будете скучать по мнениям и аргументам других «кланов». (Под этим подразумевается, что сообщество специалистов фактически разделено на вышеупомянутые «кланы», а общение происходит в основном внутри «кланов». Неформальная структура науки, частью которой являются «кланы», достаточно сложна для изучения. На этом этапе следует отметить, что «кланы» обычно формируются на базе крупных формальных центров (университетов, научно-исследовательских институтов), научных школ).

Не менее сложен вопрос оценки компетентности экспертов. Понятно, что успешность участия в предыдущих экзаменах является хорошим критерием для деятельности снайфера, врача, судьи в спортивных соревнованиях, то есть таких специалистов, которые участвуют в длительной серии подобных экзаменов. Но самое интересное и важное, к сожалению, — это уникальные экспертизы масштабных проектов, не имеющих аналогов. Конечно, использование формальных показателей экспертов (должность, ученая степень и звание, стаж работы, количество публикаций…) может быть инструментарием только в современных быстро меняющихся условиях, хотя такие показатели проще всего применять.

Нередко предлагается использовать методы самооценки и самооценки компетентности экспертов. Обсудим их, начиная с метода самооценки, в котором эксперт сам предоставляет информацию о тех областях, в которых он компетентен, и о тех, в которых он не компетентен. Самооценка компетентности оценивает уровень доверия эксперта, а не его фактическую компетентность. Это тем более верно, что сам термин «компетенция» не имеет строгого определения. Уточнить его можно путем детализации его составляющих, но в этом случае подготовительная часть работы экспертной комиссии усложняется. Нередко эксперт преувеличивает свою фактическую компетентность. Например, большинство людей считают, что они хорошо разбираются в политике, экономике, проблемах образования, семьи и медицины. На самом деле, экспертов (и только знающих людей) в этих областях очень мало. Есть также отклонения в другую сторону, слишком критическое отношение к собственным способностям.

В методе взаимной оценки, помимо возможности личных и групповых симпатий и антипатий, определенную роль играет и низкий уровень осведомленности специалистов о способностях друг друга. В современных условиях только специалисты, работающие вместе в течение многих лет (не менее 3-4), в одной комнате, по одной и той же теме, могут иметь достаточно хорошие знания о работе и навыках друг друга. О таких парах можно сказать, что они «съели много соли вместе». Однако включение таких пар специалистов не очень полезно, поскольку их взгляды слишком схожи из-за сходства их жизни.

Если процедура экспертизы предусматривает прямую связь между экспертами, то необходимо учитывать ряд других обстоятельств. Их личностные (социально-психологические) характеристики имеют большое значение. Например, один «громкоговоритель» может парализовать работу всего комитета на совместном заседании. Срыв может быть также вызван недружественными отношениями между членами комитета и совершенно иным научным и официальным статусом членов комитета. В таких случаях важно следовать правилам процедуры, разработанным рабочей группой.

Необходимо подчеркнуть, что отбор экспертов является одной из основных задач рабочей группы, и никакие методы отбора не освобождают ее от ответственности. Иными словами, в обязанности рабочей группы входит обеспечение компетентности экспертов, их способности принципиально решать поставленные задачи. Важно, чтобы ЛПР утвердила список экспертов. В этом случае ЛДП может как добавить в комитет некоторых экспертов, так и удалить некоторых из них — по своим собственным причинам, которые членам РГ и ИК знать не обязательно.

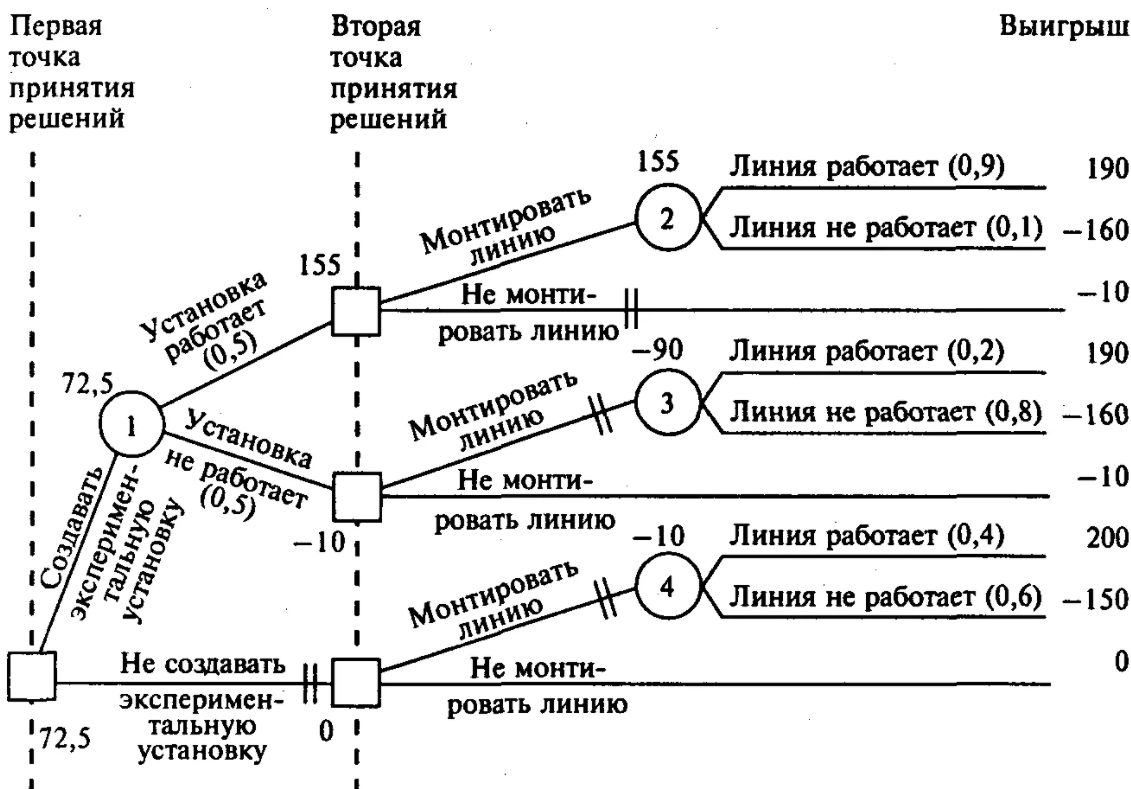
Метод дерева решений

Как выбрать правильное решение из нескольких возможных вариантов? Для определения наиболее подходящего решения специалисты рекомендуют использовать метод дерева решений. Она дает возможность получить подробную модель вероятного развития ситуации или процесса, рассмотреть ее с точки зрения финансовых выгод и рисков, связанных с каждым вариантом действий. С помощью этого прогноза вы можете защитить себя или свою компанию от неэффективных затрат или инвестиций в условиях ограниченных ресурсов. Особенность этого метода принятия решений заключается в том, что мы принимаем решения как на основе вычислений, так и на основе логического рассуждения, когда анализируем факты и приходим к определенному выводу.

Алгоритм применения метода:

Первый пункт решения. Устройство помещается в середине левого края бумаги, представляя собой первую точку принятия решения. Ниже все решения представлены в виде чисел и заключены в квадрат для лучшего зрительного восприятия
возможные действия. Нарисуйте две или более линии от первой точки решения. Количество строк зависит от количества взаимоисключающих вариантов (альтернатив). Сделайте строки как можно шире, чтобы в дальнейшем можно было делать любые необходимые заметки. Над каждой строкой сделать пояснительную записку о возможном направлении действий. Если на этом этапе решение все еще остается неопределенным, т.е. оно еще не может быть принято, то в конце строки ставится круг с буквой. Если эта опция может стать решением, то она помещается в квадрат и получает номер на втором этапе принятия решения.
вероятность событий. В целом, вероятность любого события может быть высокой, средней или низкой. Например, высокий спрос на продаваемую продукцию, средний и низкий спрос. Нарисуйте линии для представления вероятности каждого события. Предположив, что сумма вероятностей равна 100% или единице, найдем ожидаемое соотношение между ними. Например: Высокий — 0,4, средний — 0,3, низкий — 0,3.
ожидаемый результат (прибыль). С правой стороны каждой вероятности записывайте ожидаемые результаты в числовом виде при таком развитии событий.
подсчитать результаты для каждой альтернативы. Для этого необходимо умножить ожидаемый результат (прибыль) на числовую нотацию вероятности, т.е. умножить данные из точек 3 и 4. Таким образом, можно вычислить полученные результаты с разной вероятностью.
сравнение альтернатив. Мы суммируем результаты пункта 5 отдельно по каждому альтернативному варианту. Полученные численные данные для альтернатив сравниваются для выбора наиболее выгодного варианта. Эта наиболее выгодная альтернатива становится второй точкой решения и помещается в квадрат со следующим числом, и так далее в том же порядке.

Таким образом, используя метод «Дерева целей» для принятия решений, можно дополнительно определить пути его развития, сравнивая новые альтернативы с помощью того же метода.

Под названием «транспортная проблема» сгруппированы различные задачи с единой математической моделью. Классической проблемой транспортировки является проблема поиска наиболее экономичного плана транспортировки однородного продукта или взаимозаменяемых изделий из точек производства в точки потребления; чаще всего она встречается в практических приложениях линейного программирования. Линейное программирование — одна из подобластей математического программирования, область математики, развивающая теорию и численные методы решения многомерных экстремальных задач с ограничениями.

Огромное количество возможных вариантов транспортировки затрудняет получение достаточного экономического плана эмпирическим путем или с помощью экспертной оценки. Применение математических и вычислительных методов в транспортном планировании имеет большой экономический эффект. Проблемы транспорта могут быть решены симплексным методом, однако матрица системы ограничений проблемы транспорта настолько своеобразна, что для ее решения были разработаны специальные методы. Эти методы, как и симплексный метод, позволяют найти исходное эталонное решение, а затем, путем усовершенствования, получить оптимальное решение.

В зависимости от того, как представлены ограничения проблемы транспорта, она может быть представлена в виде сети (схема) или матрицы (табличная). Проблема транспортировки также может быть решена с ограничениями и без них.

На странице курсовые работы по менеджменту вы найдете много готовых тем для курсовых по предмету «Менеджмент».

Здесь темы рефератов по менеджменту

Читайте дополнительные лекции: