Оглавление:
Метод Роберваля построения касательных к плоским кривым
Рассмотрим способ построения касательных к плоским кривым второго порядка. Каждую такую кривую можно рассматривать как траекторию материальной точки, находящейся в сложном движении. Абсолютная скорость движения точки по такой кривой будет определять направление касательной к кривой. Для определения направления абсолютной скорости движение материальной точки представляют как сумму двух более простых движений, направления которых могут быть известны.
Пример:
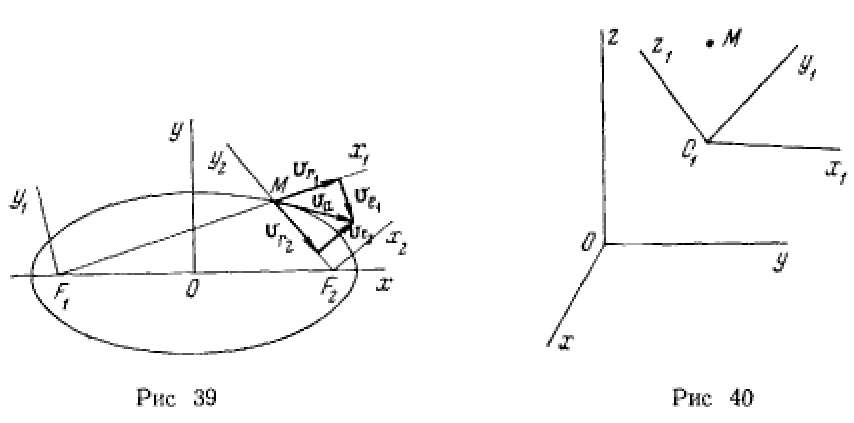
При помощи теоремы о сложении скоростей построить
касательную к эллипсу (рис. 39).
Решение:
Эллипс представляет собой геометрическое место точек, сумма расстояний которых до двух заданных точек (фокусов эллипса) является величиной постоянной
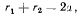
где 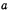 — большая полуось эллипса.
— большая полуось эллипса.
Выберем неподвижную систему осей 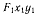 с началом в первом фокусе, направив ось
с началом в первом фокусе, направив ось 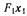 в сторону движущейся по эллипсу точки М. Относительная скорость точки М будет равна скорости изменения расстояния от точки М до фокуса
в сторону движущейся по эллипсу точки М. Относительная скорость точки М будет равна скорости изменения расстояния от точки М до фокуса
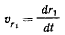
Выбирая вторую подвижную систему координат 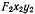 с началом во втором фокусе, направим ось
с началом во втором фокусе, направим ось 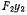 на точку М. Относительная скорость точки М в новой системе координат направлена вдоль оси
на точку М. Относительная скорость точки М в новой системе координат направлена вдоль оси 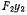 а ее величина равна скорости изменения расстояния от точки М до фокуса
а ее величина равна скорости изменения расстояния от точки М до фокуса 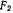
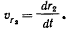
Из уравнения (а) имеем
или

обе системы осей обладают только вращательным движением вокруг
соответствующих фокусов, поэтому переносные скорости будут направлены перпендикулярно к прямым 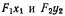 На основании теоремы о сложении скоростей находим положение конца вектора абсолютной скорости, который лежит на пересечении перпендикуляров к прямым
На основании теоремы о сложении скоростей находим положение конца вектора абсолютной скорости, который лежит на пересечении перпендикуляров к прямым 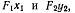 проведенным через концы
проведенным через концы
соответствующих относительных скоростей.
Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:
Предмет теоретическая механика
Эти страницы возможно вам будут полезны:

