


- В этом методе формула (14. 21) получается заранее в следующем формате: Р = Аба \ с ^ с ’^ (14. Пятьдесят одни), где A-константа. Поскольку это уравнение должно быть однородным относительно размеров A, L и T, его можно описать следующим образом: он представляет собой остальные 3 уравнения и 4 индикатора (которые выбираются произвольно, равны единицам индикатора p).Дай (14.52) где(1, f,/ и#могут принимать любые в общем случае, лучше использовать специальную форму(14. 52) нет никаких оснований предполагать, что функция представлена безразмерной переменной. Формула(14. 51), но предположим определить вид 1 члена бесконечного ряда, который может расширить искомую зависимость.
Формула (14. 53) соответствует результатам, полученным для этого вопроса методом Букингема. Фундаментальных инноваций в применении методов размерного анализа к задачам тепломассообмена не существует. Примеры этих дисциплин отложены до той части книги, где конкретно описан теплообмен и массоперенос. Ниже приведен пример, иллюстрирующий весь процесс получения формул с использованием размерного анализа на основе экспериментальных данных. Пример 14.
В связи с детальным изучением теплообмена с кипящей жидкостью, мы измерили скорость и размер образования пузырьков, которые возникают при выходе газа из небольшого отверстия под жидкостью level. To чтобы установить связь между свойствами жидкости и данными о размере пузырьков, необходимо использовать анализ размеров. Предположим, что отношение между размером пузырька и рассматриваемой переменной определяется отношением в виде Г = 6 Ж, А, Р, Е) (1) Где L-диаметр отверстия. Вы можете использовать тесты, чтобы найти 7 из 3 или менее переменных, которые делают невозможным создание безразмерной комбинации. Такими переменными являются d, q.
Эти переменные используются для переменных, которые могут входить в любой из 3 (7-4 = 3) безразмерных комплексов. (Такие переменные всегда содержат произвольные размерные константы. Другие переменные определяются с помощью exception. In в этом случае желательно, чтобы O включал только 1 безразмерный параметр. Хорошо. Термины A, e и e могут быть включены в любой комплекс. Представим в виде а) =(2) =- для N2、 Л2 = / °2b0 в *-(3) При установке размеров Откуда взялась система из 3 уравнений?
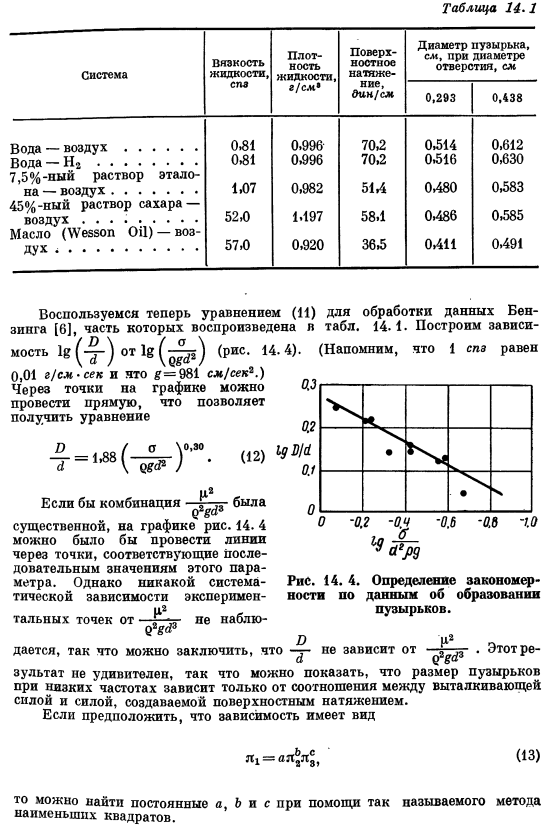
Для b 0 = a-3b + ;; (5) M 0 = 6 + s; (6) Если t0 = — 2s — (7) 1 = −1, находим c = 1, b = −1, a = −2、 (8) Из формулы (9 )) Предположим, вы хотите избежать дробного индикатора, c = 2) (У) Поэтому в результате размерного анализа、 = на_ \ 1 7 \ & P9 /• (11) Таблица 14.1 Система вязкости жидкости, Роспотребнадзор плотность жидкости, г / см * поверхностное натяжение, ПСН / сл » размер пузырька, см, диаметр отверстия, см 0.293 0.438 Вода-воздух 0.81 0.996 70.2 0.514 0.612 Вода-H2 0> 81 0.996 70.2 0.516 0.630 Стандартный 7,5% раствор Воздух-1.07 0.982 514 0480 0.583 45%раствор сахара- Воздух 52.0 1.197 58.1 0486 0.585 Нефть (Uuzz OP) — ВОЗ- Дух 57Y0.
- Теперь мы используем формулу (11) для обработки данных Бензинга [6]. Часть его воспроизведена в таблице. (1 ″» GM 1. 01 г! Cm’SEC и его#= 981 cl / se#.)Вы можете провести прямую линию через точку на графике и получить уравнение. 14.1.Построить его. 18 (-7) из (-55) (14-4). (Помните, что 1 спа равно И » 1 * 88( (12) К2 Сочетание. 14 в таблице. 4 можно провести линию через точку, соответствующую последовательным значениям этого параметра.
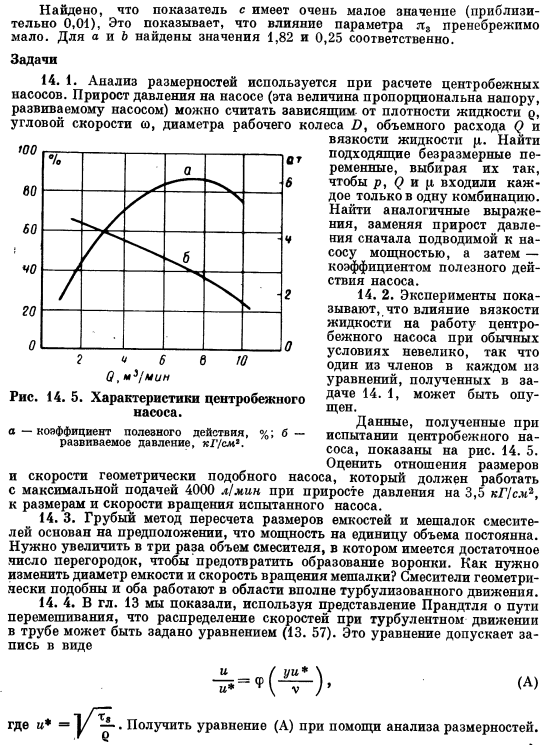
Однако систематической зависимости экспериментальных точек от Ix не наблюдалось Рис.14. 4.Определение рисунка по образованию пены. х Подробнее о R I2 Так что вывод дан-не зависит от Поскольку результаты не удивительны, показано, что размер пузырьков на низких частотах зависит только от соотношения между плавучестью и силой, создаваемой поверхностным натяжением. Предполагая, что зависимость имеет вид (13 )) Затем вы можете найти константы A, B и C, используя так называемый метод наименьших квадратов. Мы видим, что значение показателя c очень мало (около 0,01), и это указывает на то, что влияние параметра незначительно. Значения 1,82 и 0.25 были найдены в A и B, соответственно. Рис.14.
Характеристики центробежных насосов. а-коэффициент полезного действия,%; б-создаваемое давление, кг / см *. Задачи 14. 1.Размерный анализ используется для расчета центробежного насоса. Увеличение давления на насосе (это значение пропорционально давлению, создаваемому на насосе) можно считать зависящим от плотности жидкости p, ec и объемного расхода (>и вязкости жидкости p).p, ( > , p только в 1 комбинации, соответственно. Найдите аналогичную формулу, сначала замените повышение давления на мощность, подаваемую на насос, а затем на эффективность насоса.
Проблема возникает потому, что эксперименты показывают, что влияние вязкости жидкости на работу центробежного насоса в нормальных условиях невелико.14 1 из членов каждого уравнения, полученного в 1, можно опустить. Данные, полученные при испытании центробежного насоса, приведены на рисунке. 14. 5. Увеличение давления на 3,5 КПСМ с максимальным расходом 4000 л / мин для оценки геометрически сходных размеров и скоростных соотношений насоса, проверенных на соответствие размерам насоса и скоростям вращения.
Грубый способ пересчета размеров контейнера и смесителя смесителя основан на предположении, что емкость на единицу объема равна constant. It необходимо увеличить объем миксера на 3 times. In в этом случае имеется достаточное количество перегородок для предотвращения образования воронок. Как изменить диаметр бака и скорость вращения смесителя? Смесители геометрически подобны и оба работают в поле полного турбулентного движения. 14. 4. Ч. 13 используя идею смешивающего тракта Прандтля, распределение скоростей при турбулентном движении в трубе вычисляется по формуле 13.
Смотрите также:
| Пи-теорема Букингема | Баланс механической энергии |
| Модели и подобие | Течение в круглых трубах |
