Оглавление:





Метод релаксации
- Предметом обсуждения является численное решение одного дифференциального уравнения, предложенное Гауссом и позднее воспроизведенное в ряде других работ 2-3 1. Для задачи теплопроводности этот метод был подробно разработан Эммонсом. Об этом говорится в презентации. Рассмотрим первый 2-мерный стационарный случай в декартовых координатах, то есть диапазон дифференциального уравнения. Нарисуйте плоскую деталь на теплопроводе и замените ее. Получившийся в итоге самолет решеткой, состоящей из F и r 63 square.
To метод релаксации: размер ячеек Dx = ^ Dy (рисунок-замещение однородных тел ситом 63).Вместо того, чтобы быть вытащенным из жары Чтобы построить тело как континуум, мы фокусируем процесс тепла Это решетка стержневой влаги. Каждый стержень должен точно передавать количество тепла, которое фактически проходит через поверхностные элементы, по длине、 Ширина соответствует 1 ячейке. В зависимости от этого точка 0 при температуре% получает количество тепла за единицу времени из точки 1(температура bx if-это размер тела в направлении, перпендикулярном плоскости чертежа.
Принято, что газы, которые сначала адсорбировались на поверхности, облегчают образование пузырьков до тех пор, пока они постепенно удаляются с пузырьками. Людмила Фирмаль
Можно написать аналогичную формулу для передачи тепла от узлов решетки 2, 3, 4 к точке 0.Эта сумма Количество тепла определяется мощностью источника (или стока) в точке 0.Источник (или раковина) должен исчезнуть в состоянии равновесия. # Если вы инвестируете концепцию снижения плотности » теплового потока d» =Тогда, очевидно, О Точке 0 Более того, для состояния равновесия d ’= 0 уравнение (536) также может быть интерпретировано как: в равновесии это среднее арифметическое температуры. 4 точки периметра, следовательно Дифференциальные уравнения (53а) могут быть преобразованы в уравнения конечной разности, как уже указано на стр.
Этот случай, оказывается(см. Рисунок 63 для обозначения) Квадратичная производная принимает вид Если вы присвоите эти значения выражению (53a), вы получите: Она прекрасно совпадает с ранее выведенными формулами(536) и(53С).Вот методы смягчения последствий: 1.На основе обсуждения рассматриваемой задачи, включающей в себя весь объем предварительных знаний, в качестве первого приближения выбирается набор значений температуры в узлах. Решетка. Это ^ приближенное решение проверяется от точки к точке в соответствии с требованиями, выраженными в Формуле (53d), то максимальная точка Отклонение.
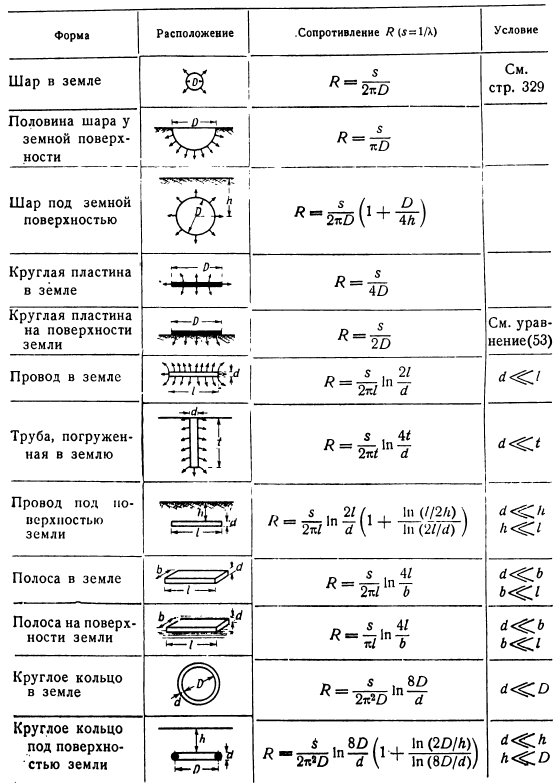
Форма расположение сопротивление=условие Шар Земли 2 1 L » 2 ^ O 329 см. страницу Половину Земли близко к поверхности Земли Шарики под поверхностью Круглая плита на земле Круглая пластина На поверхности Земли Заземляющий провод 777 Гцг Трубы зарыты в землю Провод заземления Полоса на земле Полоса поверхности Круглое кольцо на земле Круговое кольцо под поверхностью Земли, g-4 1P8OA. 1п(2О/Л)\К2к’Р1П(1 \ 1 +1п(8О/ 0 ^»С-Со 3.To в соответствии с формулой (53d), начиная с места максимального отклонения, вводится точечная коррекция. 4.При этих модификациях новые отклонения возникают при соседних points.
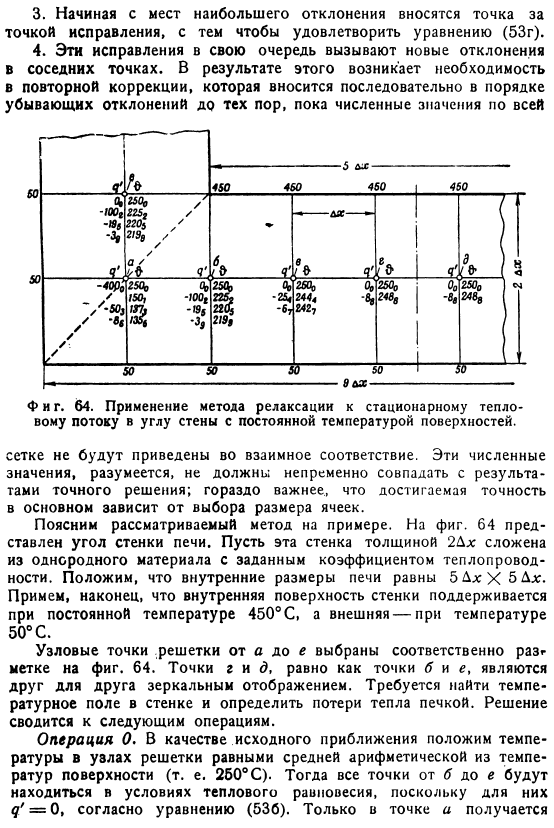
В результате необходимо повторить коррекцию. Порядок, в котором отклонение уменьшается до общего числа Тоже фигура. 64.Применение релаксационного метода к стационарному тепловому потоку в углу стенки, где температура поверхности постоянна. Сетка не совпадает. Конечно, эти цифры не обязательно должны совпадать с точным результатом решения. Гораздо более важно быть достигнутым Точность во многом зависит от выбора размера ячейки. Приведем пример рассматриваемого метода. На рисунке 1 64 показан угол наклона стенки печи. Эта стенка выполнена из однородного материала с заданным коэффициентом толщины 2Dx. Теплопроводность.
- Внутренние размеры печи предполагают 5Dx> 5Dx. Окончательно, внутренняя поверхность стены поддержана на температуре постоянного 450°C, и снаружи- При температуре 50°C узлы решетки от А до Е выбираются в соответствии с метками на рисунке. 64.Точки r и q, а также точки b и e зеркально отражают друг друга. Надо найти Определите температурное поле стен и теплопотери, вызванные печью.
Решение сводится к следующему: Операция 0.As в первом приближении установите температуру точек сетки на среднее арифметическое температуры поверхности (то есть 250°C).Тогда все точки от B до E Согласно формуле (536), они находятся в тепловом равновесии, так как d ’ = 0.Только в точке а?»=-400.Таким образом, принятые на данный момент Температура 250°C, конечно, слишком высока. Операция 1.Согласно формуле (536), температура в точке а уменьшается на^ ’ / 4 = 100°С. Это удовлетворяет условию равновесия. Операция 2.In эта модификация, остаточное значение точки b «=-100 «и сглаживается путем понижения температуры этой точки до D’ / 4 = 25°C.
Рождение новых пузырьков в жидкости является той частью процесса кипения, которая до сих пор не была описана аналитически. Людмила Фирмаль
Все применяется Также для зеркального отражения b, вплоть до точки e. Операция 3.Последняя операция приводит к дисбалансу как a (d ’—25), так и a(d’ =-50).Обратите внимание, что существует двойная ошибка из-за параллелизма Изменяя условия точек b и f, в соответствии с вышеупомянутыми правилами действия, условия точки a корректируются путем понижения температуры на −13°. (Округляется). Дальнейшая работа непосредственно видна из рассмотрения фиг. В 64, номер операции помечается как индекс D ’и числовое значение 0.После 9 операций достигается Равновесное число; это подтверждается окончательной проверкой по формуле (536).
Для определения теплопотерь через углы стенок необходимо учитывать, что площадь Dx / соответствует каждому решетчатому стержню. Поэтому от внутренней поверхности к промежуточной поверхности Стена за единицу времени пропускает тепло 。 Определенное количество тепла перемещается от центральной плоскости к внешней поверхности Истинное значение теплопотерь может быть определено с достаточной точностью как среднее из этих значений. Общее количество тепла, теряемого стеной, очевидно, в 8 раз больше、 Таким образом, он равен 5140) 7. Количество тепла, определяемое при разнице температур 400°с, проходит через прямую стенку площадью, равной внутренней поверхности печи.
Выражение Так, влияние угла на теплопотери характеризуется коэффициентом 5140/4000 = 1,29. Этот результат можно сравнить с выражениями Langmuir, Adams и Makele x>.Таким образом, при определении теплопотерь прямоугольной печи в качестве средней поверхности ПМ、 Ввести значение 。 Где Р-внутренняя поверхность печи, 5-толщина стенок, е / — сумма длин всех поверхностей (внутри).Уравнение справедливо только для / > 0.25.In этот пример, P ^ −20 ^ x1,$ = 2Dx и E / = 4 /. Итак, если мы проигнорируем пункт 3, то получим значение Pm / P { = \ , 22 для искомого коэффициента.
Учитывая большой размер ячейки, используемой в Чтобы решить задачу методом релаксации, мы должны воспринимать это соответствие как удовлетворительное. 2> Решение методом релаксации также может быть выполнено при безразмерной температуре 4). Таким образом, вы получите более общий результат. Как расслабиться Это также относится к проблеме нестационарной теплопроводности. При этих условиях, как указывал Эммонс, для 1-мерного он будет таким же, как и графический метод Биндера-Шмидта. Описание того, как расслабиться, должно быть дополнено многими методами.
Смотрите также:

