Оглавление:
Разложение на множители
Это общий метод, который может быть использован при решении любых, не обязательно алгебраических, уравнений и неравенств. Под разложением на множители некоторого многочлена, вообще говоря, произвольного вида (алгебраического, тригонометрического и т.д.) понимают его представление в виде произведения нескольких сомножителей. В результате разложения на множители решаемое уравнение оказывается сведено к решению на ОДЗ совокупности нескольких, как правило, более простых уравнений. Для разложения на множители существуют различные приёмы, включая группировку и вынесение общего множителя за скобку, одновременное прибавление и вычитание некоторого одночлена или же, наоборот, разбиение одночлена на сумму (разность) нескольких, и другие.
При решении неравенств разложение на множители часто используют для приведения неравенства к виду, удобному для последующего применения метода интервалов.
Пример №348.
Решить неравенство
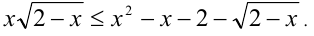
Решение:
Преобразуем неравенство к виду
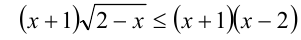
откуда получаем следующее разложение на множители
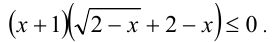
Так как на ОДЗ 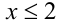 , то рассмотрим два случая. Если
, то рассмотрим два случая. Если 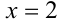 , то неравенство, очевидно, выполняется. Если
, то неравенство, очевидно, выполняется. Если 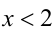 , то сократим на
, то сократим на 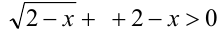 , получив равносильное неравенство
, получив равносильное неравенство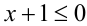 , т.е.
, т.е.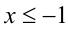 . Объединяя, получаем ответ:
. Объединяя, получаем ответ: 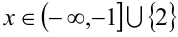 .
.
Пример №349.
Решить уравнение
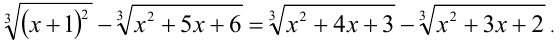
Решение:
Найдя корни, разложим квадратные трёхчлены под радикалами на линейные множители:
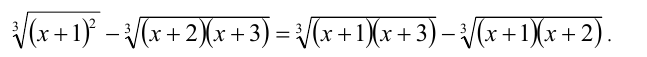
Далее, группируя и вынося общие множители за скобки, получим
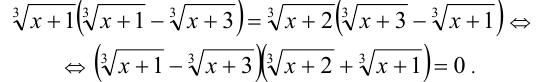
Заметим, что выражение в первых скобках в нуль не обращается. Таким образом, исходное уравнение равносильно уравнению
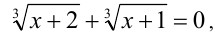
решая которое находим единственный корень 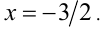
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

