Метод проекций. Образование чертежа по Монжу. Проекции точки
Метод проекций. Проекции центральные и параллельные. Параллельное прямоугольное (ортогональное) проецирование. Свойства параллельного проецирования. Метод Г. Монжа.
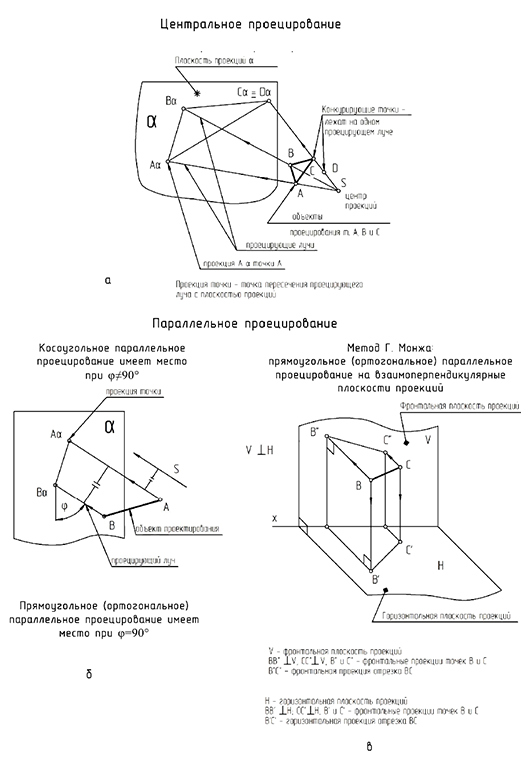
Метод проекций предполагает наличие плоскости проекций, объекта проецирования и проецирующих лучей. Проекции могут быть центральными и параллельными. Если все проецирующие лучи проходят через одну точку, называемую центром проекций 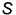 , то проекции называются центральными. Если проецирующие лучи параллельны между собой, то проекции называются параллельными.
, то проекции называются центральными. Если проецирующие лучи параллельны между собой, то проекции называются параллельными.
На рис. 1.1, а показано построение центральных проекций точек 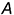 и
и 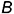 (объекты проецирования) на некоторую плоскость проекций
(объекты проецирования) на некоторую плоскость проекций 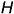 . Проецирующие лучи, проведенные через центр проекций точку
. Проецирующие лучи, проведенные через центр проекций точку 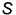 и заданные точки
и заданные точки 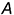 и
и 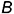 , пересекаются с плоскостью проекций
, пересекаются с плоскостью проекций 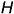 и определяют центральные проекции
и определяют центральные проекции 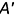 и
и 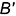 точек
точек 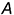 и
и 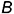 .
.
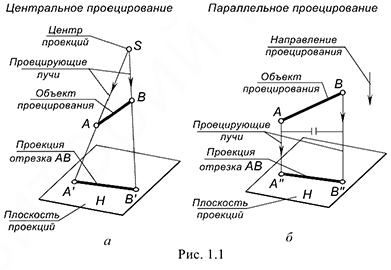
На рис. 1.1,6 показано построение параллельных проекций точек 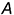 и
и 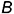 (объекты проецирования) по заданному направлению проецирующих лучей
(объекты проецирования) по заданному направлению проецирующих лучей 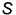 на некоторую плоскость проекций
на некоторую плоскость проекций 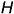 . В результате проецирования на плоскости проекций
. В результате проецирования на плоскости проекций 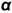 построены параллельные проекции
построены параллельные проекции 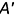 и
и 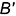 взятых в пространстве точек
взятых в пространстве точек 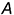 и
и 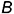 .
.
Запомните! Проекцией точки называется точка пересечения проецирующего луча с плоскостью проекций.
Соединив прямой линией взятые точки 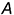 и
и 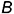 мы получим отрезок
мы получим отрезок 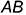 , а соединив прямой линией построенные проекции точек мы получим центральную (рис. 1.1, а) и параллельную (рис. 1.1,6) проекции отрезка
, а соединив прямой линией построенные проекции точек мы получим центральную (рис. 1.1, а) и параллельную (рис. 1.1,6) проекции отрезка 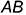 на плоскости проекций
на плоскости проекций 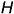 .
.
Параллельные проекции могут быть прямоугольными (ортогональными) или косоугольными:
- если проецирующие лучи перпендикулярны плоскости проекций, то проекции (или проецирование) называются прямоугольными (ортогональными);
- если проецирующие лучи не перпендикулярны плоскости проекций (угол проецирования не равен 90°), то проекции называются косоугольными.
Отметим некоторые свойства параллельного проецирования:
- проекцией точки является точка;
- проекцией прямой линии в общем случае является прямая;
- если отрезок прямой делится точкой в определенном отношении, то проекции прямой делятся проекцией точки в том же отношении;
- если прямые в пространстве параллельны, то их одноименные проекции на чертеже также параллельны.
Точка в системе плоскостей проекций 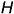 ,
, 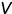 и
и 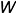 . Проекции точки в системе прямоугольных координат
. Проекции точки в системе прямоугольных координат 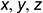 .
.
Для получения изображений предметов на чертежах французский геометр Гаспар Монж предложил следующий метод — метод параллельного прямоугольного проецирования на взаимно перпендикулярные плоскости проекций.
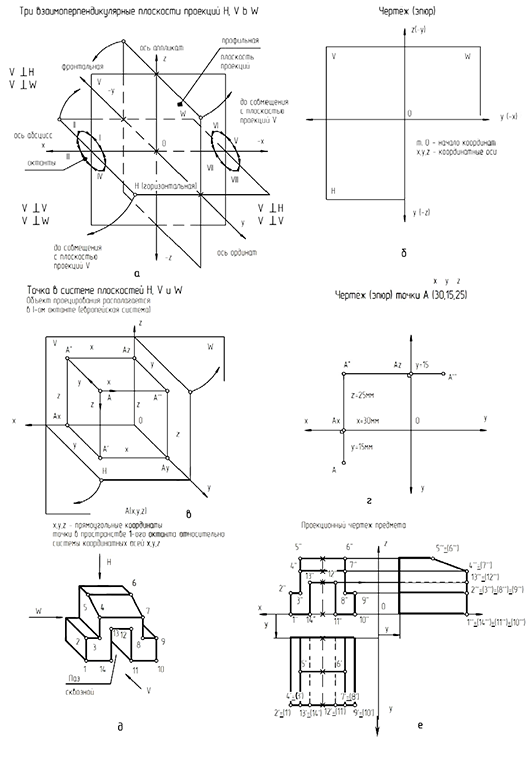
На рис. 1.2, а показано наглядное изображение трех взаимно перпендикулярных плоскостей проекций:
- фронтальная плоскость проекций
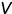 ;
; - горизонтальная плоскость проекций
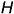 ;
; - профильная плоскость проекций
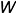 .
.
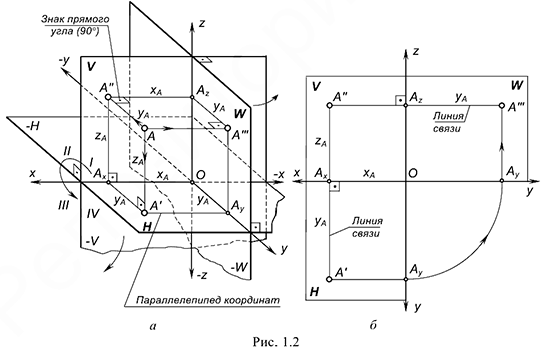
Плоскости проекций, пересекаясь в пространстве, делят пространство на восемь частей, которые называют октантами. Слева от плоскости проекций 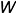 располагаются 1, 2, 3 и 4 октанты, пронумерованные против часовой стрелки. Для получения изображений предмет располагают в 1-м октанте (европейская система) между наблюдателем и плоскостью проекций и проецируют его на каждую из взаимно перпендикулярных плоскостей проекций
располагаются 1, 2, 3 и 4 октанты, пронумерованные против часовой стрелки. Для получения изображений предмет располагают в 1-м октанте (европейская система) между наблюдателем и плоскостью проекций и проецируют его на каждую из взаимно перпендикулярных плоскостей проекций 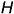 ,
, 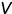 и
и 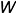 , построив соответственно горизонтальную, фронтальную и профильную проекции предмета.
, построив соответственно горизонтальную, фронтальную и профильную проекции предмета.
В качестве объекта проецирования на рис. 1.2, а взята точка 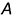 и построены ее прямоугольные проекции на каждую плоскость проекций:
и построены ее прямоугольные проекции на каждую плоскость проекций:
- —
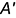 — горизонтальная проекция точки;
— горизонтальная проекция точки; 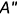 — фронтальная проекция точки;
— фронтальная проекция точки;- —
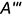 — профильная проекция точки.
— профильная проекция точки.
Плоскости проекций пересекаются между собой по линиям, которые называют осями проекций: ось 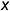 , ось
, ось 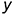 и ось
и ось 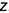 .
.
Оси проекций принимают за оси координат, определяющих положение точки в пространстве, и называют системой прямоугольных координат 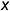 ,
, 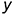 и
и 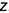 . Оси проекций пересекаются в точке
. Оси проекций пересекаются в точке 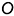 — это точка начала координат.
— это точка начала координат.
Расстояния точки 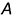 от каждой плоскости проекций определяют ее положение в пространстве и называются ее прямоугольными координатами:
от каждой плоскости проекций определяют ее положение в пространстве и называются ее прямоугольными координатами:
- координата
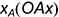 — расстояние от плоскости проекций
— расстояние от плоскости проекций 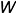 (абсцисса);
(абсцисса); - координата
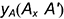 — расстояние от плоскости проекций
— расстояние от плоскости проекций 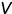 (ордината);
(ордината); - координата
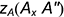 — расстояние от плоскости проекций
— расстояние от плоскости проекций 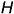 (аппликата).
(аппликата).
Чтобы перейти от наглядного изображения системы трех плоскостей проекций 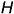 ,
, 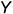 и
и 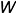 и получить чертеж (эпюр), плоскости проекций первого октанта повертывают относительно координатных осей и совмещают с фронтальной плоскостью проекций
и получить чертеж (эпюр), плоскости проекций первого октанта повертывают относительно координатных осей и совмещают с фронтальной плоскостью проекций 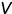 следующим образом:
следующим образом:
- фронтальная плоскость проекций
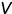 сохраняет свое положение;
сохраняет свое положение; - горизонтальную плоскость проекций
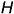 поворачивают относительно оси проекций
поворачивают относительно оси проекций 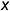 вниз;
вниз; - профильную плоскость проекций
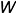 поворачивают относительно оси проекций
поворачивают относительно оси проекций 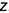 вправо.
вправо.
На чертеже (см. рис. 1.2, б) координатные оси проекций располагают следующим образом:
- ось
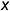 — горизонтально;
— горизонтально; - ось
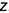 — вертикально;
— вертикально; - ось
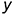 — раздваивается и проводится как продолжение осей
— раздваивается и проводится как продолжение осей 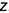 и
и 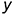 от точки
от точки 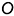 — начала координат.
— начала координат.
Чертеж предмета содержит изображения проекций этого предмета.
Проекции предмета строятся как проекции совокупного множества точек, определяющих и задающих поверхность этого предмета. Точки объединяются в более общие известные из геометрии элементы: прямые, плоскости и различные поверхности (гранные, цилиндрические, конические и т. д.).
Чертеж точки содержит ее проекции, которые строятся по координатам этой точки.
На рис. 1.2, б показано построение чертежа произвольной точки 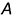 , заданной на рис. 1.2, а, положение которой в пространстве определяют координаты
, заданной на рис. 1.2, а, положение которой в пространстве определяют координаты 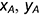 и
и 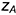 . Для построения чертежа этой точки выполнены следующие графические действия:
. Для построения чертежа этой точки выполнены следующие графические действия:
- влево от точки
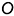 по оси
по оси 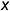 отложен отрезок
отложен отрезок  — координата
— координата 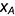 ;
; - вниз от точки
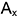 отложен отрезок
отложен отрезок 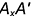 — координата
— координата 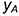 (отрезок
(отрезок 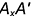 на чертеже в 2 раза больше, чем на наглядной картине) и построена горизонтальная проекция
на чертеже в 2 раза больше, чем на наглядной картине) и построена горизонтальная проекция 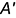 точки
точки 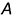 .
. - вверх от точки
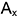 отложен отрезок
отложен отрезок 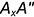 — координата
— координата 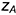 и построена фронтальная проекция
и построена фронтальная проекция 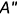 точки
точки 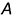 .
.
!!! Запомните! Горизонтальная 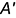 и фронтальная
и фронтальная 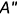 проекции точки лежат на одной вертикальной линии, перпендикулярной оси
проекции точки лежат на одной вертикальной линии, перпендикулярной оси 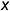 , которая называется линией связи.
, которая называется линией связи.
Чтобы построить профильную 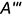 проекцию точки, следует провести горизонтальную линию связи, перпендикулярную оси проекций
проекцию точки, следует провести горизонтальную линию связи, перпендикулярную оси проекций 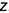 , и отложить от полученной точки
, и отложить от полученной точки 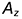 отрезок
отрезок 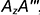 равный координате
равный координате 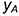 (или отложить от точки
(или отложить от точки 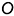 вправо по оси
вправо по оси 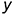 отрезок
отрезок 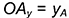 и провести вертикальную линию до пересечения с линией связи от фронтальной проекции точки
и провести вертикальную линию до пересечения с линией связи от фронтальной проекции точки 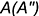 .
.
!!! Запомните! Фронтальная 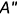 и профильная
и профильная 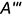 проекции точки лежат на одной горизонтальной линии связи, перпендикулярной оси проекций
проекции точки лежат на одной горизонтальной линии связи, перпендикулярной оси проекций 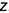 .
.
На рис. 1.3 показано построение чертежа точки 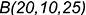 по заданным (в скобках) координатам
по заданным (в скобках) координатам 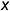 ,
, 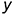 и
и 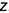 в миллиметрах. Выполнены следующие графические построения:
в миллиметрах. Выполнены следующие графические построения:
- проведены оси координат
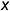 ,
, 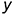 и
и 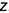 на поле чертежа;
на поле чертежа; - от точки
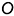 влево отложен отрезок
влево отложен отрезок 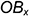 -координата
-координата 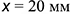 и через точку
и через точку 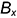 проведена вертикальная линия связи;
проведена вертикальная линия связи; - вниз от точки
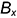 по линии связи отложен отрезок
по линии связи отложен отрезок 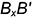 — координата
— координата 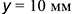 и построена горизонтальная проекция
и построена горизонтальная проекция 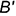 точки
точки 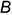 ;
;
- вверх от точки
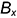 по линии связи отложен отрезок
по линии связи отложен отрезок 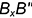 — координата
— координата 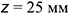 и построена фронтальная проекция
и построена фронтальная проекция 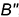 точки
точки 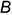 ;
; - проведена горизонтальная линия связи от фронтальной проекции
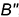 ;
; - от точки
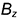 отложен вправо отрезок
отложен вправо отрезок 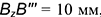 , равный координате
, равный координате 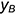 , и построена профильная проекция
, и построена профильная проекция 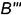 точки
точки 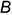 .
.
Структуризация материала первой лекции в рассмотренном объеме схематически представлена на рис. 1.4 (лист 1). На последующих листах 2 и 3 повторно приведены иллюстрации к этой схеме, способствующие закреплению изученного материала и его быстрому визуальному повторению (рис. 1.5 и 1.6).
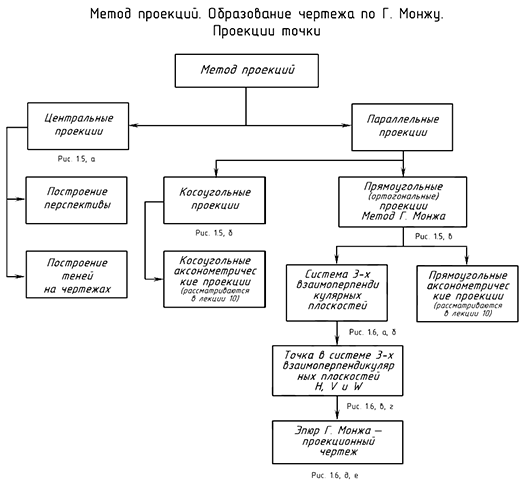
Аппарат проецирования объект проецирования; плоскость проекций; направление проецирующих лучей.
Проекции называют центральными, если проецирующие лучи исходят из одной точки, называемой центром проекций 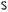
Проекции называют параллельными, если проецирующие лучи параллельны (центр проекций удален в бесконечность).
Параллельные проекции могут быть
• Косоугольными, если проецирующие лучи не перпендикулярны плоскости проекций
• Прямоугольными, если проецирующие лучи перпендикулярны плоскости проекций
На чертеже
Точки обозначаются прописными буквами латинского алфавита 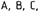 … и т.д, или арабскими цифрами 1, 2, 3, и т.д. Проекции точек обозначаются теме же буквами, или цифрами, но со штрихами
… и т.д, или арабскими цифрами 1, 2, 3, и т.д. Проекции точек обозначаются теме же буквами, или цифрами, но со штрихами 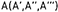 и т.д.;
и т.д.; 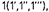 ,
, 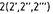 и т.д
и т.д
Линии обозначаются строчными латинскими буквами 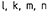 и т.д. Их проекции обозначаются теме же буквами, но со штрихами
и т.д. Их проекции обозначаются теме же буквами, но со штрихами 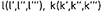 и т.д
и т.д
Плоскости обозначаются греческими буквами 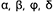 и т.д. Их проекции обозначаются теме же буквами, но со штрихами
и т.д. Их проекции обозначаются теме же буквами, но со штрихами 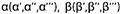 и т. д.
и т. д.
Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:
Начертательная геометрия для 1 курса
Возможно эти страницы вам будут полезны:

