Оглавление:
Метод проекции градиента
Естественны и другие попытки применить методы безусловной оптимизации для решения задач математического программирования. Одним-из них является метод проекции градиента (МПГ), базирующийся на биоритме градиентного спуска безусловной оптимизации. Другими словами, МПГ — численный метод условной оптимизации для нелинейных задач. Рассмотрим задачу:
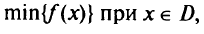
где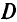 
— замкнутое выпуклое множество в 
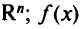— дифференцируемая функция на множестве .
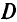Проекцией точки а на множество 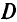называется точка 
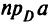, ближайшая к а среди всех точек 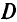, т.е. 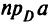является решением задачи проектирования:
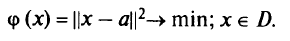
Свойства проекции точки на множество определяются следующими леммами и теоремой.
Лемма 1. Пусть 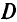— замкнутое выпуклое множество в 
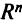. Тогда:
1) проекция 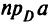а любой точки 
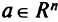существует и единственна;
2) точка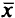 
является проекцией точки а на множество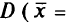 
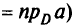в том и только в том случае, если
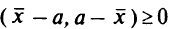
при всех
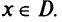
3) для любых точек
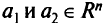
справедливо неравенство
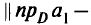
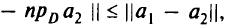
оператор проектирования обладает свойством нерастяжения.
Доказательство. 1. Функция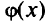 
есть строго выпуклая функция, поэтому решение задачи (5.30) существует и единственно.
На выпуклом множестве и при выпуклой функции 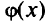, если 
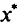есть локальное решение задачи (5.29), должно выполняться условие
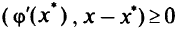
при всех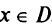 
.
Производная
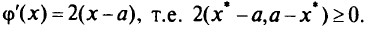
В силу утверждения 2 имеем
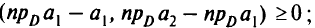
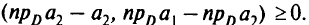
Сложив эти неравенства, получим
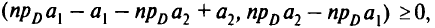
что в силу неравенства Коши-Буняковского дает
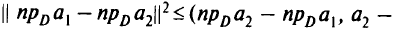
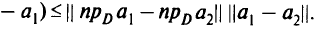
Необходимые и достаточные условия оптимальности в выпуклой задаче на языке проекций формулируются следующим образом.
Лемма 2. Пусть множество 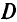выпукло и замкнуто, функция 
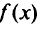выпукла на 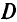и дифференцируема в точке 
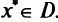. Тогда 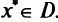является решением задачи (5.29) в том и только в том случае, если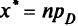 
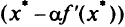при произвольном 
.
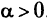Доказательство. Согласно п. 2 леммы 1 приведенное равенство эквивалентно условию
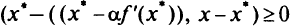
при всех 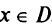. Поэтому
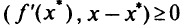
при всех 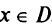. А это и есть условие решения задачи (5.29).
В методе градиентного спуска определяется последовательность точек
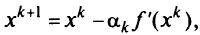
в методе проекции градиента на каждой k-й итерации требуется производить операцию проектирования точки на множество 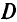т.е. решать задачу (5.30) при
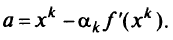
В качестве очередной точки приближения к решению задачи (5.29) выбирается точка
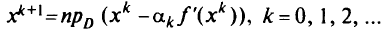
Сходимость последовательности (5.31) к решению задачи (5.29) гарантируется следующей теоремой.
Теорема. Пусть множество 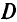выпукло и замкнуто, функция 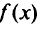строго выпукла на 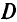c константой 
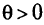и дифференцируема на 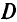, причем ее градиент удовлетворяет условию Липшица
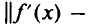
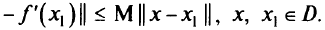
Тогда последовательность, генерируемая по правилу (5.31), где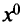 
— произвольная точка из множеств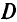а , а
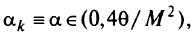
сходится к решению 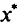задачи (5.29) со скоростью геометрической прогрессии:
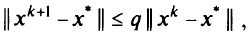
где
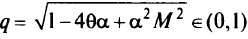
(без доказательства).
Конкретных рекомендаций для выбора значений 8 нет, поэтому значения а выбирают из опыта. В общем случае на каждой итерации надо решать задачу (5.30). Но для некоторых множеств 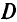удается получить явный вид проекций:
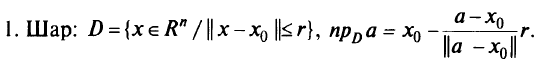
А линейно независимы,
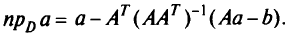
Если множество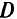 
задается с помощью более или менее сложной системы равенств и неравенств, то метод проекции градиента практически не применим — задача (5.30) не проще исходной задачи.
Пример:
Найти
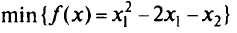
при ограничениях
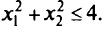
Здесь множество 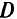— круг радиуса 
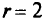с центром в начале координат 
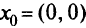, т.е. это шар. Последовательность точек в методе проекции градиента задается формулой
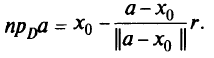
Пусть нулевое приближение
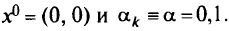
Производные
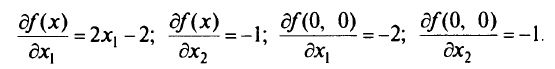
Тогда, согласно (5.31),точка
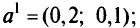
длина вектора
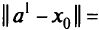
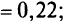
согласно (5.32) проекция
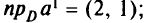
значение целевой функции
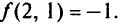
На следующем шаге имеем
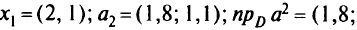
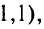
значение целевой функции
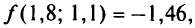
т.е. движение идет в правильном направлении: оптимальное решение имеет координаты (0,75; 1,85) и значение целевой функции равно (—2,8).
Эта теория взята со страницы лекций по предмету «математическое программирование»:
Предмет математическое программирование
Возможно эти страницы вам будут полезны:
