Оглавление:
Метод полного исключения Жордана для решения систем линейных алгебраических уравнений
На каждом шаге симплекс-метода требуется определять новые «наборы» базисных и свободных переменных, т.е. решать системы линейных алгебраических уравнений. Задачи линейного программирования решают с помощью стандартных симплекс-таблиц, формализующих алгоритм перевода базисных переменных в свободные. Этот алгоритм и определяет конкретный вид симплекс-таблиц. Рассмотрим симплекс-таблицы, преобразуемые с помощью метода полного исключения Жордана, получившего наибольшее распространение в линейном программировании.
Рассмотрим систему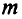 
линейных алгебраических уравнений с 
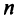неизвестными:
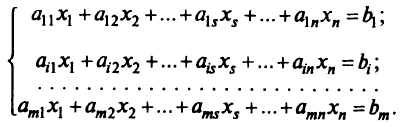
В методе ‘полного’ исключений Жордана делают такие преобразования, в результате которых в каждой строке и в каждом столбце матрицы системы линейных алгебраических уравнений остаются по одному неизвестному с коэффициентами, равными единице. Например, мы хотим исключить переменную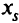 
из всех строк за исключением 
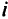-й строки. Элемент 
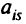— коэффициент, стоящий перед переменной 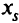, называют генеральным элементом, 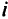-ю строку и 
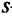-й столбец — разрешающими. Прежде всего разрешающую строку делят на 
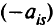, и она остается неизменной. Чтобы исключить 
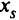из первого уравнения, умножим разрешающую строку на 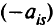и сложим с первой строкой. В результате получим первую строку с нулевым элементом на месте Аналогично исключаем 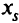в остальных строках. Получим новую эквивалентную запись системы алгебраических уравнений. В ней 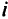-я строка имеет прежний вид, но все коэффициенты у нее поделены на 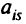;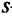-й столбец состоит из нулевых элементов (кроме единицы, стоящей в 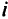-й строке). Остальные элементы матрицы системы и столбец свободных членов пересчитываются по правилу прямоугольника. Например, новое значение элемента 
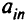будет равна
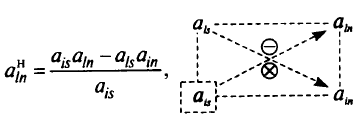
а новое значение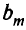 
столбца свободных членов —
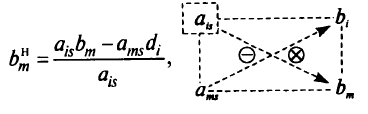
Из правила прямоугольника следует, что когда в разрешающей строке (столбце) есть нулевые элементы, то элементы столбцов (строк), пересекающих эти нулевые элементы, остаются без изменения.
В процессе решения задачи линейного программирования симплекс-методом возможно «зацикливание». Поясним его суть. Пусть в процессе решения задачи линейного программирования на некотором шаге симплекс-метода наименьших положительных отношений свободных членов к элементам разрешающего столбца оказалось больше одного, т.е. выбор разрешающего элемента неоднозначен. После этого шага все упомянутые свободные члены, за исключением свободного члена разрешающей строки, обратятся в нуль. Этот случай называют вырождением: сливаются две или большее число вершин выпуклого многогранника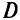 
, когда ребро (или ребра), соединяющие эти вершины, стягиваются в точку.
В алгоритме симплекс-метода каждый шаг означает переход по ребру от данной вершины многогранника 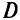к соседней (расположенной на том же ребре), а при вырождении — совпадение двух соседних вершин — алгоритм может потерять монотонность, т.е. может случиться, что после указанного шага мы остались в той же вершине, только выраженной с помощью другого набора из 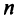уравнений, относящихся к этой вершине. Если продолжать решение симплекс-методом, то не исключено, что после некоторого числа шагов мы вернемся к уже взятой ранее вершине и процесс начнет повторяться. Произойдет зацикливание. Если в процессе решения проводилось запоминание уже испытанных ребер, то для прерывания зацикливания достаточно сменить генеральный элемент.
Существуют алгоритмы, где автоматически предусмотрены меры против зацикливания — «расклеивание» слипшихся вершин.
Как спланировать выпуск продукции пошивочному предприятию
Выпуск продукции пошивочного предприятия может быть определен из решения задачи линейного программирования. Решать ее будем симплекс-методом. Формулировку задачи и процедуру применения симплекс-метода рассмотрим на конкретном примере.
Задача:
Намечается выпуск двух видов костюмов — мужских и женских. На женский костюм требуется 1 м шерсти, 2 м лавсана и 1 чел.-день трудозатрат; для мужского костюма — 3,5 м шерсти, 0,5 м лавсана и тоже I чел.-день трудозатрат. На пошив этих костюмов имеется 350 м шерсти, 240 м лавсана и 150 чел.-дней трудозатрат. По плану костюмов не должно быть менее 110 штук и необходимо обеспечить прибыль не менее 1400 руб. Требуется определить оптимальное число костюмов каждого вида, обеспечивающее максимальную прибыль, если прибыль от реализации женского костюма составляет 10 руб., а от мужского — 20 руб.
Решение. Пусть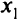 
— число женских костюмов, а 
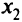— мужских. Прибыль от женских костюмов составляет 10 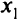руб., а от мужских 20 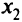руб., т.е. необходимо максимизировать целевую функцию
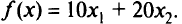
Расход шерсти составляет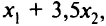 
лавсана 
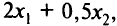трудовых ресурсов 
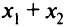. Поэтому ограничения задачи имеют вид:
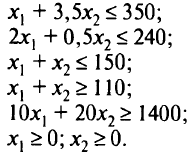
Первые три неравенства описывают ограничения по ресурсам, четвертое и пятое — соответственно плановое задание по общему числу костюмов и ограничение по прибыли.
Для решения задачи симплекс-методом сведем систему ограничений к равенствам путем введения неотрицательных слабых переменных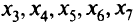 
(в первом и втором ограничениях проведем умножение на 2, а в пятом сократим обе части неравенства на 10):
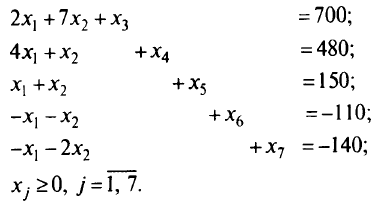
Первым этапом в симплекс-методе является отыскание опорного решения — допустимого базисного решения, с которого начинается поиск оптимального решения. Чтобы решение было опорным, базисные переменные должны быть неотрицательны, т.е. элементы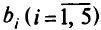 
столбца свободных членов должны быть неотрицательны. В задачах небольшой размерности опорное решение легко увидеть. В нашем случае самое простое — это в качестве базисных переменных взять 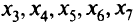, но такое базисное решение не является допустимым (опорным), так как 
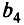и 
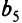отрицательны. Для поиска опорного решения надо сформулировать дополнительную фиктивную целевую функцию 
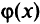, элементы которой равны сумме элементов строк, отражающих те ограничения, где 
.
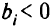В симплекс-таблице для 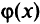отводится своя строка, получаемая суммированием соответствующих элементов строк с отрицательными значениями 
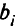(в нашем случае 4-я и 5-я строки). С помощью симплекс-метода фиктивная целевая функция максимизируется. Если 
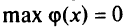и при этом все коэффициенты в строке для 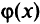нулевые, то базисное решение, соответствующее этой таблице, будет опорным. Тогда, исключая строку для 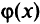, переходим к отысканию оптимального решения исходной задачи. Если 
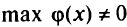, то система ограничений задачи противоречива. Может иметь место случай, когда 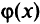достигла своего максимума, равного нулю, а среди элементов строки 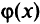есть ненулевые элементы. Это означает, что соответствующие переменные, в столбцах для которых есть ненулевые элементы, тождественно равны нулю и могут быть исключены из рассмотрения. Исходная таблица симплекс-метода для нашей задачи имеет вид табл. 2.1.
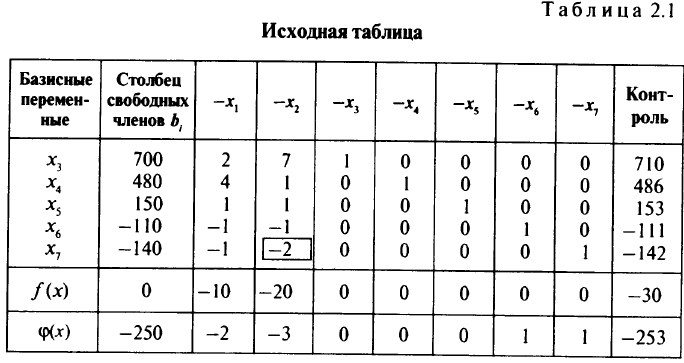
Данные табл. 2.1 соответствуют системе ограничений-равенств (2.2). Так, согласно этой таблице
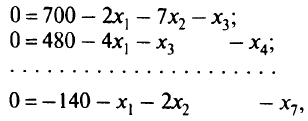
что соотносится с системой уравнений (2.2). Согласно табл. 2.1
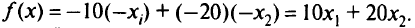
Последний контрольный столбец содержит сумму всех чисел в строке, в процессе пересчетов сумма всех чисел в строках должна быть равной числу в контрольном столбце.
Проведем максимизацию функции 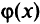. Среди элементов строки 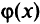есть отрицательные. Берем меньший отрицательный коэффициент, равный -3; он указывает, что переменную 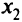надо перевести в базисные. Чтобы определить, какую переменную следует из базисных перевести в свободные, рассмотрим положительные отношения 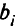к соответствующим элементам столбца 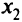: 700/7= 100; 480/1=480; 150/1 = 150;-110/(-1) = 110;-140/(-2)= 70. Минимальное значение, равное 70, указывает, что 
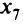надо перевести в свободные, а генеральным {разрешающим) элементом является (-2) (обведен). Для получения следующей симплекс-таблицы применим метод полного исключения Жордана (табл. 2.2).
Разрешающую строку (для 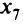) делим на (-2) и заносим в табл. 2.2; столбец 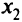заполняем нулями. Столбцы для 
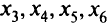переносим без изменения, так как они пересекают нулевые элементы раз-
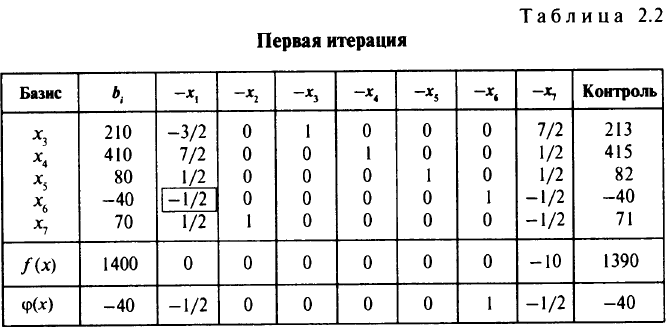
решающей строки. Остальные элементы таблицы пересчитываем по правилу прямоугольника. Проверяем, совпадает ли сумма чисел в строке с числом в контрольном (последнем) столбце. Если совпадения нет, произошла ошибка в расчете. Вместе с функцией 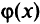пересчитывают и целевую функцию 
.
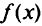Продолжаем максимизировать 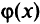. В базисные переменные можно перевест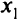и и 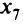, так как для них есть отрицательные коэффициенты в строке 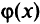. Переводим 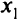в базисные переменные. По минимуму положительных отношений 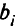к элементам столбца (—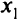) выбираем элемент 
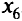, который надо перевести в свободные, генеральный элемент — (-1/2), разрешающую строку для 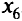и разрешающий столбец для 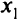. Получим табл. 2.3.
Из табл. 2.3 видно, что достигнут максимум фиктивной целевой функции (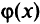 = 0), и все коэффициенты в строке 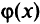равны
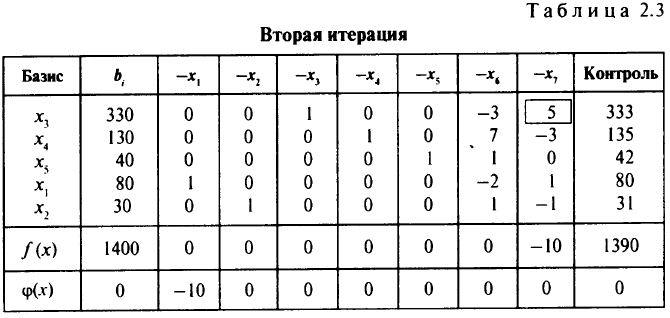
нулю, т.е. получено опорное решение
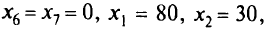
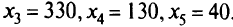
Это решение не является оптимальным, так как в строке 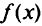имеется отрицательный коэффициент.
Продолжаем улучшать решение симплекс-методом. Строку 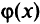исключаем. Генеральным будет элемент (1, 7), равный 5; 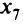переводим в базис (вместо 
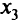). Получим табл. 2.4, затем табл. 2.5. В табл. 2.4 отмечен генеральный элемент.
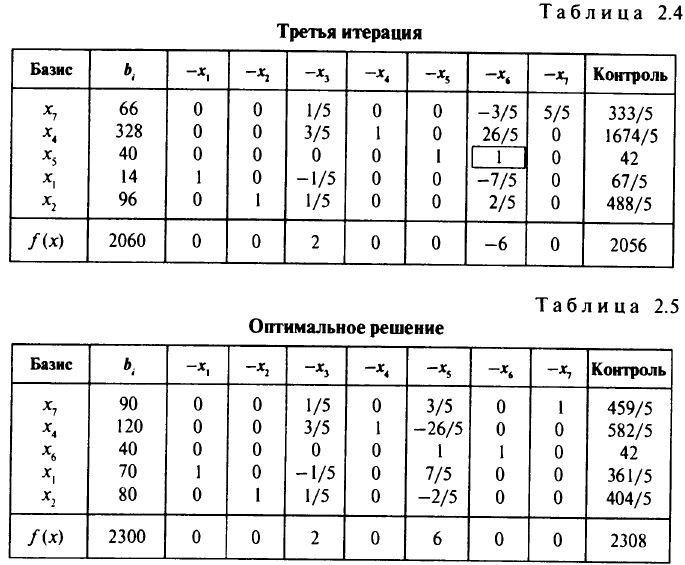
В табл. 2.5 все коэффициенты строки 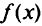неотрицательны, значит, максимум 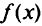достигнут и получено соответствующее ему решение:
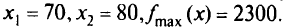
Таким образом, максимальная прибыль составит 2300 руб. при производстве 70 женских и 80 мужских костюмов. Слабые переменные оказались равными
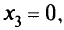
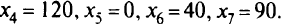
Что же они показывают? Значения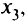 
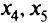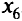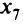показывают остатки ресурсов: шерсть и трудовые ресурсы израсходованы полностью, лавсана осталось 120 м; и показывают, на сколько перевыполнены плановые задания по числу костюмов и по прибыли (имеем в виду, что 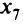= 90 • 10 = 900 руб.).
Замечание. Обратим внимание на тот факт, что в рассмотренной задаче оптимальное решение мы устанавливали по наличию неотрицательных коэффициентов в строке максимизируемой целевой функции, а в примере разд. 2.2 — по наличию неотрицательных коэффициентов в минимизируемой целевой функции. Здесь никакого противоречия нет: в нашем примере переменные указаны со знаком минус, поэтому и рассматривались неотрицательные коэффициенты.
Рассмотрим графическое решение этой задачи. Поскольку задача двумерная, то решим ее графически. Система ограничений-неравенств определяет многоугольник допустимых решений (рис. 2.3). Определим полуплоскости, задаваемые неравенствами-ограничениями задачи. Для этого построим прямые, заменив в ограничениях знаки неравенств на знаки равенств. Чтобы выяснить, какую часть плоскости описывает неравенство, подставляем в него пробную точку, например (0, 0), и устанавливаем, удовлетворяет ли она неравенству. Если неравенство удовлетворяется, то искомая полуплоскость включает точку (0, 0). В противном случае берут другую половину плоскости.
Для первого неравенства прямую
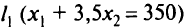
строим по точкам
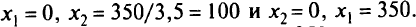
Пробная точка (0, 0) удовлетворяет неравенству 0 < 350, т.е. точка (0, 0) входит в искомую полуплоскость (она отмечена стрелочками у прямой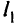 
). Прямую
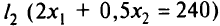
строим аналогично: при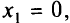 
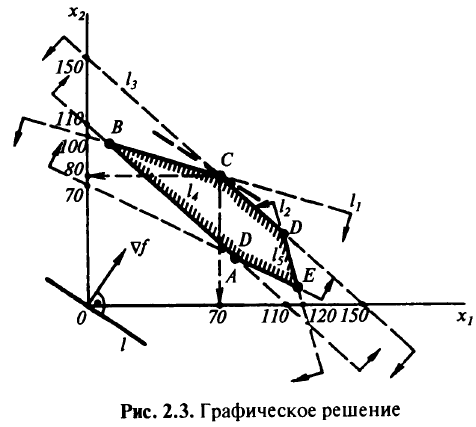
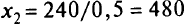и при 
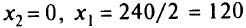. Точка (0, 0)
принадлежит искомой полуплоскости. Рассмотрим последнее неравенство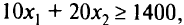 
, ему соответствует прямая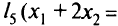 
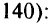: при 
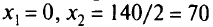и при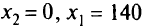 
. Точка (0, 0) не удовлетворяет неравенству 
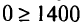(ложно), т е. надо взять полуплоскость, не содержащую точку (0,0). Пересечение полуплоскостей дает выпуклый многоугольник 
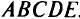. Для нахождения максимума функции 
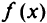надо построить линию уровня. Пусть 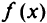= 0, тогда уравнение линии уровня 
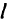будет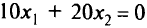 
— прямая, проходящая через начало координат параллельно прямой 
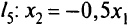. Градиент целевой функции 
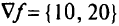показывает направление ее возрастания. Прямую 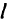перемещаем параллельно самой себе в направлении 
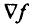до тех пор, пока она «не выйдет» из области 
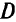. Получаем точку 
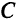, которая является точкой пересечения прямых 
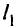и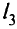 
:
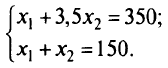
Решая полученную систему уравнений, находим оптимальное решение, т.е. координаты точки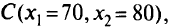 
и вычисляем максимальное значение целевой функции
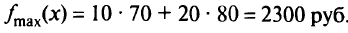
Замечание. Допустим, что в рассматриваемой задаче требовалось найти минимум целевой функции
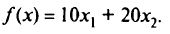
В этом случае линия уровня «вошла» бы в область по линии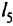 
, т.е. все точки отрезка 
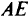являлись бы оптимальным решением (бесчисленное множество решений).
Эта теория взята со страницы лекций по предмету «математическое программирование»:
Предмет математическое программирование
Возможно эти страницы вам будут полезны:
