Обоснование последовательности расчета
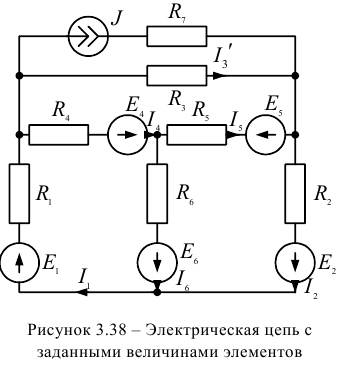
На рисунке 3.38. представлена электрическая цепь с заданными величинами сопротивлений резисторов 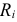 и величинами
и величинами 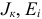 .
.
В задачах анализа электрических цепей необходимо выполнить расчет величин токов в ветвях электрической цепи.
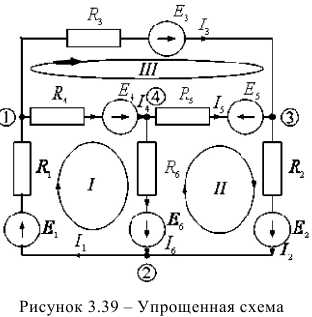
На первом этапе целесообразно произвольно выбрать направления токов в ветвях, упростить цепь, применив замену источников тока на источники ЭДС, где 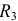 может служить внутренним сопротивлением модели реального источника энергии, состоящего из источника тока
может служить внутренним сопротивлением модели реального источника энергии, состоящего из источника тока 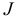 и резистора
и резистора 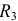 .
.
Резистор 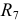 на рисунке 3.39 отсутствует, т.к. он подключен последовательно с бесконечным сопротивлением источника тока
на рисунке 3.39 отсутствует, т.к. он подключен последовательно с бесконечным сопротивлением источника тока 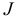 . Последовательно с резистором
. Последовательно с резистором 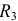 в схеме (рисунок 3.39) появляется ЭДС
в схеме (рисунок 3.39) появляется ЭДС 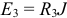 .
.
Так как метод непосредственного применения законов Кирхгофа состоит в составлении необходимого и достаточного количества уравнений по первому и второму законам Кирхгофа и дальнейшему их решению, на втором этапе необходимо подсчитать количество ветвей, и следовательно, неизвестных токов 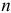 и количество узлов
и количество узлов 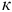 , пронумеровав их. Для рисунка 3.39
, пронумеровав их. Для рисунка 3.39 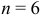 и
и 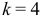 .
.
Если составить уравнения по первому закону Кирхгофа для всех узлов схемы, то в полученную систему уравнений каждый из токов войдет дважды, но с различными знаками. Если сложить уравнения, то полученная сумма будет равна нулю, что указывает на взаимную зависимость полученной системы уравнений.
Для цепи, изображенной на рисунке 3.39, например, система уравнений, составленных по первому закону Кирхгофа, для всех узлов при положительном выборе знака токов, отходящих от узла, имеет вид:

Сумма всех уравнений в системе (3.25) равна нулю, а сумма только трех любых уравнений приводит к уравнению исключенного узла.
Поэтому, количество независимых уравнений, составленных по первому закону Кирхгофа, на единицу меньше количества узлов к. Для данной цепи 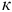 -1=4-1=3.
-1=4-1=3.
На третьем этапе необходимо составить по второму закону Кирхгофа недостающее количество уравнений для независимых контуров:

Независимые контуры должны отличаться друг от друга хотя бы одной новой ветвью.
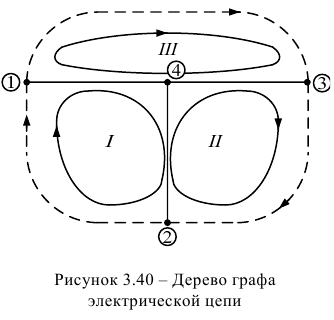
Для выбора независимого контура можно использовать любое дерево графа цепи, дополняя его последовательно ветвями соединения (пунктирные линии). На рисунке 3.40 представлен граф заданной электрической цепи, изображенной на рисунке 3.39.
Независимые контуры показаны на рисунке 3.40. Направление обхода контуров выбрано совпадающим с направлением тока периферийной ветви, входящей только в один контур.
Для выбранных контуров и направлений обхода элементов система уравнений по второму закону Кирхгофа будет иметь вид:
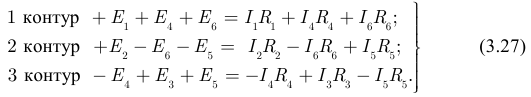
В четвертом этапе решаем общую систему уравнений (3.25), (3.27) подстановкой, без уравнения для четвертого узла, можно найти все токи данной цепи, а величина тока 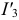 (рисунок 3.38) может быть найдена по уравнению
(рисунок 3.38) может быть найдена по уравнению 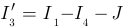 .
.
Пятый этап посвящен проверке величин вычисленных токов как по выполнению исходных уравнений (1), (2), так и по уравнению баланса мощностей. Уравнение баланса мощностей для примера цепи на рисунке 3.39 имеет вид:
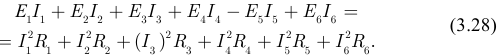
В левой части уравнения (3.28) мощности могут быть как положительными (в режиме генератора), так и отрицательными (в режиме приемника).
Эта страница взята со страницы задач по электротехнике:
Электротехника — решения задач и примеры выполнения заданий
Возможно эти страницы вам будут полезны:
