Метод наименьших квадратов нахождения приближенной функциональной зависимости двух переменных
Пусть на основании наблюдений требуется установить функциональную зависимость показателя 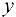 от фактора
от фактора 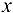 :
:
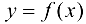
Пусть в результате наблюдений получено 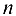 значений
значений 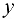 при соответствующих значениях фактора
при соответствующих значениях фактора 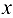 , табл. 24.1.
, табл. 24.1.
Таблица 24.1

Вид функции (24.1), называемой функцией регрессии, устанавливается или из теоретических соображений, или на основании характера расположения на координатной плоскости точек, соответствующих результатам наблюдений (поле корреляции).
При выбранном виде функции 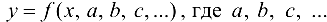 — неизвестные параметры, остается подобрать их так, чтобы в каком-то смысле функция наилучшим образом описывала рассматриваемый процесс.
— неизвестные параметры, остается подобрать их так, чтобы в каком-то смысле функция наилучшим образом описывала рассматриваемый процесс.
Широко распространенным методом решения данной задачи является метод наименьших квадратов (МНК). Рассмотрим сумму квадратов разностей значений 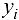 , полученных в результате наблюдений, и функции
, полученных в результате наблюдений, и функции 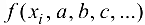 в соответствующих точках:
в соответствующих точках:
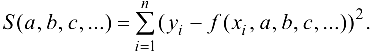
Подберем параметры 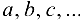 так, чтобы эта сумма имела наименьшее значение. Таким образом, задача сводится к нахождению таких значений параметров
так, чтобы эта сумма имела наименьшее значение. Таким образом, задача сводится к нахождению таких значений параметров 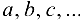 , при которых функция
, при которых функция 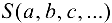 имеет минимум.
имеет минимум.
На основании необходимых условий экстремума ФНП получаем, что значения параметров 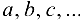 должны удовлетворять системе уравнений
должны удовлетворять системе уравнений
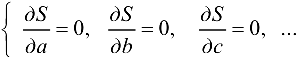
или
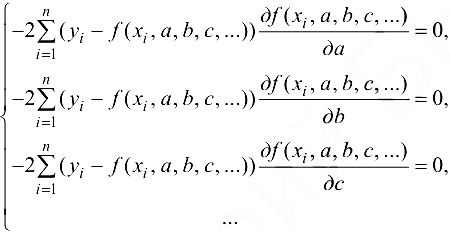
В системе (24.3) уравнений столько, сколько неизвестных параметров имеет функция (24.2).
Заметим, что вопрос о существовании решения системы уравнений (24.3) и существовании минимума функции (24.2) исследуется в каждом конкретном случае в зависимости от вида выбранной функции 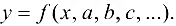 .
.
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:

