Оглавление:

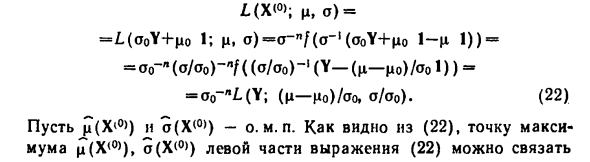



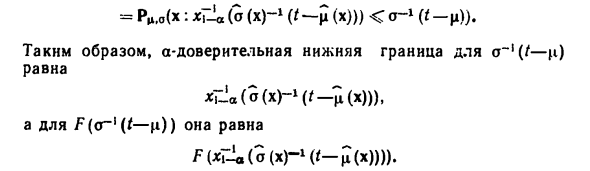
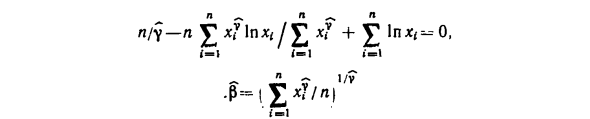


Метод Монте-Карло в модели сдвига-масштаба
- Рассмотрим статистическую модель, определенную в n измерениях Плотность семян f {x; u, o) -o — «/. (o — ‘(x-th-1)), 1 = A 1), B0) Где f (x) -f (x; 0, 1) является определенной известной плотностью. Неизвестный параметр. Модель B0) Пример применения цензуры при наблюдении Доступная статистика заказов в Эквивалентная плотность наблюдений (см., Например, (VI) §16) Мой и. ° с = — ^ T F M Где F (t /) — φ. r плотность f (т /). Это так называемая цена типа II Цензура, модель B0) включает цензуру I типа.
Интервал (t, s) (см. [9, §6.3]). Покажите, как выбрать с помощью искусственного моделирования Для образца с плотностью f (x) Параметры с и а. Исходить из. Т. Пл. (Х), а (х), но Этот метод может быть применен к любой оценке μ, o. Я съел раздачу. с. ) -J), er » (X), B1) Плотность распределения X составляет B0), Показано совместное распределение параметра ель. с. B1) Он не зависит от параметра q, но для q (x) и (x) -o. Метро Fixy- Изменить значение CO | oo параметры μ, a, X (C> является случайным Образцы плотности f (x; z0, oo), Y = o -co ), являются стандартными
Были соблюдены значения а-а), которые соответствуют известным интерфейсам. Людмила Фирмаль
Стандартный случайный вектор плотности f (y; 0, 1) = f (Y). по-видимому И а) = L (aoY + no 1; i.a) = a — «/ (a — ‘(oo? + Q0 1-q 1)) = = a0-I (o / a0) -LD (a / ao) -1 (Y- (t-d0) / o01)) — (U_Mo) / 0o, a / a0). B2) mp th (X @>) и a (X @)). Как видно из B2), максимум До μ (X <0>) и (X <°>) слева от уравнения B2) 207 Максимум функции L (Y; q ‘, a’), равный q, ‘= » =? (Y), d ‘= a (Y). просто ao- (M (X <°) -Mo)) = M (Y), ao-a (XC)) = a (Y). B3) Поэтому эл.в. B1) соответствует распределению Распределение диеты. с. n (Y), «a (Y), если необходимо. Для приблизительного численного расчета совместного распределения Распределение вероятностей H (u, o) = ^ (u (?) , B4) По плотности / Y (i) (y) = / (y; 0,1), 1 = 1, …, NB4) Последовательность из N независимых тестовых пар была съедена. , : В (M (Y)), a (YO)), i-l N, B5) И ф. р. H (u, v), где e рассчитывается. е. р. HN (U, V) и положить H (u, v) <HK (u, v).
В результате получаю с помощью B3). Rts.a (x: <r ^ a (x) <a) = H1 (k) в HAA (, + bo), P ^. (X: a (x) -1 (q (x) -c) <r) = P ^. (X: (q (x) -u) a- ^ (x) -1a <v) = » где G (u) = JJ A (x, y) dx dy; A (x, y) = d * // (x, 1 Таким образом, доверительный интервал для a и q имеет вид a (x) / (x, _ «/ 2 (// J) -1 <a <a (x) / (xa / 2 (Я ^) — 1, B6) q (x) -a (x) x, _a / 2 (G) <u <q (x) -9 (x) xa / 2 (G), B7) Где xa (// |) и xa (G) обозначают соответствующий квантиль Распространение. Знание совместного распределения оценок q и a Рассчитать доверительные интервалы для любой пары Параметрическая функция φ (μ, α). В частности, 208 Речь идет об одномерной итеративной (цензурированной) выборке е. р. F (a ~ l (x-µ)), где F (x) — известное φ. г показывает, как Доверительный интервал для Где т фиксируется. Учитывая монотонность функции F Достаточно построить альфа-доверительную границу <p / (μ, <•) = *. = crl (т-т), потому что
- Для простоты рассматриваются только верхние альфа-устойчивые гра Border. Используя B3) d ‘° v’ o a (x) a a (x)) = Po, | (x: σ-1 (/ -μ) a (x) -1-µ (x) b (x) -1 <s). B8) Put Po ,, (x: тогда (x) -1-μ (x) a (x) -1 <s) -Qx (s). B9) B5) сила в соответствии с результатами моделирования. е. р. Q, .. v (s), Qx (s) ^ Q ,, y (s). Используйте f. р. Qx (s) <pf (|., a) = a до l (t-μ) любой /. Отклонение от принятой спецификации В обозначениях квантиль распределения Q обозначается через x (m). Порт захода (X: ta (x) -1- (X) b (x) <x, _n (t)) — 1-а. C0) Из B9), поскольку функция Qt (s) убывает относительно m,
Следовательно, функция y = Xi-a (x) возрастает относительно m. Кости такие, что Qx (s) непрерывны и строго монотонны по m Функция y = Xi-a (i) является обратной m = x ~ -a (y) -отношением Получи В8) и С0) 1-a = Rd .. (x: a (x) -1 (G-z (x)) <n, _a (a (/ -z))) = = P «, o (x: xT-la (a (x) -1 (t-t (x))) <a-1 (t-u)). Следовательно, нижний доверительный предел a равен » (/ -μ) равных ^ (Og-1 ^ -ц))
.: С преобразованием V, = 1N, выборка из распределения Xx X „ f «.i (x) преобразуется из распределения в выборку Yu …. Y„. Для P (a ~ 1 (y- \ x)) и q-E o = y ~ \ F (y) = l-exp (-expy) (См. Статью 1 § 4). Таблица расчетов для Томана, Бэйна, Антла * ‘ Построить разные n и несколько доверительных интервалов Некоторые варианты цензуры. Мы используем их пример Числовые тестовые данные *
Эта техника проиллюстрирована в примере повторной выборки Из распределения Вейбулла f p Людмила Фирмаль
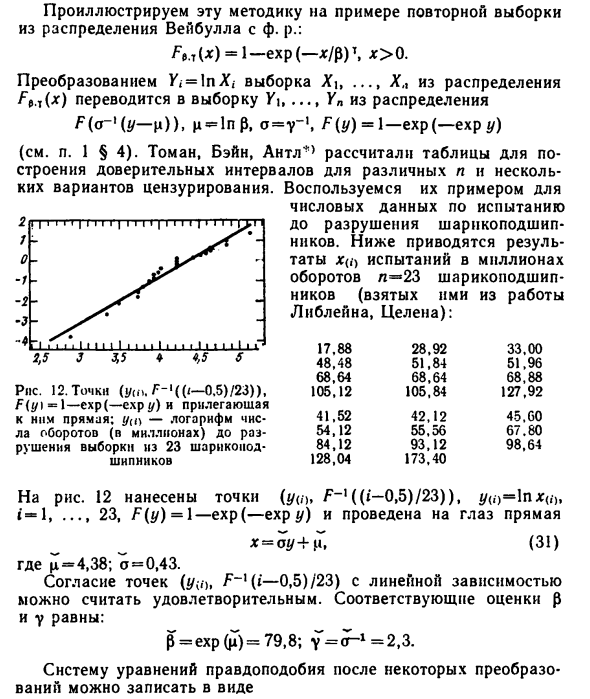
Пока шариковый подшипник не разрушен ^ Ник. Результат В общем / ^ -tats * <, •) миллионы тестов -i \ -jr \ rpm l = 23 шарикоподшипник- Шариковые подшипники (взяты с работы Liblane, Celena): -2 т 5 Rns. 12.Points (ya \ .F ~ l ((i-0, $)! 23)), F (y \ = 1 — exp (-exp) и соседи Прямо к ним. прж-чис логарифм До скорости вращения (1 миллион единиц) 23 шаровидной деструктивной выборки Шариковый подшипник 17,88 48,48 68,64 105,12 41,52 54,12 84,12 128,04 28,92 51,84 68,64 105,84 42,12 55,56 93,12 173,40 33,00 51,96 68,88 127,92 45,00 67,80 98,64 На рисунке 12 отмечены точки (* / <,,, F ~ l ((i — 0.5) / 23)), j / (,, = ln * <, • ,, i = l, … 23, F (y) = l — exp (-exp y) и прямые линии нарисованы на глаз
Где ^ = 4,38; а = 0,43. Точка (y ^, F ~ l (i-0.5) / 23) и соглашение о линейной зависимости Можно считать удовлетворительным. соответствующая оценка р И равных: p = exp (q) = 79,8; f = ir- * = 2,3 Система некоторых преобразованных уравнений правдоподобия Преобразование может быть записано как n / y-nYxY \ nx (/ Yx? + л л 1 / V 1 = 1 •) Technometrics, 1969, v. 11, стр. 445-560; 1970, v. 12, стр. 363-371. автор То есть «противоположность» была использована. NZ ! И nfiuiero подход, и зависит от частного
Свойства распределения Вейбулла. 210 Численное решение приводит к значению Y = 2,102; (f = 81,99. Напишите квантили распределения ели. с. v / v = @ / 0) «» ‘Рассчитано Томаном и др. с использованием метода Монте-Карло » > V a P> ч 22 24 0 0 0 02 0,752 0,759 0 0 0 +0,05 0,798 805 0 0 0 10 0,843 848 0 1 1. 90 320 301 0. 1 1 95 418 392 0 1 1 96 583 504 найти доверительный граф с помощью линейной интерполяции по n а = 0,1 лет границы: 1,50 = Y / Xi-e / 2 <Y <? / ** 2-2,62.
Запишем некоторые значения квантильного распределения xa e.v. Рассчитано Томаном, но 22 24 0.02 -0,509 -0,483 0,05 -0,404 -0,384 Другие: 0 -0 -0 +0,10 314 299 0 0 0 0,90 302 288 0 0 0 +0,95 398 379 0 0 0 98 519 494 найти доверительную границу линейной интерполяцией по n Для а = 0,1 р: 68.04 = ¦-p exp (- * i_a / 2 / Y) <p <p exp (- * a.2 / y) = 98.76.
Смотрите также:
| Функция правдоподобия | Проверка статистических гипотез |
| Оценки максимального правдоподобия | Лемма Неймана—Пирсона |
Если вам потребуется заказать статистику вы всегда можете написать мне в whatsapp.

