Оглавление:













Метод механического импеданса
- Метод механического импеданса позволяет быстрее и проще вычислить стационарное движение линейной системы, подверженной гармоническим возмущениям, по сравнению с классическим методом интегрированием дифференциальных уравнений движения.Применимо к линейным системам с 1 и несколькими степенями свободы. Прежде чем мы объясним суть метода, приведено краткое описание векторного представления гармонических величин. Рассмотрим вектор Z определенной длины, Z, который возникает из начала координат и вращается с постоянной угловой скоростью, в сложном случае.
Проекция на действительную ось x и мнимую ось y оси вектора всегда равна, OP X f Z cos at, 1 OQ 0 Zsin oi 2 Является гармонической функцией амплитуды Z и окружности. Сам вектор Z может быть представлен в виде числа компа в виде треугольника или экспоненты. З з с COS о Zsin о0 Зе. 3 частота Лекс Переход от одной формы к другой основан на общеизвестном Официальный Эйлера ei0 cose Zsin 8. В настоящее время функции 1 и 2, описывающие гармоническое движение, могут быть представлены в виде действительных и мнимых частей коэффициенты I функции 3. .в З Ре зэ, 4 J В Им Зэ. 5 В данном случае отношения 6 И вы можете сделать это сами. 7 Точно так же 8 9 д. С Зе зе зе о Зе к Зе —О З и т.
Действительно, применив эту теорему, мы определим уравнение траектории, скорость и ускорение центра тяжести твердого тела. Людмила Фирмаль
По-видимому, каждая производная вектора Z имеет поворот на 90 градусов против часовой стрелки с умножением w на ее длину.18л рисунок Представлен вектор Z и его 1-я и 2-я производные 0.7. В более общих случаях форма вектора Z имеет вид З Зэ — 10 Имея в виду взаимосвязь, полезно ввести понятие комплексной амплитуды Z. Ze1 и — Зе, ielai Зелал. Так как из 11 11 Z Ze , y Z 1, 12 13 Тогда действительная амплитуда Z равна модулю комплексной амплитуды Z. При решении задачи часто приходится рассматривать несколько векторов с одним и тем же вектором, вращающимся вокруг начала координат. Угловая скорость w естественно, в этом случае только их относительное положение равно important.
Соответствующая векторная диаграмма строится с одной фиксированной точкой, например 1 0.Положение вектора в момент времени 0 10 совпадает с положением вектора, представляющего комплексную амплитуду 12. Из алгебры известно, что сложение и вычитание более 2 комплексных чисел равно сложению и вычитанию числа этих чисел. vectors. So, при добавлении вектора, вращающегося с одинаковой угловой скоростью, можно использовать правила параллелограмма. Однако на этом аналогия между комплексными числами и векторами заканчивается.
Таким образом, умножение комплексных чисел и умножение векторов-это совершенно разные операции, а деление комплексных чисел в векторной алгебре вообще не соответствует никаким операциям. При решении линейного дифференциального уравнения вводится комплексная экспоненциальная функция вида Гармоническая функция вида Z cos rat-y или Z sin rat-y , как правило, значительно упрощает расчет и очень удобна. Используются следующие важные теоремы Линейное уравнение. … ВФ 0 Если существуют вещественные коэффициенты a и F Fi ZFs, а F и Ft также вещественны, то решение будет комплексным. x x1 Zx11 и xv и xt являются решениями уравнения в правой части 14.Равны B и FT соответственно.
Метод механического импеданса основан на этой теореме и том факте, что стационарное движение линейной системы, подверженной гармоническому возмущению частоты w, описывается гармонической функцией той же частоты m. So … Чтобы определить это движение, достаточно найти соответствующее ему. Комплексная амплитуда. Рассмотрим общий случай линейных систем с 1 степенью freedom. It поглощает возмущающее действие синусоиды рис. 18.5.Точка O указывает положение статического эквивалента.
T будет постоянной функцией. Измеряется координата x массы m, из которой жесткость пружины обозначается буквой c, а постоянная демпфера пропорциональный коэффициент — буквой A. движение рассматриваемой системы МДж — — аз — — СХ ФСИН по. 15 Введем комплексную силу возмущения F Fe. 16 Очевидно, что фактическая сила заклинивания Fslnerf Им 17 Установившееся движение системы происходит на той же частоте, но только фазовый угол отстает от возмущения. Таким образом, комплексные координаты описываются в виде 10 Х Хе 18 Тогда, исходя из сформулированной выше теоремы, фактическое смещение равно х 1хх Xtin е -Пхи.
Поэтому расчет установившегося движения системы сводится к определению комплексной амплитуды перемещения X Xe — 9.Это эквивалентно нахождению суммы. 20 Для этого используйте комплексную функцию справа от равенства 18 и выразите ее в виде Xe A1.Найдите 1-ю и 2-ю производные по времени t X не зависит от времени и замените эти величины на левую часть уравнения движения 15 вместо каждого из x, x и соответственно, правая часть уравнения-Fe, Al.
Затем после сокращения в e СКО-яко1 21 Зная комплексную амплитуду 21, можно легко описать формулы для действительной амплитуды X и фазового угла с помощью формулы 20.У нас есть С-что ал г с-потом 1 1 АВ 1 22 Модуль частного равен частному модулю арг — — — argZ, где z-любое комплексное число. Подставляя найденные значения X и p в уравнение 19, находим стационарное движение системы. При решении конкретной задачи с использованием численных данных нет смысла использовать готовые формулы 22 и 23. в этом случае их следует запомнить. Лучше, выполнив все вычисления, найти комплексную амплитуду X, а затем определить модуль и аргументы полученного числа.
Если сила возмущения задана в виде F cos w , то вместо 17 Ф потому что ш Ре Ф, 17 И вместо 19 Х ф — Рекс Xcos ВЗ — Ф. 19 Все остальное не меняется. Триплетации lao-mo , которые стоят в знаменателе формулы 21, называются полным импедансом учитываемой колебательной системы, а величины — тогда, 1ao и с-импедансами элементов массы, демпфирования, упругости. Таким образом, импеданс упругого элемента равен упругой постоянной этого элемента, импеданс демпфирующего элемента равен коэффициенту затухания, умноженному на 1, а импеданс массового элемента равен массе, умноженной на −1.Общий механический импеданс системы общее механическое сопротивление будет равен сумме импедансов ее элементов.
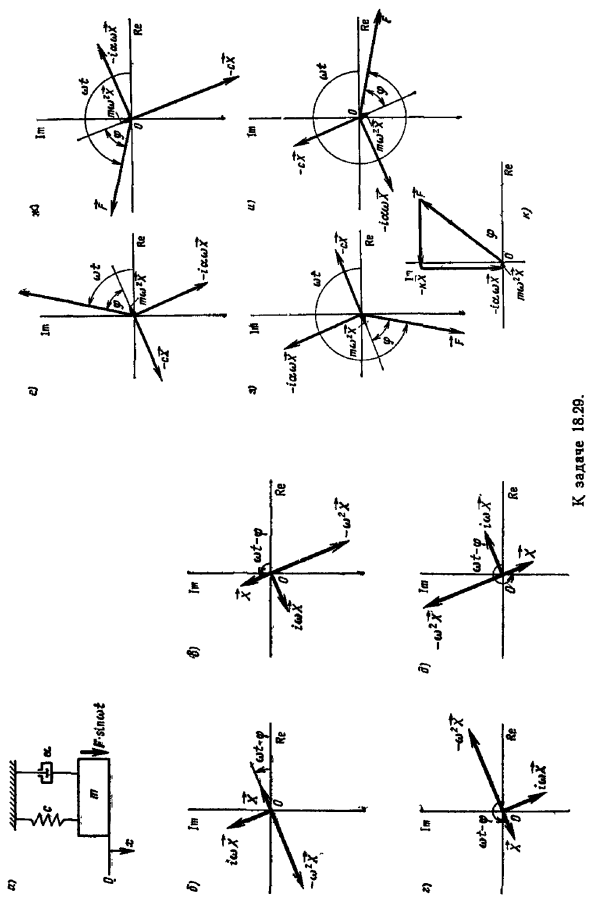
Обратите внимание, что размер механического импеданса определяется как сила, деленная на перемещение. Электротехника использует аналогичную концепцию электрического импеданса. Задание 18.29.Уравнение движения системы, показанное на фиг. TX cut-trcx F 1 Если рассматривать это уравнение как уравнение равновесия сил, основанное на принципе Даррена Бейла, то эти силы выражаются в виде векторов вращения. Определить положение вектора, если 1 масса m движется вниз и находится ниже положения статического равновесия О 2 масса m поднимается, но опускается ниже точки статического равновесия O. 3 масса m движется вверх и находится за пределами точки статического равновесия O.
Масса m движется вниз, но выше точки статического равновесия O. In во всех этих случаях график показывает, что Формула 1 выполняется. a 300 кадров в секунду s 600 Н м F 50 Н o 2 рад с Решение. При создании векторной диаграммы требуются величина амплитуды смещения X и фазовый угол. Для Ф 1л З1 По вопросу 18.29. Для их расчета непосредственно используются формулы 22 и 23.У нас есть Ф. Н Пак и К С-М О а о С00-10-2 300-2 2 Ф 3 rctgd b arctg 50 10-2 916 рад-5Г30 — Рисунок B векторы смещения х, налоговые скорости и ускорения — w5XX отображаются для 4 государств массы m, которая обозначается состояние проблемы.
На самом деле, в случае 1, например, перемещение и скорость массы является положительным, потому что это вниз, а ускорение отрицательно, т. к. это вверх. В этой задаче, х 1хх, х им йех и X им —г х, так что рисунок в точности совпадает это состояние системы. Точно так же можно увидеть и рисунок. C, d, E статус 2, 3, 4. При построении диаграммы сил необходимо учитывать следующее упругая восстанавливающая сила СХ пропорциональна смещению х и всегда противоположна по знаку. Демпфирующая сила оси пропорциональна скорости и направлена в противоположную сторону. Наконец, сила инерции TX пропорциональна ускорению и снова противоположна направлению.
Таким образом, векторы, соответствующие этим трем силам, будут равны — cX , — iaaX и m X. расчет длины прост — CX cX 500 0.066 33 Н — ashX 300 2 0.066 39,6 Н tchAh mxrX 10 2 −0.066 2.64 i. Используйте эти данные и кинетическую диаграмму рисунка, чтобы создать силовую диаграмму всех 4 состояний систем b, c, d и E. Е, Ж, З, и. Сумма векторов равна нулю, поскольку 4 силы, отображенные на каждой диаграмме, находятся в равновесии. То есть она должна быть закрытой Polygon.
- Достаточно построить только 1 такой многоугольник ввиду того, что фигуры E, g, h отличаются друг от друга только углом поворота относительно координатных осей. На рисунке K силовой полигон построен со временем t p w, поэтому он будет w — p 0.В противном случае этот многоугольник будет вращаться как фиксированное целое число под определенным углом относительно начала координат. На рисунке показано, что силовой полигон замкнут. Таким образом, формула 1 выполняется во всех случаях, указанных в рассматриваемом условии. Задание 18.30.Движение колебательной системы описывается уравнением О ах СХ Потому что ВЗ г.
Механический импеданс определяет установившееся движение системы. Решение. Комплексное число вместо действительной силы возмущения Fcos cot-f-y А Р. Очевидно. Ф в COS со г Ре 2 Запишите комплексное смещение с учетом равенства частот и фазового запаздывания в виде Х Хе ТФ Хе X Xe-1 — комплексная амплитуда смещения. Комплексная скорость А сложные ускорения равны — co да s w o da t. Формула вместо IX, действительная сила возмущения, смещение, скорость, ускорение, соответствующие комплексные величины вместо — та 1аа с Хе ас п Фэй ал ж.
Задачи динамики поступательного движения твердого тела решаются посредством теоремы о движении центра инерции системы материальных точек. Людмила Фирмаль
Для уменьшения с Л1 да- —— с-Ма icua Из последнего соотношения определим амплитуду установившегося колебания Ф В С-му Сио 3 Фазовая задержка Р — арг arctg-з — СР 4 Сравните с формулами 22 и 23. С учетом соотношения 2 опишем уравнение установившегося движения системы в виде X 0 Re X x cos erf y-q , X и определяются равенством 3 и 4. Задача 18.31.As показанная на рисунке машина весом 225 к установлена на пружине и демпфере. Суммарная жесткость пружин составляет 17 550 I W. суммарный коэффициент затухания 350ya-seya F.
Точка O соответствует положению статического равновесия. При приложении к машине возмущающей силы 88 cos 351 Н механический импеданс определяет установившийся отклик системы. Решение. В зависимости от состояния задачи, m −23 кг, a 350 нсек м s 17 550 Н м F 88 н, w 35 рад с Вычисляет полное механическое сопротивление системы. с — яй 1ash 17,550 —23-35 1.350-35 −10620 112 250 г 10 620 12 250 е ре, ГВ о 16 200 — 5У. Согласно формуле 21, комплексная амплитуда смещения равна L2to -. gr-0.0054 — это так.
Фактическая амплитуда колебаний Х 0.00543 я 5.43 яму Фазовый угол равен Р −0.855 рад −49 Поскольку возмущения силы Косинус, смещений описывается следующим образом х Т со х коэф- п Или наконец-то х 1 0.00543 со 351 0.855 я. Задание 18.32.Создайте уравнение движения для системы, показанной на рисунке. а, и метод механического импеданса определяет установившееся движение этой системы. Решение. На рисунках b и c показаны силовые схемы массы m и демпфера A соответственно. Исходя из первой схемы, опишем уравнение движения массы М. МЗ а а-й СХ С х-Х 0 Подставляя заданное синусоидальное смещение на ХХ дает мб а — а с СХ х cxa от xinerf. 1 Демпфер а и пружина с соединены последовательно.
Таким образом, демпфирующая сила будет равна напряжению пружины. а л-ла с ХС 2 Вы можете исключить координаты демпфера из этих выражений, подставив их вместо этого в Формулу 1. его значение взято из a I- 2 с Решите полученное таким образом уравнение относительно xt. mH ctxt c cx x cxxx sin at, откуда ХL — clX1sinat-Тх — с с х. 3 Дифференцируя уравнение 3 по времени и подставляя результат 1, получаем мн е cXlx потому-мн- с х С С1 ки isln Или после простого преобразования I Aje fca 2 x Xlcos Bi Xxsin at 4 поэтому движение рассматриваемой системы является системой уравнений 1 и 2 или уравнением 1-го-3-го порядка 4.
Форма правой части Формулы 4 представляет собой cmat — — Bsiaat, как известно, 1 гармоническая функция A cos at Bsin at Csin at a Где C 4 5 амплитуда, a arctan L fi — фазовый угол. Если мы перепишем правую часть уравнения 4 как единственную гармоническую функцию, мы можем применить метод механического импеданса к этому уравнению, чтобы найти стационарную реакцию системы. Однако этого может и не быть. Примените метод механического импеданса непосредственно к Формуле 4 2 раза. Каждый проход оставляет один из 2 терминов на правой стороне.
Так как уравнение 4 линейно, то сумма найденных в этом методе решений дает искомую стационарную реакцию системы, основанную на принципе суперпозиции принцип суперпозиции решений. Есть и 3-й способ, но в данном случае он наиболее удобен. Мы придерживаемся этого. Примените метод механического импеданса непосредственно к системе уравнений 1 и 2. для этого введем комплексное возмущение c X 1 и опишем соответствующие комплексные перемещения в виде Xe 0 и X 01.Где X и A-комплексные амплитуды. Подставляя эти величины в уравнения 1 и 2, получаем систему из 2 линейных алгебраических уравнений относительно неизвестных X и X, после редукции на e.
Полученная система уравнений решается с помощью теоремы Крамера. Найти детерминанты системы Д х С — ПШ Ясень с Ясень в sh2, или после упрощения Д С, с — Яш Ясень с ХС- ышь. Детерминанты неизвестных X и X2 равны С1 1 а з А ас s1×1. Так… X — yX1 Ч-Наш Д — те эти c ci s, — ty3 iCKOCiXi — — — с, С ки-а а с —м Из последних 2 уравнений можно найти действительные амплитуды X и Xs и фазовые углы p и p8.
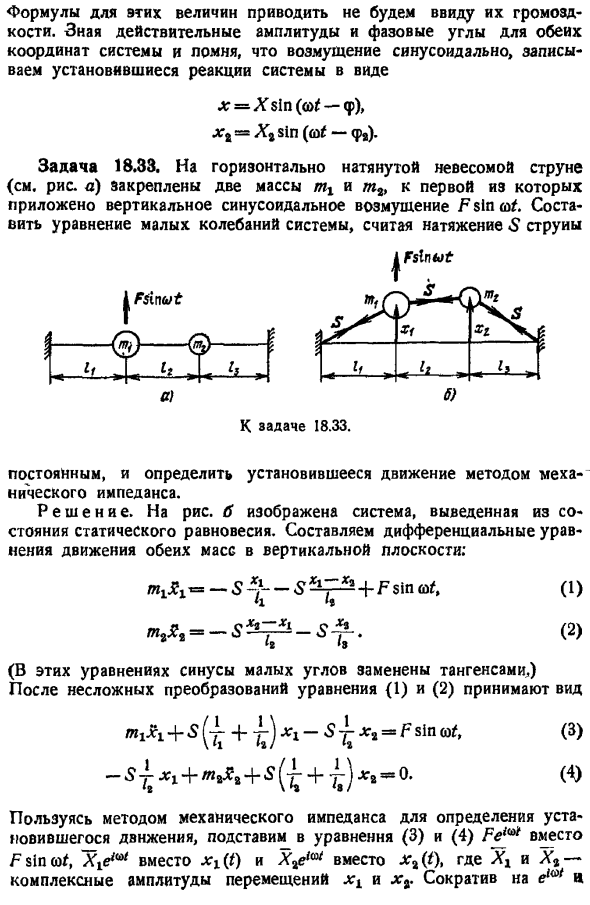
Ввиду громоздкости костей, формула этих величин не показывает. Зная действительную амплитуду и фазовый угол обеих координат системы, напомним, что возмущение является синусоидальным, запишем реакцию установившегося состояния системы в виде х Xsing Ми — п х ХВ грех Ми- 1. Задание 18.33.На горизонтально натянутой невесомой струне см. рисунок а сначала фиксируются 2 массы zhx и mit, а к ее исходной массе прикладывается вертикальное синусоидальное возмущение F sinmi.
Принимая во внимание натяжение струны S, Мы создаем уравнение для малых колебаний системы. .Fslnwt Шесть один Выпуск 18.33. Определите постоянное и стационарное движение методом механического импеданса. Решение. На рисунке b показана система, полученная из состояния статического равновесия. Создайте дифференциальные уравнения для движения обеих масс в вертикальной плоскости. 1 2 После простого преобразования уравнения 1 и 2 принимают вид ЗПР 5 л-с с FsinWi, 3 — slxi sd J — o. 0 Определите стационарное движение с помощью метода механического импеданса, заменив уравнение 3 и 4 Из на Ft вместо F sin at и заменив X вместо X, X вместо x 0 where и Xt .— Комплексные амплитуды перемещений xx и xt.
При преобразовании уравнения — си. Джей, с Л Л — , Х,-о. с Комплексная амплитуда Ai и Xt определяется из этих уравнений с использованием правил Крамера. Детерминантами системы являются Детерминанты неизвестного числа Xt и Xt равны соответственно Комплексную амплитуду можно найти следующим образом Отметим, что коэффициенты уравнений 5 и 6 являются действительными числами. Поэтому комплексные амплитуды и Хг X 1 в данном случае это действительное число. То есть фазовые углы pi и 2 будут равны нулю, если соответствующая комплексная амплитуда положительна, и 180, если отрицательна.
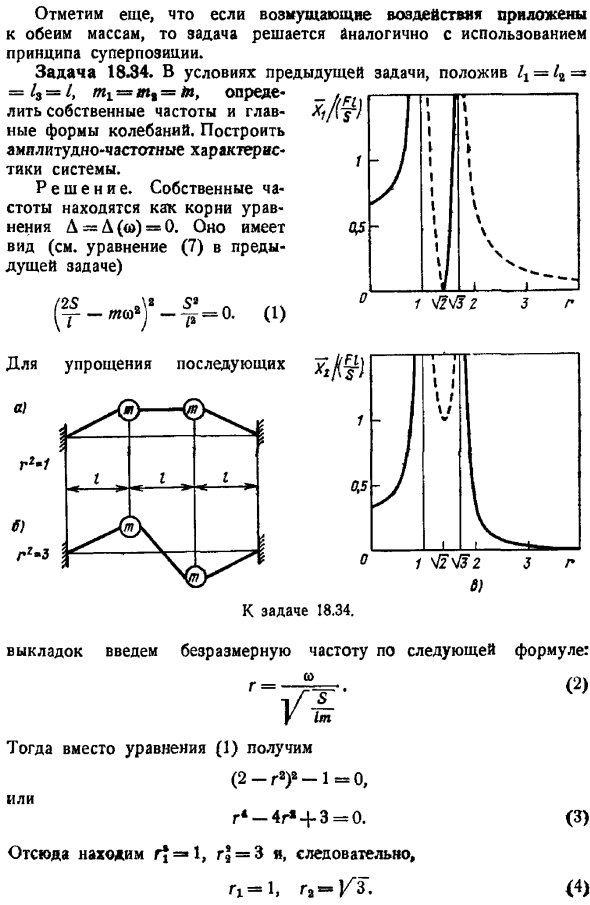
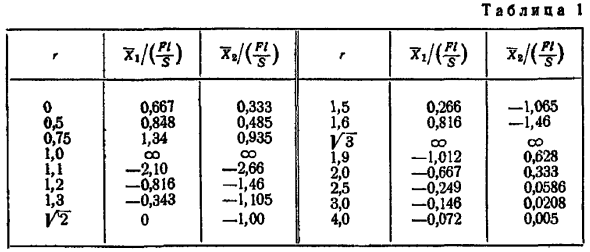
Поэтому, если колебания совпадают по фазе с возмущающей силой или наоборот, это описание применимо ко всем системам без демпфирования. Поскольку возмущающая сила синусоидальна, установившееся движение также синусоидально. ХL X1sin ОПН-ФД Х, Х грех — Где 1 X1, Aj Xj — фактическая амплитуда. Также отметим, что если возмущение относится к обеим массам, то задача решается также с использованием принципа суперпозиции. Задача 18.34.In условие предыдущей задачи, заданное 1r 1l a Расчет вводит безразмерную частоту следующим образом Тогда вместо Формулы 1 2-r −1 0 Р — 4г 3 0. Из этого следует, что r 1, rj 3 i.
Формула 2 3 4 Fl 2-g s R — 4r 3 Собственные частоты системы равны Комплексные амплитуды равны см. предыдущую задачу 5 6 И фактическая амплитуда I 2-g I s 4, s I- 7 8 I I 1 I 2 r — 4Р 3Р В формулах 7 и 8 под знаком модуля находится действительное число.
Смотрите также:
Предмет теоретическая механика

