Оглавление:





Метод медленно меняющихся амплитуд
Метод медленного изменения амплитуды. В электротехнике, беспроводной инженерии и других инженерных дисциплинах очень широко используется метод расчета переходных процессов, называемый методом медленно меняющейся амплитуды.
- Этот метод был предложен в 1921 году голландским физиком Ван дер Полем. Рассмотрим основы этого метода на примере нелинейного контура второго порядка
под воздействием периодических возмущающих сил. Людмила Фирмаль
Уравнение этой схемы описывается следующим образом: (B.14) Под действием периодической силы частоты o устанавливаются вынужденные колебания частоты w, а высшие гармоники выражаются слабо.
Известно об изучаемой схеме. Предположим, что искомая функция x (t) может быть выражена как: x = a sinω / b cosω /; (V. 15) где a и b — амплитуды желаемой вибрации, которая медленно изменяется со временем.
- Медлительность изменения a и b во времени обусловлена тем, что их производные по времени являются небольшими первичными величинами по сравнению с продуктами ya и (о, т.е. da db (B.16) dx-AND-SOY.
Чтобы принять это во внимание, dx da db 0 (0 cosω / -bto sinω / 4-sinω / -4-cosω / — sin co /. (B.18) Аналогично, вместо того, чтобы брать вторую производную этой формы, —co sin co / — + — sin co / 4 до dt2 dt dt dt 6 d? B da db 4 — COS co / 4 -cocosco / ——cosinco / -, d / 8 dt dt pr
вместо dt dt в качестве первого приближения Людмила Фирмаль
Мы игнорируем малый член второго порядка и оставляем малый член первого порядка. Это игнорируется в формуле -.dt Это потому, что потеря рассматриваемой схемы мала, поэтому амплитуда второго слагаемого в левой части формулы (B.14) является первой в левой части формулы (V.14).
Он относительно мал по сравнению с амплитудой 1-го и 3-го членов. Кроме того, в функции f (x) вместо x (B. 15) едва расширяет f (x) до dx Фурье, затем умножает ряд Фурье, представляющий f (x) на (правая часть уравнения B. 18) dx _ / (x ) — = Fo (a, b) 4-Fl (a, b) sin co / 4- (a ”b) cos ad 4- F3 (a, b) sin 2co / 4-d / 4-F4 (a, b)
Поскольку расчет cos 2co / 4 -… (B.20) основан на первой гармонике, постоянной составляющей A0 (a, b) и высших гармониках ряда Фурье (т. е. f3 (a, b) ), F4 (a, 6) J игнорируется ниже (Px — правая часть (B. 19) и использует формулу (B.14 вместо B вместо d dx fix)) -dt Fl Заменить (о * (sinω / — | -b cosω /) вместо (, b) sin (o / 4- (c, b) cosω / и coo .
Формула (B. 14) равна 2 Один из них — уравнение (B.21) — представляет собой уравнение коэффициента левого и правого уравнения sinω / x (B. 14), другой — уравнение (B.22) ) — левый и правый коско / коэффициент уравнения (B.14) Уравнение: db. «2co- + Fr (a, b) + a (co ‘-co2) = A; (B.21) (B.22).
Одновременные уравнения (B.21) и (B.22) Это два связанных дифференциальных уравнения, составленных из мгновенных значений медленно меняющейся амплитуды и b. В общем случае решение системы (Б.21) — (Б.22) может быть выполнено методом численного интегрирования или методом Волынкина.
В конкретном случае, когда внешняя периодическая сила равна нулю (A = 0) и функция Fl (a, b) = 0, система сводится к одному дифференциальному уравнению первого порядка: из производной da dt (B.23) Основные этапы перехода были рассмотрены выше Уравнение мгновенного значения (Уравнение (V. 14))
Медленно изменяющееся дифференциальное уравнение амплитуды. Этот метод может быть применен к другим более сложным уравнениям. , Термин слабый dx max / () — формула (B. 14) (и т. Д.), Один из которых соответствует максимуму оставшихся членов в формуле (B. 14), представляющих pa-a / d или
Напряжение активного резистора, dx и уравнение в нескольких цепях должны сохранять малый член первого порядка, игнорируемый выше: (/) = V a2 (/) 4-b2 (t) Пример 176. Решение для определения закона увеличения амплитуды колебаний напряжения на сетке трубчатого генератора § 239.
Решение. Уравнение для генератора вакуумных трубок было выведено ранее (уравнение (9.56 Повторите: анодный ток ia выражается через сеточное напряжение следующим образом: ^ ao + a-bf | по сравнению с уравнением (9.46), эталонная пунктирная кривая 255].
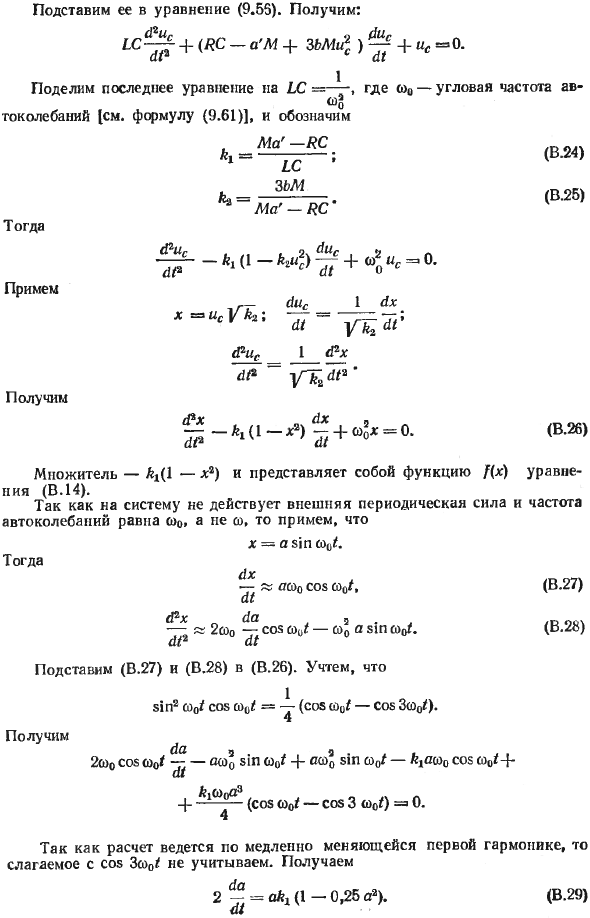
Подставим производную по времени по duc «уравнение di * (9.55). 1С ^ Г + (* с-Ч-We» 0. Разделим последнее уравнение на LC = -, где ω0 — угловая частота автоколебаний Да [см. Уравнение (9.61)], Ma ‘—RC_bn (B.25) * = Ma’-RC’ (B.24), d? Uc … 9. ^ Uc *> — * 1 (1 — +% «C = 0. dUc x» uc V k2; 1 dx dt до dt ‘1 I fe2 V 1 + s1e-k »
Согласно начальному значению амплитуды напряжения U’c, если / = 0, Uc == (ОДень 4а’М-RC U * C (Q_) ЗМЗ конденсатор на обоих концах Мгновенное значение напряжения «С = * Vсsin Wв ‘- ~ 2 d / RC sin (B.32) VI ч
Смотрите также:

