Метод максимального правдоподобия (ММП)

Метод максимального правдоподобия (ММП)

• Метод максимального правдоподобия (MMP) В классической модели линейной регрессии случайный член удовлетворяет Соответствует условиям Гаусса-Маркова, других проблем нет Критерием получения оценки коэффициента является минимизация суммы Квадрат отклонения.

• Этот выбор не был произвольным. Теорема Гаусса-Мара Кова имеет оценку наименьших квадратов Справедливо и эффективно как для больших, так и для маленьких образцов Условие Гаусса-Маркова выполнено. Однако в последних четырех главах регрессионная модель постепенно Коррелирует с условием Гаусса-Маркова, вдали от исходного значения Предпосылки.

Рассмотрено использование значений лага Переменная как переменная регрессии, примените нелинейную регрессию. Людмила Фирмаль

Анализ (например, оценка уравнений с использованием метода Кокрана-Оркатта), но Кроме того, я начал использовать инструментальные переменные. Метод оценки PI не основан на методе наименьших квадратов. Обоснование использования Метод IP дает согласованные оценки 350 Если они не даны методом наименьших квадратов, и если вы хотите минимизировать дисперсию распределения.

Если есть другие варианты, оценка является приемлемым решением. Однако поиск такого минимума не является главной задачей. К сожалению для простых любителей жизни В редком случае Гаусса-Маркова нет другого выбора, кроме как найти альтернативу наименьших квадратов Отображаются только те опции, которые принимаются.

Обычно различные исследования Владелец может предоставить несколько конкурирующих оценок. Каждый рейтинг Мы богаты. Например, для первой автокорреляции С упорядоченной и последовательной оценкой, Прайс-Винстен метод коррекции. Если бы вам пришлось выбирать Между этими двумя методами (хотя есть и другие)

Привлечение альтернатив и методов отбора, не упомянутых в главе 7 Будет интересно выбрать асимптотически верные оценки. Причина Соответственно, кран — метод Оркатта с коррекцией цены — Винстен Более желательный, чем метод Кокрана-Оркатта (и это было подтверждено экспериментально) Метод Монте-Карло), это вообще ты Оценки параметров Борокова имеют меньшую стандартную ошибку.

Вот момент перехода к оценкам с использованием метода максимальной истинности Сходство (ММП). Они обычно не спрашивают их Хотя это небольшой образец, Асимптотическое смещение обеспечивается при соблюдении определенных условий. Согласованность и асимптотическая эффективность. Кроме того, они обеспечивают Они предоставляют возможность для испытаний, которые не могут быть использованы в Для МНК.

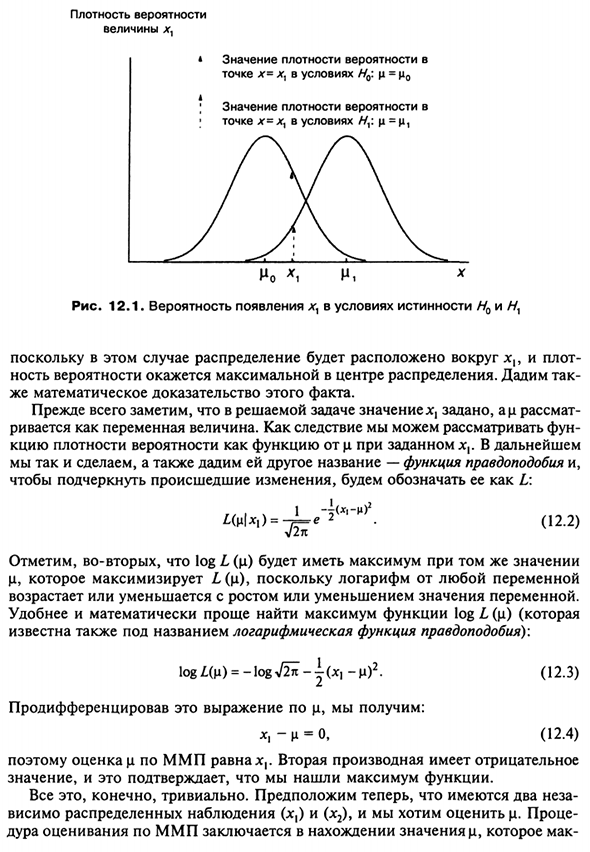
Что такое оценка MMP? Это может объяснить В простом примере. Предположим, что есть непрерывное случайное изменение Неизвестный средний JLI и известный стандарт (для простоты) Отклонение равно 1. Предположим, есть причина верить Переменная имеет нормальное распределение. И, наконец, Есть две альтернативные гипотезы: q = q0 и | 11 = | u1, и одно наблюдение x ,, Как показано на рисунке. 12.1.

Какую гипотезу вы выбираете? Принцип максимума Достоверность предполагает, что необходимо выбрать одну из следующих гипотез Наиболее вероятное событие. Потому что х это непрерывный сервис Чайная ценность, вероятность появления индивидуальной ценности Это бесконечно мало. Вместо этого сравните значения плотности х баллов {В случае двух гипотез, выраженных высотой функции Плотность вероятности.

Это ясно на рисунке. Функция 12,1 μ = μ 0 Высокая плотность вероятности в точке х. Следующий шаг — обобщение. Рассмотрим все возможности выберите тот, который дает значение fi и максимальную плотность Вероятность в х. Форма функции плотности вероятности переменной x с заданным q имеет вид / (X | Y = J * «‘(от A до C)’ (12,1)

• Задайте себе вопрос: какое значение q Конкретное наблюдение x,? Графически очевидный ответ: (i = x1? 351 Плотность вероятности значение chl * Значение плотности вероятности Точка x = xl в условии H0: q = q0 Значение плотности вероятности; • Точка х = х Y в условии //: c = c. Рисунок 1 2. 1. Вероятность появления chl в условиях истины H0 и / V,

В этом случае, потому что распределение размещено вокруг х, а плот Вероятность вероятности наибольшая в центре распределения. Вот так Это же математическое доказательство этого факта. Во-первых, обратите внимание, что в решаемой задаче значение x задается как a \ x. рассмотрение Используется как переменная.

В результате вы можете считать удовольствие. Людмила Фирмаль

Функция плотности вероятности как функция от q для данного JC, Затем дайте ему еще одну функцию вероятности имени, Укажите, чтобы выделить изменения, которые произошли Как L: Dt | x1) = — ~ = ^ «2 (D:,»)). (12.2) Затем обратите внимание, что log L (\ x) максимизируется с тем же значением μ. Максимизируйте L (q). Это логарифм переменной.

Увеличение или уменьшение в соответствии с увеличением или уменьшением значения переменной. Удобнее и математически легче найти максимальное значение функции log L (μ) (это Также называется функцией логарифмического правдоподобия) » войти! (| Li) = -logV2 ^ — | (x 1 -M) 2. (12.3) Дифференцирование этого уравнения по q дает: , -C = 0, (12,4) Поэтому c рейтингом. IMF равен x { Вторая производная отрицательна Значение.

Это подтверждает, что максимальная функция была найдена. Конечно, это все тривиально. Предположим, теперь есть два Независимо распределенные наблюдения (x {) и (x2). Я хочу оценить д. преимущества Глупость оценки МВФ заключается в нахождении значения q. Значение q Вводя частичную функцию плотности вероятности: (.I ,, Л (.1 f (xi, x2 \ i) = 4b. 2 (x, -z) ‘1 ™ < 2-C \ G2

Это выражение может быть преобразовано в логарифмическую функцию Я вероятности для данного х и JC2, и максимизация Как и прежде, мы устанавливаем функцию логарифмического правдоподобия: lQg ^) = -21ogV2J? -i (jc, -fi) 2-j (jc2-fi) 2. (12.6) Из этого выражения можно получить основное условие. (X1-q) + (x2-q) = 0, (12,7) Следовательно, оценка q по IMF равна (x, + x2) / 2. Этот результат не сложный.

Обобщать, когда есть n наблюдений. Оценка q по МВФ Примерное значение, соответствующее оценке по следующему методу: Малая площадь Когда МВФ применяется к классической модели линейной регрессии, предварительно Предположим нормальное распределение со случайными членами и оценим все коэффициенты Центы (не случайная дисперсия членов) равна полученной оценке С помощью OLS.

Поэтому из метода наименьших квадратов МВФ в этом контексте скорее эволюционная, чем радикальная Образование. Максимально допустимая в настоящее время логарифмическая функция вероятна Добиа выпускается практически всеми регрессионными диагностическими пакетами Статистика связана с результатами регрессионных расчетов.

Можно использовать Проверьте критерий отношения правдоподобия. Этот тест В следующем. Существует две версии модели, одна из которых является другой Добавить ограничения. Статистика 2 (LLU-LLR), где LLU и LLR -Лог-правдоподобная функция неограниченна и ограничена Каждая большая версия модели образца следует Распределение x2 с s степенями свободы при принятии нулевой гипотезы Точность ограниченной версии.

Где s — количество наложенных ограничений. (Подробнее об этом и двух других тестовых группах Отказ как часть максимальной надежности [тест Вальда и множество тестов Жители Лагранжа] П. Кеннеди рекомендовал работу [Кеннеди, 1985, с. 58- 59]. ) Тем не менее, в дополнение к теоретическим свойствам, принцип оценки параметров, Чтобы максимизировать потенциал этого образца, Привлекательный для эконометристов.

Принцип наименьших квадратов Конечно, есть преимущества, если выполняется условие Гаусса-Маркова, В противном случае все эти достоинства будут потеряны немедленно. Если ММП очень эффективный и привлекательный и очень адаптируемый Лен для тестирования, почему не всегда его использовать по существу 353 Есть четыре причины, почему нужно внимание.

Во-первых, это обычно доступно Граница особенно при анализе временных рядов Большая вещь И метод с желаемыми свойствами Большие образцы уступают другим методам маленьких образцов. один Фактический метод подтверждения для каждого конкретного исследования Эксперимент Монте-Карло.

Во-вторых, Такая популярная собственность поддерживается концепцией богатства Свойства и асимптотическая эффективность не являются безусловными. Они Устанавливается только для определенных типов моделей. Модель оснащена Trend Dan В связи с этим они могут вызвать проблемы так же, как если бы Анализ наименьших квадратов.

Третий Следует предположить, что случайный член имеет определенную асимметрию Распределение глазного дна, обычно нормальное распределение. Это предположение не является необходимым при использовании OLS для классов SIC модель линейной регрессии (это Test).

В-четвертых, оценка МВФ занимает слишком много времени Время исследователь и компьютер. Оценки часто угадываются Это решения одновременных уравнений с использованием итерации. Процедуры не могут быть выражены в виде явных математических выражений Ких выражение.

Четвертый аргумент в пользу использования ММП возможен уже давно Но единственное существенное препятствие для его широкого распространения Ния, Ван Проблема быстро упрощается и компьютер стоит Оценки MMP активно интегрированы в статистический пакет.

Пример оценки МВФ автокорреляции в первичной модели авторегрессии С. Бич и Дж. Маккиннон (Бич, Маккиннон, 1978) в настоящее время является стандартным аксессуаром для статистических пакетов. Дж. Крамер (1986) До предела, этот метод является «отличной заменой линейной регрессии. Онон анализ как основной инструмент эконометрики. вероятно Он прав. Тем не менее, оценки MMP и MNC совпадают (однако, Оценка o *) В условиях Гаусса – Маркова MNE продолжает быть отправной точкой для вводных курсов по эконометрике.

Смотрите также:

• Решение задач по эконометрике

Идентификация относительно стабильных зависимостей	Спецификация модели
Величина смещения оценки для одновременных уравнений	Послесловие к функциям спроса