Оглавление:
Обоснование последовательности расчета
На рисунке 3.45. представлена сложная электрическая цепь, в которой заданы величины всех ЭДС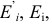 
источников тока 
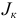и резисторов 
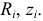. Необходимо выполнить расчет величин токов в ветвях электрической цепи.
На первом этапе необходимо проставить произвольное направление токов в ветвях и упростить электрическую цепь, по известным методам, пронумеровав узлы. На рисунке 3.46. представлена упрощенная цепь, где
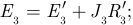
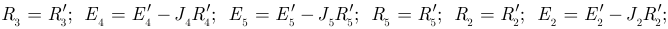
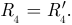
Положительные направления результирующих ЭДС в ветвях выбираются произвольно и в данном примере выбраны совпадающими с электрической цепью на рисунке 3.39.
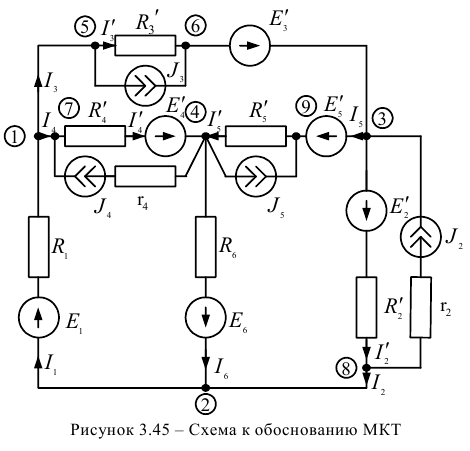
Воспользуемся для обоснования метода MKT методом непосредственного применения законов Кирхгофа и составим по первому закону Кирхгофа (к — 1) уравнений (т. е. 4 — 1 = 3) для узлов 1,2,3 и по второму закону Кирхгофа для контуров, I, II, III:
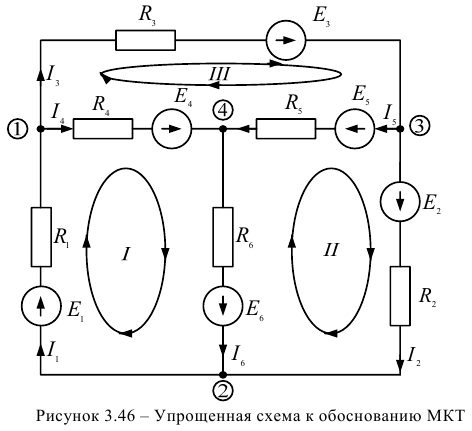
Ветви 4, 5 и 6 — ветви дерева (рисунок 3.40.), а ветви 1, 2 и 3 — ветви соединения. Токи ветвей соединения называют контурными токами и обозначают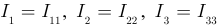 
Выразим токи ветвей дерева через контурные токи из уравнений (3.38):
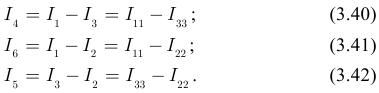
Исключаем токи смежных ветвей (дерева) из системы уравнений (3.39), для чего выражения для токов (3.40) — (3.42) подставим в уравнения (3.39):
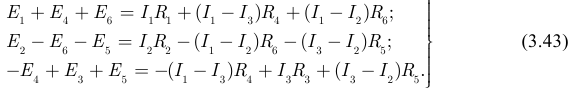
Выполним группировку коэффициентов при контурных токах уравнений системы (3.43) и получим стандартную форму системы уравнений по MKT:
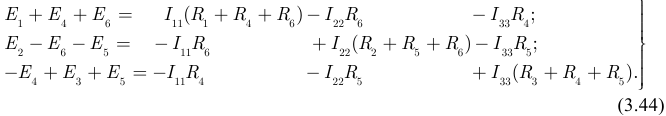
Анализ системы уравнений (3.44) позволяет прийти к следующим выводам:
- коэффициент при контурном токе, номер которого совпадает с номером контура, для которого составлено уравнение, равняется арифметической сумме сопротивлений этого контура, ее мы будем называть собственным сопротивлением контура
:
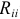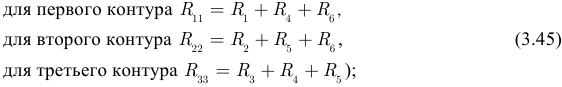
- коэффициенты
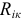при контурных токах, номера которых не совпадают с номером контура, для которого составляется уравнение, являются сопротивлениями ветвей, которые принадлежат одновременно двум контурам; знак этих коэффициентов зависит от того, одинаково или противоположно направлены токи в этих ветвях, и мы будем называть их взаимными сопротивлениями контуров
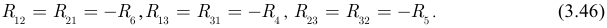
Левые части уравнений (3.44) являются алгебраическими суммами источников ЭДС по второму закону Кирхгофа и мы будем называть их контурными
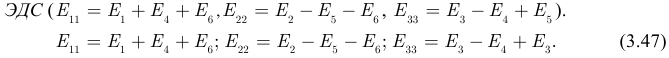
Группировка коэффициентов в правых частях уравнений (3.44) приведет к системе уравнений (3.48):
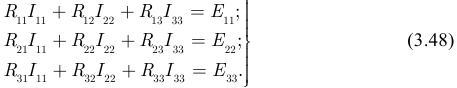
Система уравнений может быть решена с помощью определителей:
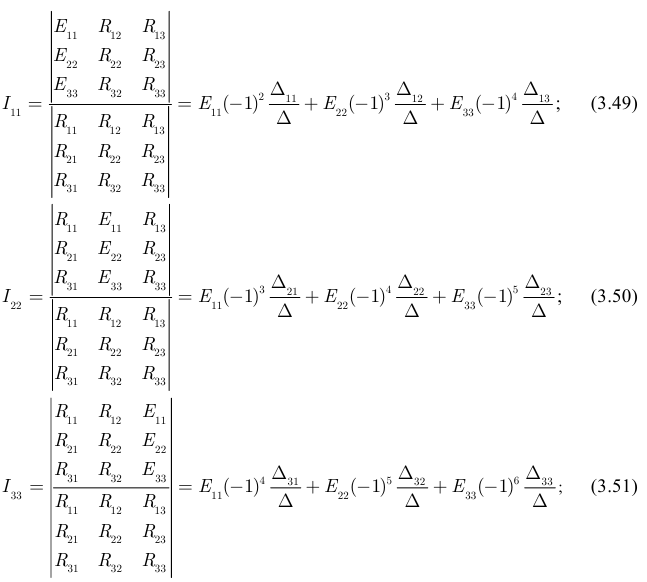
где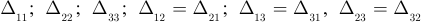 
— алгебраические дополнения формул.
Система уравнений (3.48) является стандартной формой записи уравнений по методу контурных токов для любой электрической цени с
тремя независимыми контурами. Учитывая, что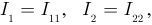 
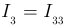можно рассчитать остальные токи по формулам (3.40) — (3.42).
Можно сформулировать правило:
Ток в любой ветви равен алгебраической сумме контурных токов в этой ветви, при этом положительный знак выбирают при совпадении направления контурного тока с направлением тока ветви, и отрицательный — наоборот. Расчет остальных токов выполним по схеме (рисунок 3.45).
Для узла 5 по первому закону Кирхгофа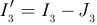 
. Аналогично для узла 1 
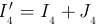; для узла 9 
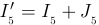; для узла 8 
.
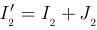Если количество независимых контуров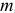 
, система уравнений по методу контурных токов будет иметь вид:
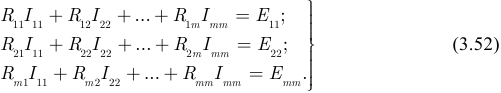
В матричной форме систему (3.52) можно записать в полном виде:
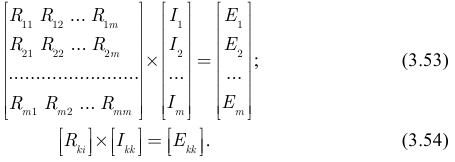
где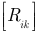 
— квадратичная матрица собственных и взаимных сопротивлений контуров или кратко — матрица сопротивлений; 
— матрица-столбец контурных ЭДС; 
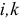— соответственно номера рядка и столбца элементов матриц.
Матрица сопротивлений симметричная, так как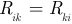 
. На главной диагонали этой матрицы расположены собственные сопротивлении контуров 
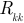. Решение матричных уравнений (3.53) и (3.54) относительно неизвестной матрицы контурных токов имеет вид:
где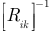 
— обратная матрица сопротивлений.
Последовательность расчёта по методу контурных токов
Расчет цепей по методу контурных токов рекомендуется вести в следующей последовательности.
- Упростить исходную цепь, заменив реальные источники тока на реальные источники напряжения.
- Выбрать независимые контуры, направление контурных токов в них и направления токов в ветвях, входящих только в один контур должны совпадать с направлением контурного тока.
- Записать и решить стандартную систему уравнений по методу контурных токов.
- По найденным контурным токам найти по первому закону Кирхгофа токи в остальных ветвях схемы.
- Выполнить проверку результатов расчёта.
Если в схеме идеальные источники тока и их не преобразовали в модели с источниками ЭДС, расчет имеет ряд особенностей. Чтобы выбрать независимые контуры, необходимо использовать дерево графа так, чтобы в идеальные источники тока входили в ветви соединения. В этом случае токи источников тока приравниваем к известным контурным токам, а уравления составляют и решают только для контуров с неизвестными контурными токами. При этом в уравнения включаются слагаемые, которые приравняли токам идеальных источников тока.
Задача 3.9.
Для электрической цепи, схема которой изображена на рисунке 3.47. выполнить расчёт токов в ветвях электрической цепи, если параметры элементов имеют следующие значения:
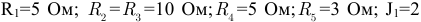
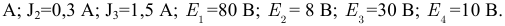
Решение:
На первом этапе упростим схему рисунка 3.47, заменив модели источников энергии с источниками тока на модели с источниками ЭДС. Так заменяем: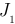 
и 
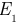на эквивалентные источники ЭДС
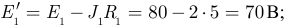
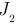и 
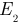на эквивалентный источник
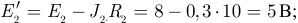
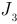и 
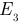на
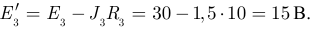
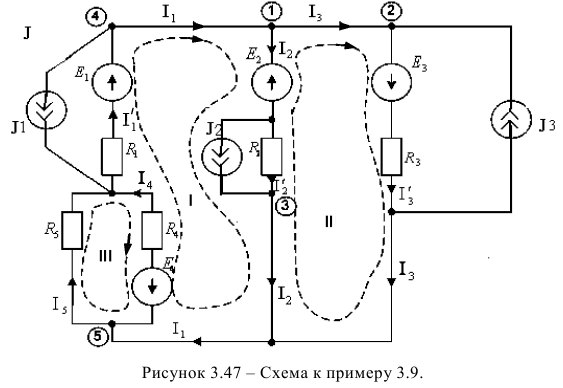
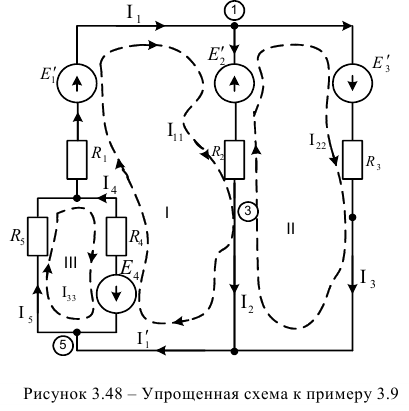
На втором этапе выбираем положительные направления токов в ветвях схемы с неизвестными контурными токами и произвольно выбираем положительные их направления (рисунок 3.48).
На третьем этапе составляем стандартную систему уравнений по MKT для трёх неизвестных контурных токов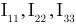 
:
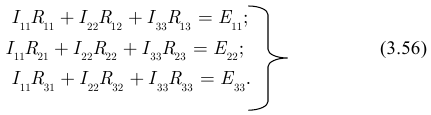
Здесь:
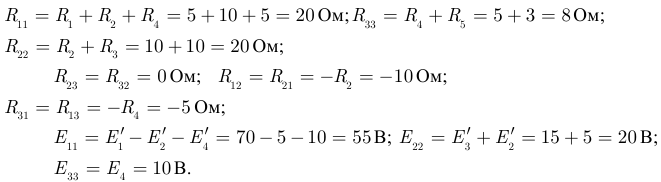
Подставляем полученные значения коэффициентов в уравнения системы (3.56) получаем:
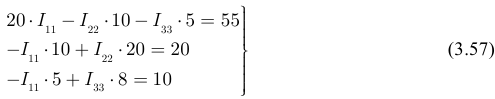
Решаем полученную систему уравнений с помощью определителей:
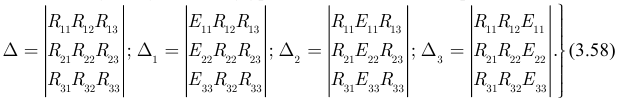
Правила вычисления определителей при раскрытии по первому столбцу:
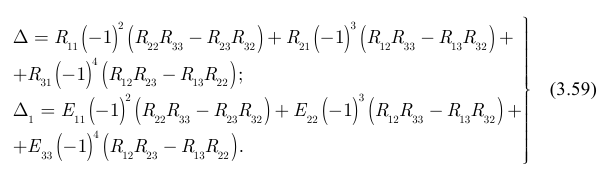
На четвёртом этапе вычисляем токи ветвей:
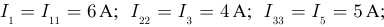
Ток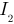 
, вычисляем для узла 1 по первому закону Кирхгофа:
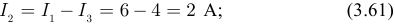
Аналогично величины токов:
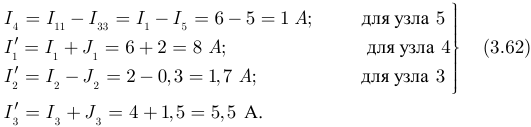
На пятом этапе выполняем проверку вычислений подстановкой величин токов в уравнения, составленные по второму закону Кирхгофа для исходной схемы рисунка 3.47:
Подставляем заданные параметры элементов электрической цепи и величины токов в систему уравнений (3.63):
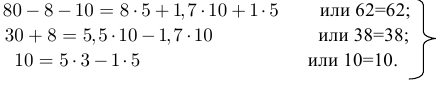
Система уравнений (3.63) превратилась в верное равенство.
Эта страница взята со страницы задач по электротехнике:
Электротехника — решения задач и примеры выполнения заданий
Возможно эти страницы вам будут полезны:
