Оглавление:
Метод кинетостатики
Допустим, что к несвободной материальной точке массы т приложена некоторая активная сила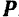 
.
Освобождая мысленно точку от связей, заменим их действие па тело реакцией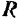 
этих связей. Тогда точку 
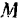можно считать свободной, но находящейся под действием силы 
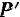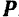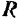, являющейся равнодействующей сил и (рис.’ 228).
По основному уравнению динамики точки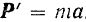 
Условно приложим к точке еще и вектор
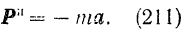
Вектор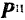 
равный по модулю произведению массы точки на модуль ее ускорения и направленный в сторону, противоположную ускорению точки, называют силой инерции этой точки.
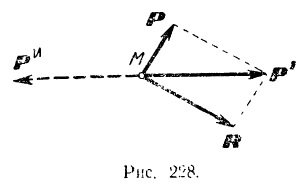
Геометрическая сумма сил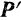 
и 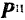или, что все равно (рис. 228), геометрическая сумма сил 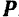, 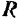и 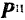равна, очевидно, нулю, и эта совокупность сил формально представляет уравновешенную систему сходящихся сил.
Если материальная точка в результате взаимодействия с другими окружающими ее телами приобрела ускорение а, то к этим телам согласно третьему закону динамики приложены со стороны точки силы противодействия. Геометрическая сумма этих сил, приложенных, вообще говоря, к различным телам, формально равна — та, т. е. равна силе инерции точки.
Реально существуют лишь составляющие силы инерции материальной точки, приложенные не к этой точке, а к тем телам, которые являются источниками действующих на нее активных сил, и к связям, наложенным на точку. Однако условное присоединение силы инерции точки к числу сил, в действительности к ней приложенных, формально позволяет применить к решению задач динамики хорошо известные приемы статики и лежит в основе метода, называемого методом кинетостатики.
Идея метода кинетостатики может быть сформулирована следующим образом: во всякий момент движения материальной точки совокупность приложенных к точке активных сил, реакций наложенных на точку связей и силы инерции данной точки (условно приложенной к ней самой) удовлетворяет условию равновесия системы сходящихся сил.
Метод кинетостатики легко распространить и на материальную систему.
Представим себе находящуюся в движении систему, состоящую из ряда связанных между собой по какому-либо определенному закону материальных точек. Во всякий момент движения системы приложенные к любой ее точке активные силы, реакции связей и сила инерции этой точки (условно приложенная к ней самой) формально удовлетворяют условию равновесия. Отсюда следует, что формально удовлетворяет условиям равновесия и вся совокупность сил, состоящая из приложенных к системе активных сил, реакций связей и сил инерции всех точек системы. Следовательно, во всякий момент движения системы материальных точек совокупность приложенных к ним активных сил, реакций связей и условно приложенных к каждой точке системы сил инерции этих точек удовлетворяет соответствующим условиям равновесия.
При криволинейном движении точки 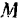(рис. 229) ее силу 
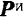инерции можно разложить на две составляющие: касательную (тангенциальную) силу инерции 
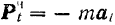, направленную противоположно касательному 
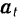, ускорению точки, и нормальную (центробежную) силу инерции 
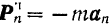, направленную противоположно нормальному ускорению точки.
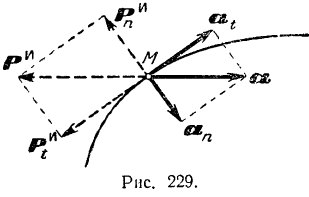
Так как нормальное ускорение направлено по нормали к траектории в сторону ее вогнутости, то центробежная сила инерции направлена по нормали в сторону выпуклости, т. е. по нормали от центра кривизны. Последним и объясняется название этой силы.
При решении задач динамики системы методом кинетостатики часто приходится определять сумму моментов сил инерции точек вращающегося твердого тела относительно его оси вращения.
Разложим силу инерции каждой точки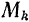 
тела, вращающегося вокруг неподвижной оси 
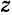(рис. 230), на нормальную (центробежную) силу 
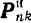инерции и тангенциальную силу 
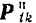инерции, направленные противоположно нормальному и тангенциальному ускорениям точки.
Так как линии действия центробежных сил инерции пересекают ось вращения, то их моменты относительно оси вращения тела равны нулю.
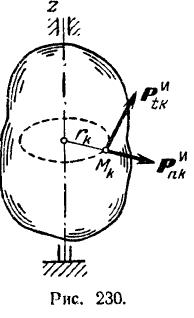
Таким образом, сумма моментов сил инерции точен-вращающегося твердого тела будет равна сумме моментов его тангенциальных сил инерции.
Найдем абсолютное значение этой суммы моментов:
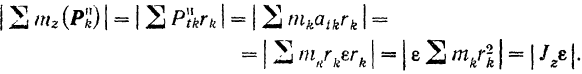
Так как тангенциальные силы инерции точек тела направлены в стороны, противоположные их тангенциальным ускорениям, то знак момента сил инерции вращающего твердого тела будет противоположен знаку его углового ускорения.
Учитывая это, можно записать:
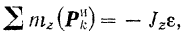
где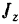 
— момент инерции тела относительно его оси вращения, 
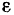— величина углового ускорения тела.
Метод кинетостатики вследствие своей простоты и наглядности широко используется в инженерной практике для решения динамических задач. Особенно удобен этот метод для определения так называемых динамических реакций связей, т. е. реакции, возникающих в связях при движении системы. Этим методом можно пользоваться и для определения ускорений тел, входящих в состав системы.
Вместе с этим, надо сказать, что все без исключения задачи динамики можно решать и без применения метода кинетостатики, не пользуясь вовсе понятием сил инерции.
Пример задачи:
Груз весом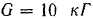 
поднимается вертикально вверх с ускорением 
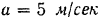при помощи нити, перекинутой через неподвижный блок (рис. 231). Определить натяжение нити.
Решение:
На груз действуют следующие силы: сила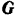 
тяжести груза, направленная вертикально вниз, и реакция 
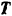нити, численно равная ее натяжению и направленная вертикально вверх. Условно присоединим к этим силам силу 
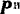инерции груза, равную по модулю 
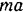и направленную противоположно ускорению, т. е. вертикально вниз. Тогда, пользуясь методом кинетостатики, можно формально применить к системе сил 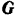, 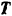и 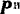условия равновесия.
Из условия равновесия сил, действующих по одной прямой, имеем;
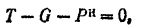
откуда
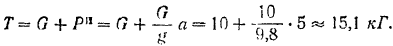
Сила 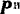груза условно приложена к самому грузу в целях применения к решению задачи метода кинетостатики. Но эта сила реальна по отношению к нити, заставляющей груз двигаться с данным ускорением вверх. При некотором ускорении натяжение 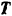нити может оказаться настолько большим, что нить оборвется.
Если бы груз опускался с ускорением, то его сила инерции была бы направлена вертикально вверх. При тех же данных мм бы имели:
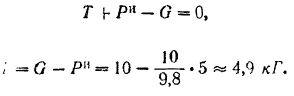
Если бы груз был только подвешен на нити или двигался бы прямолинейно и равномерно, то
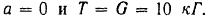
Пример задачи:
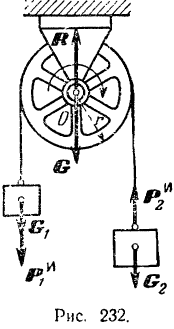
Через блок перекинута гибкая пить, к концам которой подвешены грузы (рис. 232) весом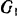 
и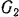 
. причем 
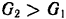. Вес блока 
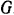, его радиус 
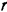Пренебрегая массой нити и принимая блок за материальную окружность, определить ускорение грузов.
Решение:
Условно присоединим к силам, действующим на систему (блок-грузы), силы инерции всех точек этой системы.
Так как 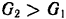, то груз 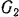будет двигаться с ускорением вниз, сообщая блоку угловое ускорение по ходу стрелки часов.
Сила инерции большего груза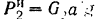 
и направлена вертикально вверх. Сила инерции меньшего груза 
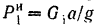и направлена вертикально вниз. Так как знак момента си i инерции вращающегося тела противоположен знаку его угловою ускорения, то по форму те (212) сумма моментов сил инерции точек блока относительно его оси:
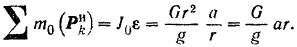
Применяя условия равновесия к совокупности действующих на систему активных сил, реакций связей и сил инерции точек системы, приравниваем нулю сумму .моментов этих сил относительно оси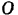 
блока:
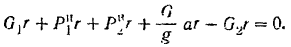
Моменты силы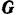 
тяжести блока и реакции 
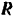его оси относительно оси 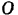блока равны кулю и потому в написанное выше равенство не входят.
Подставляя в это равенство найденные выше значения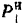 
и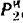 
, получим:
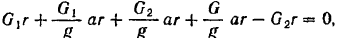
откуда находим:
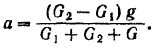
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
